Суть первого закона Кеплера заключается в том, что все планеты Солнечной системы движутся по замкнутой эллиптической кривой с Солнцем в качестве одного из фокусов.
Законы Кеплера
Взаимодействие гравитации легче наблюдать в массивных объектах с огромной массой. В нашей повседневной среде трудно наблюдать влияние гравитации между объектами, даже если эти объекты весят сотни или тысячи килограммов. В микромире силы гравитационного взаимодействия ничтожны, поэтому на первый план выходят другие взаимодействия между элементарными частицами и атомами.
Гравитация удерживает организмы и предметы на поверхности планеты и определяет, как планета движется вокруг Солнца. Гравитация определяет тот факт, что планеты удерживаются вокруг своих звезд и что спутники не могут вырваться в космос и остаются на орбите вокруг этих планет.
Закон всемирного тяготения, или так называемая теория гравитации, был открыт именно благодаря наблюдению за планетами в нашей Солнечной системе.
Наблюдая за движением небесных тел с Земли, может показаться, что все эти тела движутся по сложным орбитам. Например, древний ученый Птолемей, открывший законы планетарного движения, предложил поместить Землю в центр Вселенной, а остальные планеты и звезды движутся вокруг нее по большим и малым орбитам.
Рис. 1. 24. 1.1. условное изображение наблюдаемого движения Марса на звездном фоне.
Законы движения планет, установленные Птолемеем, не оспаривались ни одним исследователем в течение 14-го века, и только в середине 16-го века они были заменены геоцентрической теорией, согласно которой все планеты движутся вокруг Солнца.
На основе геоцентрической теории стало гораздо проще объяснить орбиты небесных тел. Основываясь на работе Коперника и наблюдениях за движением планет датским астрономом Блаэ, немецкий астроном Кеплер сформулировал три эмпирических закона движения для планет Солнечной системы.
Первый закон Кеплера
Планеты в нашей Солнечной системе вращаются по эллиптическим орбитам. На очаге одной из таких орбит находится Солнце.
Первый закон Кеплера был проиллюстрирован фотографиями. На ней изображена планета с меньшей массой, чем у звезды. Звезда находится в фокусе затмения, куда движется планета. Точка P — это орбита, ближайшая к звезде, и называется перигелием. Точка А — это орбитальная точка, наиболее удаленная от звезды, и называется пупком. Главная ось эллипса лежит между афелием и перигелием.
Рис. 1. 24. 2.2. Эллиптические орбиты планеты с массой m< < M. a – длина большой полуоси, F и F ' – фокусы орбиты.
В Солнечной системе все планеты, за исключением Плутона, движутся по почти круговым орбитам.
Второй закон Кеплера, или закон площадей
Радиус-векторы планет одинаково разнесены и представляют собой равные площади.
Рисунок 1. 24. 3.3. Закон областей — это второй закон Кеплера.
Эквивалент второго закона Кеплера можно рассматривать как закон сохранения импульса. На рисунке выше показан вектор импульса объекта p→ и его компоненты pr→ и p⊥→. Площадь ∆t, определяемая радиус-вектором в краткосрочной перспективе, приблизительно равна площади треугольника, построенного на r∆θ и высоте r:.
∆ S = 1 2 r 2 ∆θ или ∆ S ∆ t = 1 2 r 2 ∆θ ∆ t = 12r2ω; (∆ t→ 0).
где ω = ∆θ ∆ t; (∆ t→0) — угловая скорость.
Момент L имеет абсолютное значение, равное произведению коэффициентов векторов pr→ и p⊥→.
L =rp⊥=r(mv⊥)=mr2ωv⊥=rω, так как.
Эти отношения имеют место:
Таким образом, согласно второму закону Кеплера d s d t = co n s t, момент движения остается неизменным.
В частности, поскольку скорости планет в Перилио v p→ и Афинах v a→ направлены перпендикулярно радиус-векторам r p→ и r a→:.
В законах Кеплера были относительно небольшие ошибки, но они все равно были эмпирическими. Не было никакой теоретической базы. Позднее эта проблема была решена Исааком Ньютоном, который в 1682 году открыл всемирный закон всемирного тяготения.
Первый закон Кеплера
Кеплер заметил, что наблюдения Брея противоречат идее кругового движения планет вокруг Солнца. Это было особенно верно для Марса, орбита которого, согласно наблюдениям Дейна, не могла представлять собой идеальный круг. Браге обнаружил, что его расчеты были очень точными, и его последователи не сомневались в их правильности.
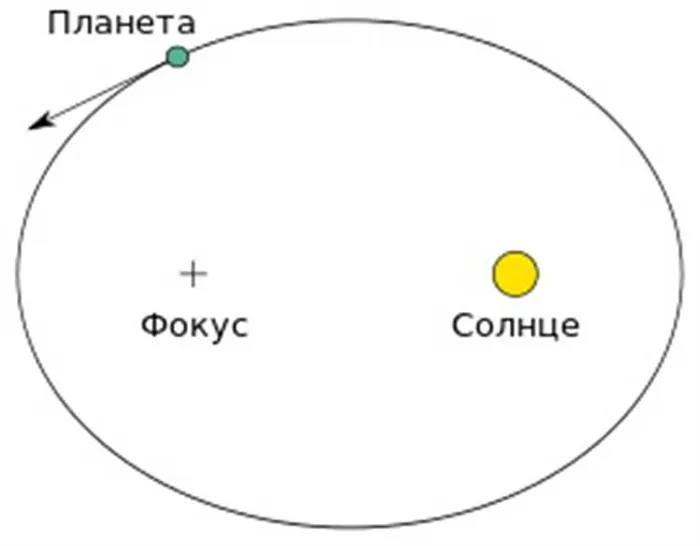
Позднее немецкие математики посчитали, что орбиты не имеют двух фокусных точек. Это условные точки, выбранные так, чтобы сумма расстояний от них до каждой точки отсутствия была постоянной величиной. В случае с эллиптическими орбитами одной из фокусных точек является Солнце.
Форма недостатка вычисляется по причине фокусного расстояния до полуоси трека. Полученное значение представляет собой эксцентриситет дорожки. Если ноль, то орбита является полным циклом, ноль и один отличаются по элонгации, а один или несколько являются притчами.
Второй закон Кеплера
Если орбита короткая, как движется объект? На каких участках орбитального маршрута он ускоряется и замедляется?
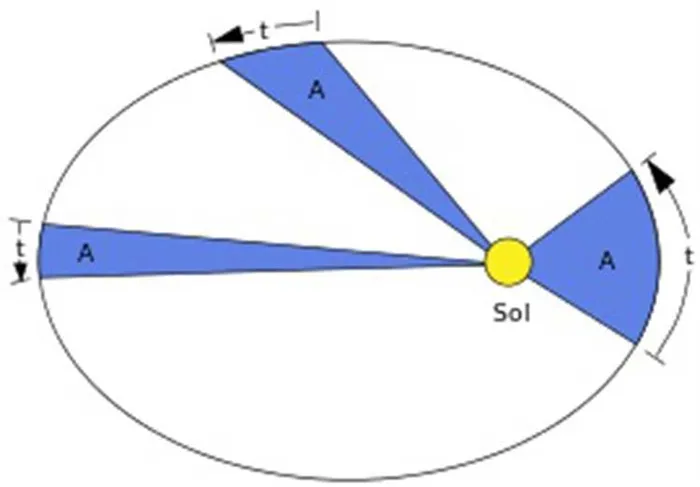
Немецкие ученые обнаружили, что если взять две части орбитального маршрута, то площадь получившегося образования будет одинаковой, поскольку планета проходит через Солнечную систему через равные промежутки времени и через расчетный радиус-вектор от ее края до центральной звезды. Это упрощенное изложение второго закона.
Чтобы поддерживать стабильность области, тело должно двигаться с разной скоростью в разных частях своей орбиты. Так, например, Земля до ближайшего к Солнцу подхода движется быстрее, чем дальше от Солнца.
Третий закон Кеплера
Третье направление движения тел в Солнечной системе относится исключительно к понятиям пери и афелий. Проведя между ними условную линию, можно определить главные оси орбит планет. Таким образом, половина этого участка является полуосевой.
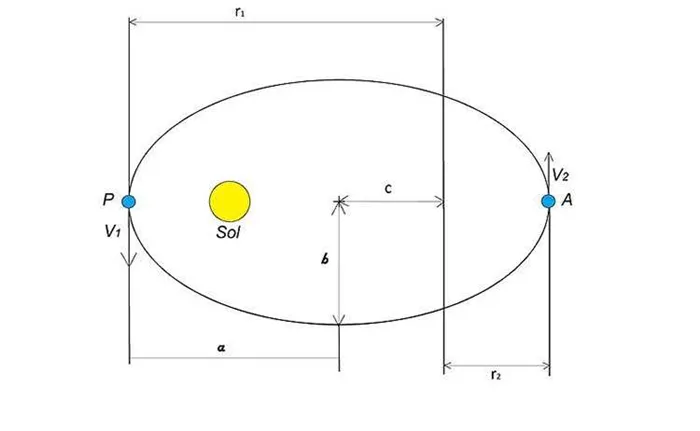
Из наблюдений Кеплер сделал вывод, что отношение полного вращения вокруг центральной звезды двух планет в квадратной системе всегда равно полуоси орбит этих тел и полуоси квадрата.
Сложность в доказательстве и принятии трех законов заключалась в том, что они оказались эмпирическими. Однако в конце XVII века Ньютон открыл классическую теорию гравитации. Она помогла продемонстрировать правильность кризиса немецкого астронома и объяснила движение планет вдоль недостатка Солнца. Помимо массы объекта и его расстояния от звезды, Ньютон обнаружил, что другие свойства не влияют на притяжение гравитации.
Ньютон также изменил третий вклад Кеплера. Он обнаружил, что для соблюдения соотношения необходимо учитывать массу космического объекта. Такая интерпретация третьего закона помогает определить массу планеты или спутника, зная его орбиту и размер орбиты.
Законы Иоганна Кеплера помогли определить форму планетарных орбит и рассчитать период вращения планеты, ее скорость и то, как она меняется по мере приближения и удаления от Солнца. Ученые вывели Землю из классификации особых астрономических объектов в системе и обнаружили, что, как и другие планеты в нашей звездной системе, она подчиняется всем трем законам.
По этим законам можно вычислить продолжительность года (время полного оборота вокруг Солнца) для любой планеты, если она известна с Солнца.
Второй закон Кеплера (закон площадей)
Радиус-векторы планет описывают равные площади с равными интервалами.
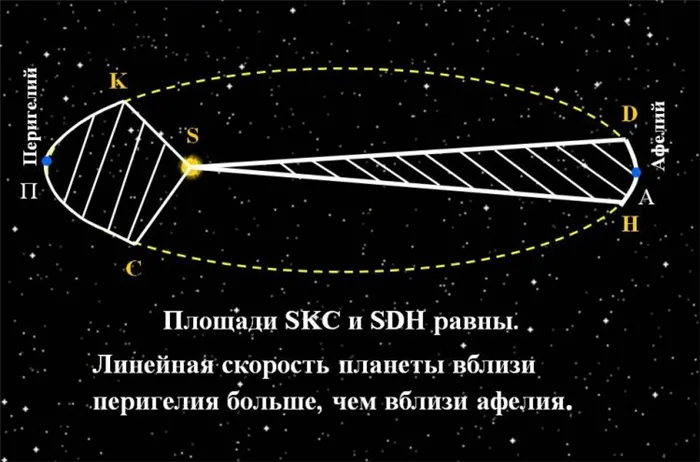
Второй закон Кеплера определяет, что Все планеты движутся на уровне, проходящем через центр Солнца. В то же время радиус-вектор и его планеты, соединяющиеся с Солнцем, представляют собой равные области. Поэтому ясно, что тело движется вокруг желтого карлика неравномерно, с максимальной скоростью перилиума и минимальной скоростью обфейни.
Фактически, это видно из движения Земли. Каждый год в начале января наша планета ускоряет свое движение во время транзита из перильца. По этой причине движение Солнца по эклиптике происходит быстрее, чем в другое время года. В начале июля Земля проходит через Дезир, а Солнце медленно движется по эклиптике.
Третий закон Кеплера (гармонический закон)
Квадрат орбитального периода планеты называется орбитальным кубом.
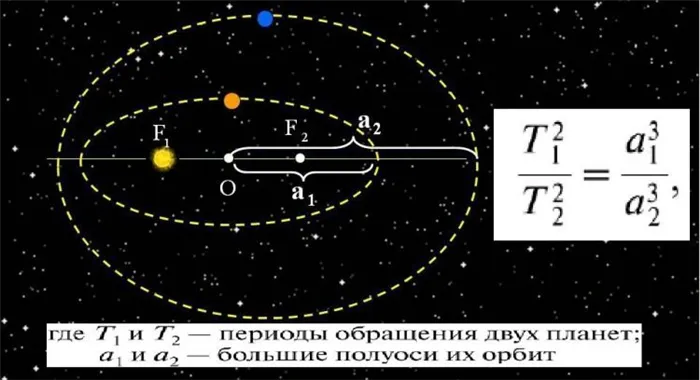
Согласно третьему закону Кеплера, между периодом планеты и ее средним расстоянием от яркого тела возникает зависимость. Третий закон Кеплера выполняется как для планет, так и для спутников, с ошибками, не превышающими 1%.
Этот закон позволяет вычислить период одного года (полное время вращения вокруг Солнца) для любой планеты, если он известен по Солнцу. И наоборот, этот же закон позволяет вычислять орбиты, зная период вращения.
Дальнейшее развитие
В законах Кеплера были относительно небольшие ошибки, но они все равно были эмпирическими. Не было никакой теоретической базы. Позднее эта проблема была решена Исааком Ньютоном, который в 1682 году открыл всемирный закон всемирного тяготения.
Закон Кеплера стал важным шагом в понимании и объяснении движения планет.
Чтобы поддерживать стабильность в какой-либо области, небесные тела должны двигаться в разных частях своих орбит с разными скоростями. Например, наша Земля движется вокруг Солнца неравномерно. В перионах линейная скорость больше, чем в аффинах.
Третий закон Кеплера
Каждая орбита планеты имеет ближайшую к Солнцу точку, называемую перицентром. Точка трека над Солнцем называется наивной. Отрезок, соединяющий эти две точки, называется большой осью пути. Разделив этот отрезок посередине, можно получить полуось, наиболее часто используемую в астрономии.
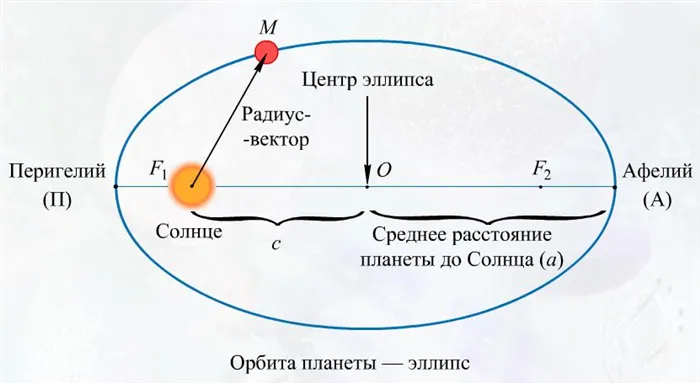
Основание для отсутствия
Третий закон Кеплера, касающийся движения планет, звучит следующим образом
Квадрат орбиты планеты вокруг Солнца до полуоси этой планеты стабилен и эквивалентен квадрату орбиты другой планеты вокруг Солнца. Эта планета.
Также может быть зафиксировано другое соотношение.
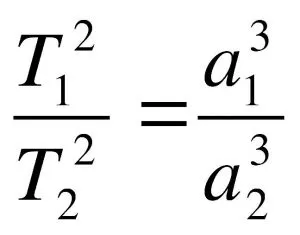
Одно из произведений Третьего закона.
Существует прямая связь между периметром и AFELI. Отрезок, соединяющий эти две точки, называется большой осью пути. Разделив этот отрезок посередине, можно получить полуось, наиболее часто используемую в астрономии.
Третий закон
Квадрат времени одной орбиты пропорционален кубическому параметру среднего расстояния самой планеты от Солнца. У этой теории есть и другое название: эту аксиому часто называют законом гармонии. В этом случае проводится сравнение между временной частью орбиты и радиусом планетарной орбиты. Таким образом, для каждой планеты отношение квадратичной экспоненты периода движения к среднему расстоянию от светила до кубического тела аналогично.
Немецкий ученый Иоганн Кеплер был первооткрывателем законов движения планет вокруг Солнца. Эти аксиомы помогли определить форму орбитального пути, позволили рассчитать орбитальные периоды и скорости и наблюдать за изменениями экспоненты скорости в точках приближения к Солнцу и удаления от него. Ученые доказали, что Земля, как и все остальные планеты Солнечной системы, вращается вокруг Солнца согласно всем трем теориям, без исключения.
На этой диаграмме показаны две орбиты небесного тела, движущегося вокруг звезды. Одна из орбит круговая с радиусом R, а другая — эллиптическая с осью α. Если R = a, то, согласно третьему закону Кеплера, периоды обращения планет на таких орбитах равны.
Первый закон Кеплера
Иоганн Кеплер, немецкий математик и астроном, живший в XVII веке, посвятил себя изучению Солнечной системы. Изучая научные работы Коперника и Браге, он заметил неточности в описании орбит планет и обнаружил, что орбиты некоторых планет не следуют идеальным периодам. Он усовершенствовал все имевшиеся на тот момент знания и обобщил законы движения планет в Солнечной системе.
В ходе своих длительных наблюдений Кеплер обнаружил, что орбиты всех планет нашей системы находятся примерно на одном уровне. Большинство тел вращаются по кругу. Только две планеты, Марс и Плутон, движутся вокруг Солнца по более длинным орбитам.
Суть первого закона Кеплера заключается в том, что все планеты Солнечной системы движутся по замкнутой эллиптической кривой с Солнцем в качестве одного из фокусов.
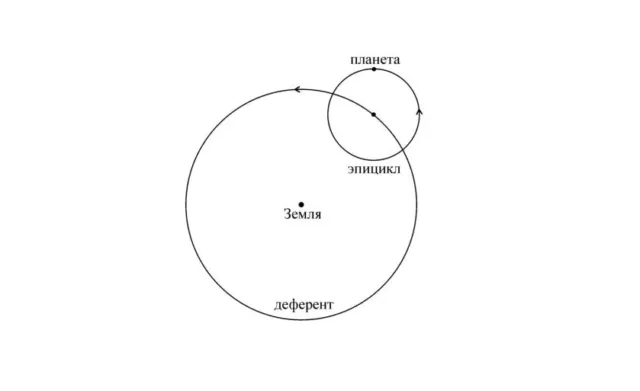
Рисунок 1. Планетарные круги.
Есть только две центральные точки. Это две точки кривой, и общее расстояние от них до любой точки эллипса постоянно.
Форма орбиты, очерчиваемой объектом, зависит от его скорости. При заданной скорости тело очерчивает круг вокруг своего центра тяжести. Эта скорость называется начальной космической скоростью и придается объектам, запускаемым в качестве спутников. Она составляет приблизительно 8 км/с.
Второй закон Кеплера
Обнаружив, что орбиты планет несовершенны, ученые решили выяснить, в какой части орбиты тела замедляются и ускоряются.
Второй закон Кеплера гласит, что каждая планета движется в плоскости, проходящей через центр Солнца, и что вектор лучей света соединяет Солнце и планеты на равных расстояниях и равных площадях.
Есть две концепции, связанные со вторым законом Кеплера, которые применимы к Солнечной системе.
Чтобы поддерживать стабильность в какой-либо области, небесные тела должны двигаться в разных частях своих орбит с разными скоростями. Например, наша Земля движется вокруг Солнца неравномерно. В перионах линейная скорость больше, чем в аффинах.
Третий закон Кеплера
Существует прямая связь между периметром и AFELI. Отрезок, соединяющий эти две точки, называется большой осью пути. Разделив этот отрезок посередине, можно получить полуось, наиболее часто используемую в астрономии.
Третий закон Кеплера звучит следующим образом. Отношение суммарных оборотов вокруг центральной звезды двух квадратных планет в системе всегда равно отношению орбитальных путей этих кубов.
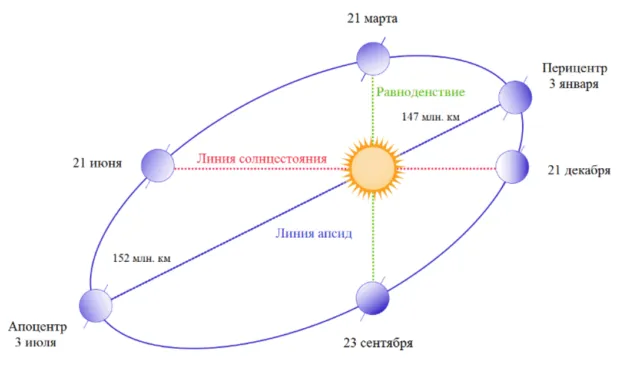
Рисунок 3.Орбиты движения Земли вокруг Солнца.
Этот закон позволяет рассчитать продолжительность года планеты, зная ее расстояние от Солнца. И наоборот, этот закон позволяет вычислить орбиту, зная период вращения.
Третий закон Кеплера выполняется как для планет, так и для спутников, и его ошибка не превышает 1%.
На выставке по географии в пятом классе важно объяснить основные три закона Кеплера о движении планет в Солнечной системе.
Немецкие ученые обнаружили, что если взять две части орбитального маршрута, то площадь получившегося образования будет одинаковой, поскольку планета проходит через Солнечную систему через равные промежутки времени и через расчетный радиус-вектор от ее края до центральной звезды. Это упрощенное изложение второго закона.
Третий закон Кеплера
Квадрат орбитального периода планеты называется орбитальным кубом.
Согласно третьему закону Кеплера, существует зависимость между периодом обращения планеты вокруг Солнца и полуосью ее орбиты. Этот закон выполняется как для планет, так и для спутников и имеет погрешность менее 1%.
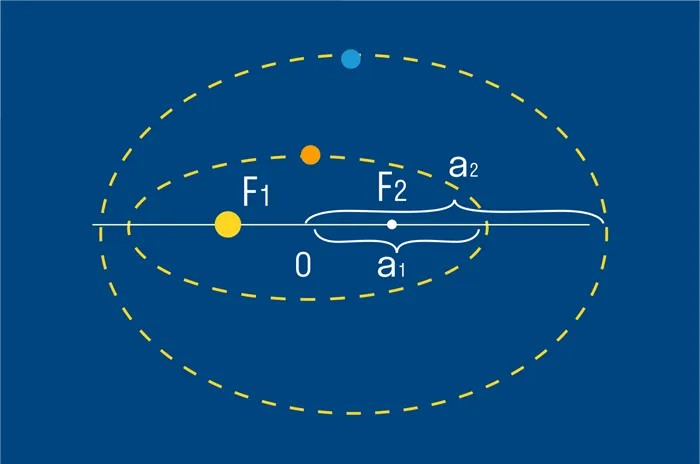
Третий закон Кеплера
Количество планет с той же орбитальной осью, что и у Солнца, которое определяется t1 и t2 — Орбитальные периоды двух планет c
a1 и один2 — Полуось орбиты планеты.
По этим законам можно вычислить продолжительность года (время полного оборота вокруг Солнца) для любой планеты, если она известна с Солнца.
Можно выполнить и обратное действие. Другими словами, орбиты можно вычислить, зная орбитальный период.
Закон всемирного тяготения
Законы Кеплера являются результатом наблюдений и обобщений. Они лежат в основе закона всемирного тяготения, который гласит, что все тела притягиваются друг к другу. Общая сила тяжести прямо пропорциональна массе тела и обратно пропорциональна ее квадрату.
В соответствии с этим законом видами тяжести являются
Закон всемирного тяготения
F — гравитационная сила n
M — масса первого тела (часто планеты) кг
M — масса второго тела кг
R — расстояние b между двумя b.
G — гравитационная постоянная
g = 6,67-10 -11 м 3 -кг -1 -с -2
Ньютон был первым, кто пришел к выводу, что между всеми телами в пространстве существует сила притяжения и что эти силы определяют характер движения этих тел.
Первая и вторая космические скорости
Законы Кеплера применимы не только к движению планет и других тел в нашей Солнечной системе, но и к движению спутников и космических кораблей. В этом случае центром тяжести является Земля.
В серии книг Дугласа Адамса «Галактический выдр» говорится, что летать — значит просто потерять Землю. Чтобы обогнать Землю и стать спутником, необходимо достичь начальной космической скорости 7,9 км/с. Послушайте, как это происходит:.
Спутники Земли — это космические аппараты, вращающиеся вокруг Земли по орбите, центрированной на Земле. Для этого транспортному средству необходима начальная скорость, превышающая первую космическую скорость.
Начальная космическая скорость
v1 — Начальная космическая скорость м/с
G — ускорение силы тяжести конкретной планеты м/с 2
R — радиус планеты m
На планете Земля G ≈ 10 м/с 2.
Существуют также вторая и третья космические скорости. Вторая космическая скорость — это скорость, необходимая для создания лодки-спутника Солнца, а третья — скорость, необходимая для выброса лодки за пределы Солнечной системы.
Вторая космическая скорость
v2 -это вторая космическая скорость, м/с.
G — ускорение силы тяжести конкретной планеты м/с 2








