Сегодня на этом уроке вы вспомните величины, изученные на предыдущем уроке, решите задачи на движение и запишите свои ответы на листе самооценки.
Формула скорости — обозначение, единицы измерения и примеры нахождения
: продолжают формировать идеи новых размеров «скорости, времени и расстояния» и единиц их измерения.
- Создать условия для осознания детьми зависимости между величинами, характеризующими движение тел — скоростью, временем и расстоянием.
- Познакомить детей с понятием скорости и единицами её измерения.
- Отрабатывать вычислительные навыки, обучать детей работе с графическими моделями.
- Развивать познавательную активность детей, способности к самооценке и самоконтролю, формировать коммуникативные умения.
: карточки, карточки для работы в парах, интерактивная доска, названия единиц времени на карточках, рабочие тетради, компьютер, проектор, монитор, книги.
Закрепление и развитие знаний и умений: формы познавательной деятельности учащихся.
Формы познавательной деятельности учащихся на уроке, индивидуальная и парная работа.
Планируемые результаты работы учащихся на уроке:.
- знать понятие скорости, времени и расстоянии как новой единицы измерения, уметь решать задачи на нахождение скорости движения по известным расстоянию и времени движения;
- закрепить табличные и внетабличные случаи умножения и деления, знание единиц длины и времени.
Как обозначается скорость света и звука
Ученые доказали, что скорость света — это абсолютная величина, с которой могут перемещаться информация и энергия. Она стабильна и соответствует 299 792 458 ± 1,2 м/с. Его символом является латинская буква c.
Скорость звука зависит от плотности и упругости среды, через которую передаются звуковые волны. Измерено при числе Маха. Например, скорость ультразвука составляет от 1,2 Маха до 5 Махов. Все, что выше этого значения, называется ультразвуковой скоростью.
Очевидно, что символ, используемый для обозначения скорости, зависит от математического или физического смысла этого понятия.
Как решить проблемы с транспортом? Уравнения, связывающие скорость, время и расстояние. Проблема и решение.

Угловая скорость
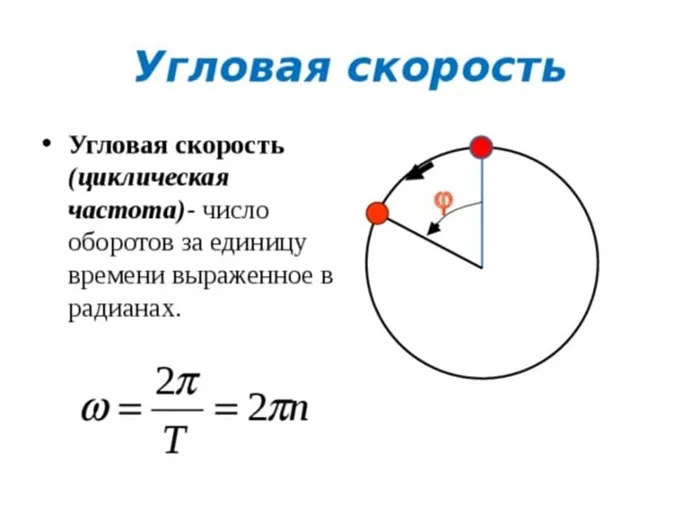
Возникает при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитываемым при его открытии, является угол поворота (f). Все основные угловые движения являются векторами. Нормальное вращение равно углу поворота df объекта за короткое время dt в направлении, противоположном движению часовой стрелки.
В математике уравнение для нахождения углового параметра записывается как w = df/dt. Угловая скорость — это осевая величина, расположенная вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, т.е. движение, при котором поворот происходит на один и тот же угол, называется равномерным. Измерение угловой скорости определяется следующим уравнением: w = f / t, где f — угол поворота, а t — время, в которое произошел поворот. Поскольку Δf = 2p, уравнение можно перефразировать в w = 2p / T. Другими словами, используется точка.
Существует зависимость между угловой скоростью и количеством оборотов: w = 2 * p*v. Это понятие используется для решения задач при описании неравномерных вращений. Существует также уравнение, связывающее линейную скорость с угловой: v = w* R, где R — компонент, отложенный перпендикулярно вектору радиусов. В качестве единицы измерения используется радиус, деленный на секунды (рад/с).
Например, определите угловую скорость преобразователя, когда подвешенная масса перемещается на 10 метров. Радиус руки равен 40 см. В первый момент подвеска неподвижна, а затем начинает опускаться с ускорением A = 0,04 м/с2 .
Поскольку линейная скорость преобразователя совпадает с линейным движением груза, мы можем написать V = (2 * a * S)½. Ответ: V = (4 * 0,04 * 10) ½ = 1,26 м/с. Угловая скорость находится по следующему уравнению: w = v/ R, R = 40 см = 0,4 м, поэтому w = 1,26 / 0,4 = 3,15 рад/с.
По сути, среднее значение — это среднее арифметическое всех скоростей, если точка движется в течение одного и того же времени. В противном случае определяемое значение является средневзвешенным арифметическим.
Кинематика — описание
Кинематика — это область инженерии, целью которой является изучение механического движения тела, игнорируя причины этого движения.
Машиностроение — это научная область физики, которая занимается изучением механического движения тел. Основной задачей этой области является определение точного положения тела в пространстве в любой момент времени. Важным понятием в этой отрасли является ключевая точка формы тела с определенной массой и размерами, которой можно пренебречь для решения задач при следующих условиях
- Путь, который преодолевает тело, существенно больше, чем его размеры.
- Расстояние между телами значительно превышает их размеры.
- Объект совершает поступательное движение.
Движение тела исследуется с помощью системы отсчета, состоящей из системы координат и прибора для измерения времени. Траектория — это линия, описывающая объект при его движении. Маршрут определяется как длина траектории в размерах шага. Смещение — это вектор, соединяющий исходное и конечное положение тела, покрытого за определенный период времени.
При движении тело увеличивает пройденное расстояние, при этом смещение увеличивается или уменьшается. Например, смещение уменьшается при обратном движении тела. Если объект движется прямолинейно в одном направлении, маршрут определяется измерением смещения. В случае криволинейного движения путь длиннее, чем перемещение. Если изучается замкнутая траектория, то смещение равно нулю.
Теория и формулы
Благодаря многолетним исследованиям в области кинематики ученые смогли вывести определенные закономерности движения тела. Используя только уравнения, можно ответить на многие вопросы, касающиеся различных свойств, которые изменяются или остаются неизменными при движении объекта.
Путь, время, скорость
Расстояние — это расстояние от одной точки тела до другой. Тело проходит путь. Это важная характеристика механического механизма. Латинская буква s является наиболее распространенным обозначением пути. Большие расстояния измеряются в метрах и километрах.
Скорость — это расстояние, которое проходит тело за единицу времени. Часто используются такие единицы измерения времени, как часы, минуты и секунды. Для расчета скорости определяется причина расстояния, которое проходит за время. Если расстояние измеряется в метрах, а время движения — в секундах, то скорость должна быть рассчитана в метрах в секунду (м/с). Латинская буква ɑ (v ɑ ɑ) используется для обозначения скорости.
Во многих случаях необходимо определить время поездки. Это обозначается латинской буквой ɑ (t \).
Важно отметить, что скорость, маршрут и время взаимосвязаны. Если известны характеристики скорости и времени, можно определить пройденное расстояние. Маршрут в этом случае равен произведению скорости и времени, рассчитанного по типу.
При известных значениях времени и расстояния очень легко определить скорость движения тела по следующему уравнению
Равномерное движение
Равномерные движения — это движения тела, которые совершают равные перемещения за равные промежутки времени.

Скорость равномерного движения определяется как причина движения вплоть до периода, в течение которого выполняется движение. Уравнение имеет следующие формы
Для отображения вектора скорости на оси OX уравнение имеет следующий вид
Если вектор скорости отображается на координатной оси, то он равен скорости изменения данной координаты.
Прямолинейное равноускоренное движение
Равномерно ускоренное движение — это движение по линейной траектории, характеризующееся постоянным ускорением.
Ускорение линейного равномерно ускоренного движения представляется следующим образом.
Это движение показывает увеличение или уменьшение скорости. Для определения скорости необходимо произвести следующие расчеты
Если тело ускоряется в проекции оси ОХ, то скорость можно определить по следующему уравнению
Если α > 0, то движение ускоряется равномерно.

Если тело замедляется в проекции оси ОХ, то скорость рассчитывается следующим образом

Графически зависимость ускорения от времени, т.е. график ускорения при равноускоренном движении тела, можно выразить как
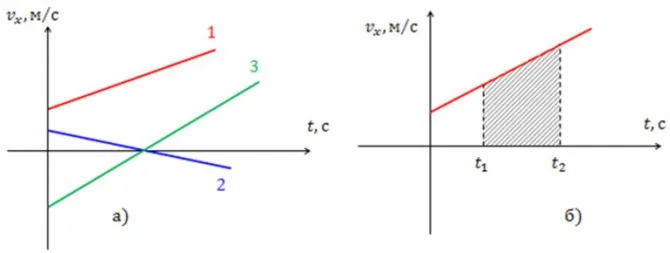
Задачи по кинематике, их решение
Рассмотрим маршрут велосипедиста от одного места до другого. Половина расстояния была пройдена со скоростью 12 км/ч (⌘(v_1 \)). Затем, вторую половину времени движется со скоростью 6 км/ч (ʿ (v_2 \)). На оставшемся расстоянии путешественники шли со скоростью 4 км/ч (⌘ (v_3 \)). Рассчитайте среднюю скорость велосипедиста.
В этом примере рассматривается проблема равномерного линейного движения тела. Процесс можно представить в общих чертах:.

Для каждого участка маршрута необходимо создать уравнения движения.
Кроме того, могут возникнуть дополнительные условия проблемы.
Преобразуйте уравнения и замените числа.
ОТВЕТ: средняя скорость составляет ߰(7 \)км/ч.
Тело было брошено вертикально вверх. Начальная скорость составляла 3,13 м/с (⌘(v_0 \)). К тому времени, когда тело достигло максимальной высоты полета, второй объект с той же начальной скоростью, что и первый, был выброшен из стартовой точки. Необходимо определить, на каком расстоянии от точки литья тела встречаются. Сопротивление воздуха в решении пренебрежимо мало.
В общих чертах движение тел можно представить следующим образом

Для вычисления координат постоянно движущегося тела необходимо уравнение, представляющее движение тела, брошенного вверх. Для первого тела уравнение становится
Для второго тела можно задать следующее уравнение
Следующее уравнение может быть получено из состояния проблемы. Это показывает, что второе тело было брошено позже первого при максимальном подъеме.
Объединение уравнений в трех типах систем относительно величины ⌘ (h \) дает
ОТВЕТ: тела встречаются на высоте \(0.37 \)м.
Камень упал в свободном падении и прошел вторую часть своего пути за 1 секунду. Вычислите высоту, на которой упал камень ⌘(h \).
Ось y системы координат, в которой падает камень, направлена вертикально вниз. Точку падения камня можно считать началом системы координат. Законы движения этого объекта, спроецированного на оси, имеют вид
Время падения камня рассчитывается по следующему уравнению
Следующее уравнение применимо к центру пути, по которому движется камень
Время, необходимое телу для прохождения второй половины заданного пути в рассматриваемом состоянии, ⌘(t_2 \), рассчитывается по следующему уравнению
По этой формуле можно рассчитать высоту.
ОТВЕТ: камень упал с высоты ⌘(57,7 \)м.
Решение задач по кинематике основано на простом уравнении. Успех результата зависит от правильного применения уравнения в конкретном случае. В процессе изучения физики может возникнуть несколько трудностей. Простое решение — обратиться в Phoenix.Help.
Скорость — это натуральная величина, равная расстоянию, пройденному телом в единицах времени. Она обозначается латинской буквой V и измеряется в метрах в секунду (м/с). Время обозначается t, измеряется в секундах, а расстояние — s, измеряется в метрах.
Схемы задач на встречное движение
Для проектирования противоположных движений нарисуйте две острые стрелки, направленные друг на друга. Обозначьте место встречи флажком.
Если проблема противоположной или исходящей циркуляции — это проблема общей скорости. Скоро на моем сайте будет больше уроков о них.
Задача 4. Два пешехода поставили точку, чтобы A и B встретились одновременно. Скорость одного из них составляет 5 км/ч, а другого — 3 км/ч. Если известно, что расстояние между объектами составляет 24 км, сколько времени им потребуется?
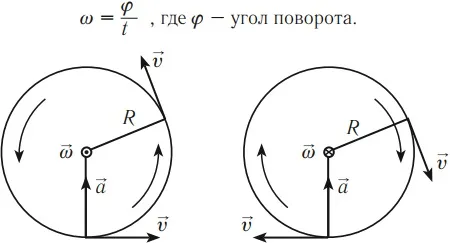
Решение
5 + 3 = 8 км/ч — общая скорость
Задачи на движение в одном направлении
Вопрос 5: Два пешехода одновременно выходят из пунктов A и B в одном направлении. Передний пешеход двигался со скоростью 3 км/ч, а второй — 5 км/ч. Если расстояние между пунктами 2 км, то за какое время второй пешеход догонит первого?
Здесь нам нужно найти скорость сходимости. Поскольку один пешеход шел быстрее другого, расстояние между ними сократилось на 2 км/ч (было рассчитано 5 — 3 = 2 км/ч). Поскольку начальное расстояние между точками равно 2 км, то за время
1 час на встречу с пешеходами.
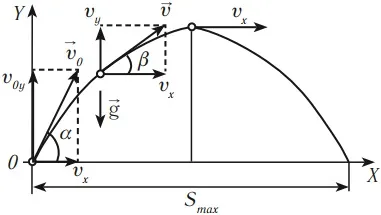
В скобках указаны одна или несколько переменных, от которых зависит натуральный размер. Характерные точки добавляются к символам физических величин для обозначения специфических различий.
Средняя скорость
Как можно сравнить скорости неравномерных движений?
Один из способов сделать это — использовать такие понятия физики, как средняя скорость.
Идея заключается в том, чтобы игнорировать изменения скорости в течение периода и рассматривать только начальный и конечный моменты. Такие измерения полезны, когда необходимо оценить общий результат движения.
Действительно, как правило, целью движения является прибытие в пункт назначения в требуемый момент времени. Как это достигается, часто не имеет значения. Тело сразу же начинает двигаться и равномерно достигает конечного пункта назначения. Как и автомобиль, он может сначала ускоряться, а затем одновременно замедляться до конечного пункта назначения. Наконец, тело может двигаться «рывками», делая некоторые остановки во время движения, но в то же время снова достигая конечного пункта назначения.
Во всех трех упомянутых случаях важно то, что тело начало и закончило движение в одно и то же время и прошло одинаковое расстояние во время движения. То, что произошло во время путешествия, не принимается во внимание.
Скорость, рассчитанная только по моменту первоначального движения, называется средней скоростью. Чтобы найти среднюю скорость, необходимо найти причину полного смещения в точке, где это смещение произошло.
Например, если автомобиль начинает разгон в нулевой момент времени, разгоняется до 50 км/ч, затем замедляется до 40 км/ч и останавливается в 600 м от начальной точки через 1 минуту, найдите 600 м, чтобы найти среднюю скорость движения. 60 s. Средняя скорость составляет 10 м/с.

Рисунок 3.Средняя скорость.
Центробежное ускорение — это характеристика скорости изменения направления линейной скорости. Он называется тузом. Единицей измерения центра ускорения является М/S2. Типы расчетов следующие.
Как найти скорость, время и расстояние — формулы и дополнительные параметры
Скорость, время, расстояние — введите и найдите дополнительные параметры.
Скорость — это натуральная величина, равная расстоянию, пройденному телом в единицах времени. Она обозначается латинской буквой V и измеряется в метрах в секунду (м/с). Время обозначается t, измеряется в секундах, а расстояние — s, измеряется в метрах.
Все три размера относятся к процессу движения и обеспечивают равномерное и равномерное ускорение.
Равномерное движение
Чтобы найти скорость, время и расстояние при равномерном движении, необходимо использовать следующее уравнение
Если скорость объекта изменяется на одну и ту же величину за единицу времени, называемую ускорением (обозначается буквой a, измеряется в м/с 2), то движение называется равномерно ускоряющимся. Если тело действует с одинаковым ускорением, то ускорение отрицательное (тело тормозит). Уравнение используется для расчета необходимых параметров.
- Скорость: v=v0 + at, где v0 – начальная скорость тела на данном участке движения;
- Время: t=(v-v0) / a, где v-v0 – изменение скорости за определенный промежуток времени;
- Расстояние: s=v0*t + a*t 2 /2.
Свободное падение
Тип движения, которое равномерно ускоряется только под действием силы тяжести, называется свободным падением. Его основная характеристика — не зависящее от веса ускорение свободного падения. Этот показатель известен как латинская буква g и равен 9,81 м/с2 на полюсах и 9,78 м/с2 на экваторе (большинство расчетов часто дают среднее значение 9,8 м/с2). Формула цены выглядит следующим образом.
- Скорость: v=v0-gt; (знак «-» появляется из-за принятой системы координат: ось y, вдоль которой движется тело, направлена вверх, тело падает вниз);
- Время: t=(v-v0)/g;
- Расстояние: y=y0+ v0* t-g * t 2/2, где y0 – начальное положение тела над поверхностью земли.








