Вопрос 3: На рисунке показан радиус AB через рассеивающую линзу. Также показано положение фокуса объектива. Спланируйте ход падающего луча.
Проверка домашнего задания
(2) Вопросы перед занятием (см. презентацию).
1.Какая фигура правильно показывает ход радиуса через стеклянную пластинку в воздухе?
2. какая из следующих фигур правильно представляет собой зеркальное изображение уровня вертикального положения?

3. радиус переходит из стекла в воздух, преломляясь на границе раздела двух сред. Какое из направлений 1-4 соответствует преломленному лучу?

4. котенок врезается в плоское зеркало со скоростью v = 0,3 м/с. Само зеркало удаляется от котенка со скоростью u = 0,05 м/с. С какой скоростью котенок приближается к своему изображению в зеркале?
Изучение нового материала
Вообще, слово линза — это латинское слово, которое переводится как чечевица. Чечевица — это растение, плоды которого очень похожи на горох, но горошины не круглые и имеют вид полой лепешки. Поэтому все круглые очки такой формы называли чечевицей.
Первое упоминание о линзах сделано Аристофаном (424 г. до н.э.) в его древнегреческом произведении «Нефера», где огонь добывается с помощью выпуклого стекла и солнечного света. Возраст самой старой из найденных линз составляет более 3 000 лет. Это объектив SO -CALLED NIMRUD. Он был обнаружен Остином Генри Рудьярдом в 1853 году во время раскопок в одной из древних ассирийских столиц Нимруде. Линза грубо овальная, крупная, выпуклая с одной стороны и плоская с другой. Сегодня он находится в Британском музее, главном музее истории и археологии Великобритании.
Линза Нимруда
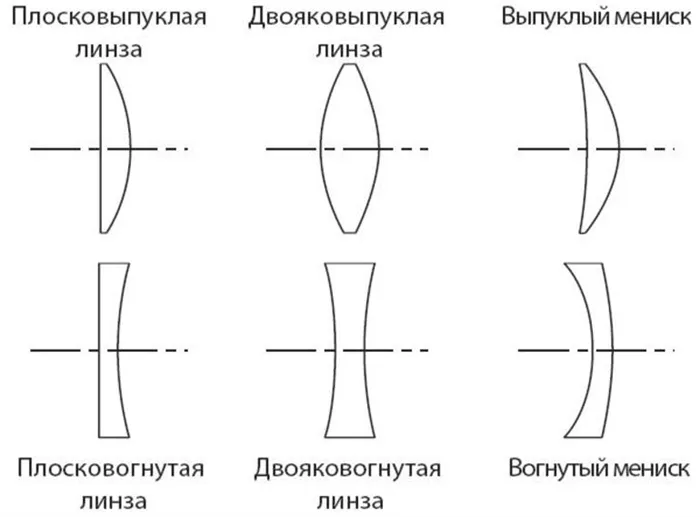
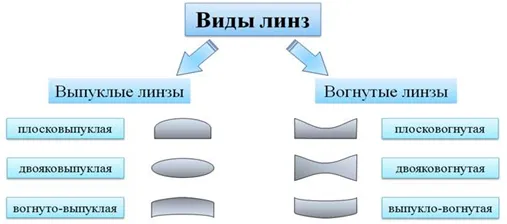
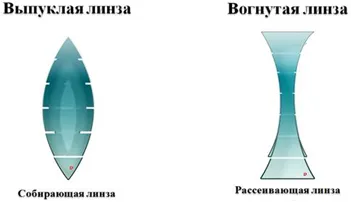
Таким образом, в современном понимании линза — это прозрачное тело, окруженное двумя сферическими поверхностями. (Тетрадь) Наиболее распространенным типом линз является сферическая линза, в которой в качестве ограничивающей поверхности выступает пуля или сфера и один уровень. В зависимости от взаимного расположения сферической или сферической поверхности и уровня различают выпуклые и полые линзы. (Дети рассматривают линзы оптического набора).
Изогнутые линзы делятся на три типа. А именно, плосковыпуклые, двояковыпуклые и полые линзы классифицируются как плосковыпуклые, двояковыпуклые и выпуклые.
Каждую выпуклую линзу можно рассматривать как комбинацию параллельных плоских стеклянных стержней в центре линзы, разрезающих призму, которая расширяется к центру линзы, в то время как каждая полая линза имеет призму, выведенную с центра линзы, расширяющуюся к краю.
Если призма сделана из материала, визуально более плотного, чем ее окружение, она, как известно, отклоняет луч к своему основанию. Таким образом, параллельные пучки света сходятся (называются коллекторами) под действием изогнутых линз, и наоборот. Параллельные пучки света становятся расходящимися (называемыми косыми) с полыми линзами.
Для простоты и удобства рассмотрим линзы, толщина которых пренебрежимо мала по сравнению со сферическими лучами света. Такие линзы называются мелкозернистыми. Отныне, когда бы мы ни говорили о линзах, мы всегда будем иметь в виду тонкие линзы.
Тонкая линза характеризуется следующим образом: если линза является всасывающей, то она изображается в виде линии со стрелкой, указывающей в сторону от центра линзы по краю; если линза является скептической, то стрелка указывает на центр линзы.
Условное обозначение собирающей линзы
Условное обозначение рассеивающей линзы

Зрительный центр линзы — это точка, где нет лучей света.
Каждая линия, пересекающая зрительный центр линзы, называется оптической осью.
Зрительная ось, проходящая через центр сферической поверхности, прилегающей к линзе, называется главной зрительной осью.
Точка, в которой луч света пересекает линзу параллельно ее главной оси (или ее продолжению), называется главным фокусом линзы. Следует помнить, что каждая линза имеет два основных фокуса, один вперед и один назад, потому что каждая линза преломляет свет, падающий в двух направлениях. Обе эти фокусные точки симметричны относительно зрительного центра линзы.
Например, теорема Пифагора полезна при расчете нормального фокусного расстояния для размера матрицы камеры. Необходимо рассчитать длину диагонали датчика. Она равна общему корню квадратному и ширине датчика.
Задачи на тему «Тонкие линзы» с решением

Задачи геометрической оптики не так уж сложны, если потратить некоторое время на их решение. Сегодня в нашей обычной естественной рубрике мы рассмотрим несколько примеров проблем с тонкими линзами.
Хотите быть в курсе текущих академических новостей? Заходите в наш телеграм-канал! А тем, кто хочет получать скидки и бонусы, мы рекомендуем проверить наш второй канал клиентов.
Тонкая линза: задачи
Достаточно знать несколько типов тонких линз для решения задач геометрической оптики. Это правда, что у вас никогда не может быть слишком много типов. Поэтому мы собрали их. Они могут помочь решить проблемы с другими вопросами. Также для тех, кто не знает, как подступиться к решению задач по физике, мы рекомендуем прочитать общий меморандум для их решения.
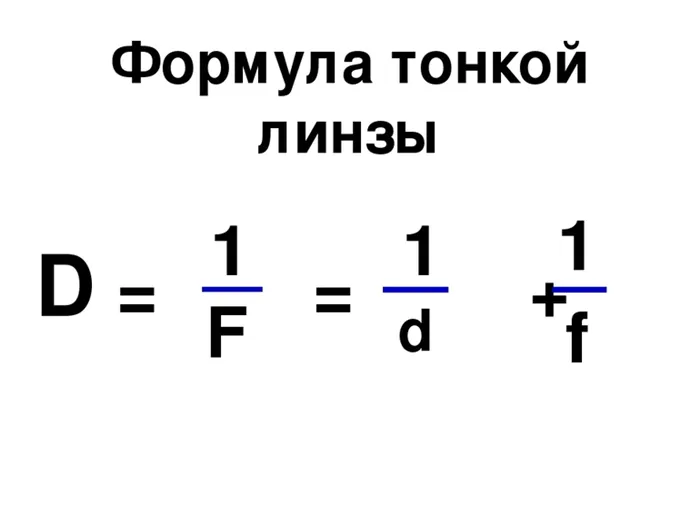
Задача №1. Формула тонкой линзы
2.5 Объектив визуальной силы ДПТР размещается на расстоянии 0,5 м от сильно освещенного объекта. На каком расстоянии должен располагаться экран, чтобы можно было визуализировать объект?
Объектив является коллекционным (его визуальная способность положительная). Запишите тип тонкой линзы:.
Замените значение из условия, так как f = 1 d. Напишите.
2, 5 = 1 0, 5 + 1 + f f = 2 m
Задача №2. Формула тонкой линзы
Яркое пятно находится на уровне через двойной камин тонкой линзы, заданной главной визуальной осью. Определите, какая из четырех точек на рисунке соответствует соответствующему изображению светового пятна.
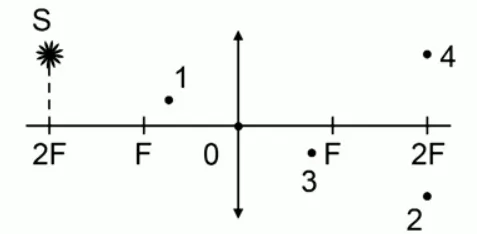
Как показано на рисунке, концентрическая линза нарисована в зрительном центре точки 0. Яркая точка S равна двум фокусным точкам линзы.
Сконструируем картинку: один радиус проходит через оптический центр линзы, а после преломления через камин проходит второй луч, параллельный главной зрительной оси. Точка пересечения на расстоянии двойного фокуса является изображением S.
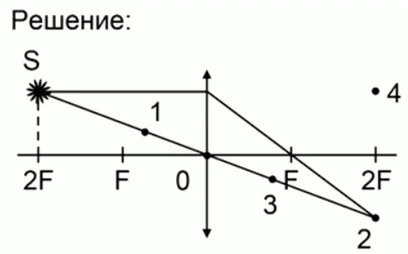
ОТВЕТ: изображение S соответствует точке 2.
Это решение возникает геометрически, но им можно управлять, используя тип линзы. Замените D на 2F, чтобы получить тот же результат.
Задача №3. Формула тонкой линзы
Объект размером 3 см находится на расстоянии 40 см от тонкой собирающей линзы. Зрительная сила объектива определяет высоту изображения для 4-х биноклей.
Пусть человек напишет о тонкой коллекционной линзе и типе увеличения линзы.
1 f = 1 d + 1 f- h = h h = f d
Перепишем эти соотношения в представлении f = 1 d
Замена цены типа h — это остаток от расчета.
h = h d d -d -1 = 0, 03-0, 4 4-0, 4-1 = 0, 05 м
Ответ: 0,05 м.
Задача №4. Формула тонкой линзы
Высота объекта составляет 2 см. Каково фокусное расстояние линзы на расстоянии f = 4 м от экрана? Какова высота изображения объекта на экране при H = 1 м?
Найдите фокусное расстояние типа объектива.
1 f = 1 d + 1 f f = f d d + f
Напишите уравнение для увеличения линзы и выразите d.
Запишите свой окончательный ответ: d
Ответ: 0,08 метра.
Задача №5. Формула тонкой линзы
Создайте изображение отрезка AB перед стремящейся линзой так, чтобы расстояние от предмета до линзы было d = 2 F. Что это за картина?
Создайте изображение в соответствии с правилами геометрической оптики.
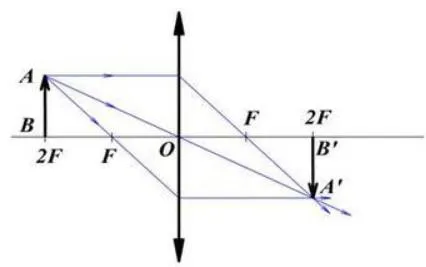
Ответ: см. выше.
Вопросы на тему «Тонкая линза»
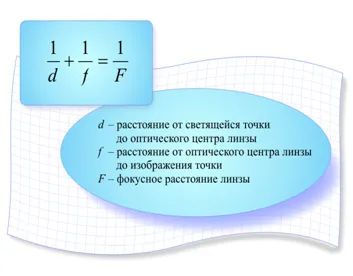
Вопрос 1. какое уравнение называется типом тонкой линзы?
Ответ. Типы тонких линз следующие.
- F – фокусное расстояние;
- d – расстояние от линзы до предмета;
- f – расстояние от линзы до изображения.
ВОПРОС 2. В чем разница между коллекторными и рассеивающими линзами?
Ответ. Для собирающих линз f считается положительным; для рассеивающих линз f считается отрицательным. Поэтому аспирирующая линза создает реальное изображение, а рассеивающая линза — иллюзорное.
Вопрос 3: Каково фокусное расстояние объектива?
Ответ. Фокусное расстояние объектива — это расстояние между оптическим центром объектива и его главным фокусом.
Вопрос 4Какова преломляющая сила линзы?
Ответ. Оптическая сила является обратной величиной фокусного расстояния. Он характеризует преломляющую силу линзы.
Вопрос 5: Может ли преломляющая сила линзы быть отрицательной?
Ответ. Да. Для рассеивающих линз светосила получается со знаком минус.
Проблемы с решением проблем или других задач? Обратитесь в нашу профессиональную службу поддержки студентов!
Иван Колобков, также известный как Джони. Он является торговцем, аналитиком и копирайтером в компании Zaochnik. Многообещающий молодой писатель. Он любит физику, необычное и творчество К. Буковски.
Здесь b — расстояние линзы от изображения. a — расстояние линзы от предмета. f — фокусное расстояние линзы. b — расстояние линзы от изображения. f — фокусное расстояние линзы от предмета. Расстояние в уравнении (1) можно определить по простому правилу. Если расстояние измеряется в обратную сторону от линзы, добавляется символ ‘+’, в противном случае добавляется ‘-‘.
Какое фокусное расстояние выбрать
Формула для нормального фокусного расстояния проста. Она соответствует длине диагонали стола. Для так называемых полнокадровых сенсоров это 24×36 мм. Длина диагонали и нормальное фокусное расстояние составляют 43 мм соответственно. Однако на практике фокусное расстояние 50 мм является упрощением.
Фактическое фокусное расстояние также зависит от размера матрицы камеры. Существует множество камер с меньшими матрицами. Это означает, что нормальное фокусное расстояние изменяется из-за меньшей длины диагонали.
Фокусное расстояние объектива всегда указывается для камер с полнокадровой матрицей, также известной как «полный кадр». Если формат матрицы камеры отличается, например, Micro Four Thirds, DX или APS-C, фокусировка должна быть пересчитана с использованием так называемого «кроп-фактора».
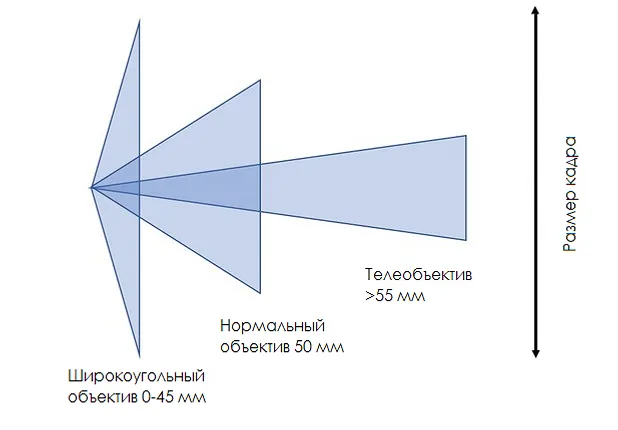
Съемка изображения с меньшим фокусным расстоянием, чем обычно, приведет к тому, что изображение будет больше, чем может воспринять глаз. Напротив, при больших фокусных расстояниях фрагменты изображения кажутся меньше, чем изображение, видимое глазом. Поэтому рекомендуется использовать объективы с меньшим фокусным расстоянием для пейзажной и архитектурной съемки и с большим фокусным расстоянием для съемки дикой природы.
Формула для расчета фокусного расстояния
В зависимости от интересующего соотношения можно выполнить различные расчеты фокусного расстояния. Можно использовать упрощенные формулы, которые также могут дать очень точные результаты.
Например, теорема Пифагора полезна при расчете нормального фокусного расстояния для размера матрицы камеры. Необходимо рассчитать длину диагонали датчика. Она равна общему корню квадратному и ширине датчика.
Если вы хотите узнать, какой объектив для полнокадровой камеры подходит для вашего оборудования, сначала нужно рассчитать коэффициент отсечения камеры. Затем просто умножьте фокусное расстояние объектива на значение кроп-фактора. Например, коэффициент отсечения для камеры Micro Four Thirds составляет 2. Поэтому фокусное расстояние 25 мм камеры Micro Four Thirds равно фокусному расстоянию 50 мм полнокадровой камеры.
Оптическая линза — это объект, изготовленный из прозрачного материала (например, стекла, прозрачного хрусталя или пластика), окруженный двумя сферическими поверхностями с вершинами на одной оси, называемой оптической осью (рис. 1).
Основная формула
Существует идентифицируемое представление характеристик оптического стекла. Он называется базовым типом объектива. Его также называют уравнением линзмастера. Это уравнение создает четкую зависимость между изображением расстояний до объекта s и s’, коэффициентом преломления материала линзы и окружающей среды, а также радиусами кривизны R1 и R2. Мы можем сказать об этом так:.
где величины s, s’, R1 и R2 измеряются в метрах (м) в системе СИ. Расстояние от зрительного центра до объекта (s) и его изображения (s’) может быть как положительным, так и отрицательным. Символы определяются следующим образом. Если объект находится перед объективом, т.е. в левой части изображения, он воспринимается знаком +. Если он находится в правой части изображения, то его место занимает знак +.

Основное уравнение можно найти самостоятельно, изучив преломление одного луча через каждую поверхность. Это уравнение применимо ко всем типам рассматриваемых объектов.
Понятие о фокусе
При изучении тонкого оптического стекла особое внимание уделяется изображению фокусных расстояний объекта f и f’. Эти величины определяются следующим образом
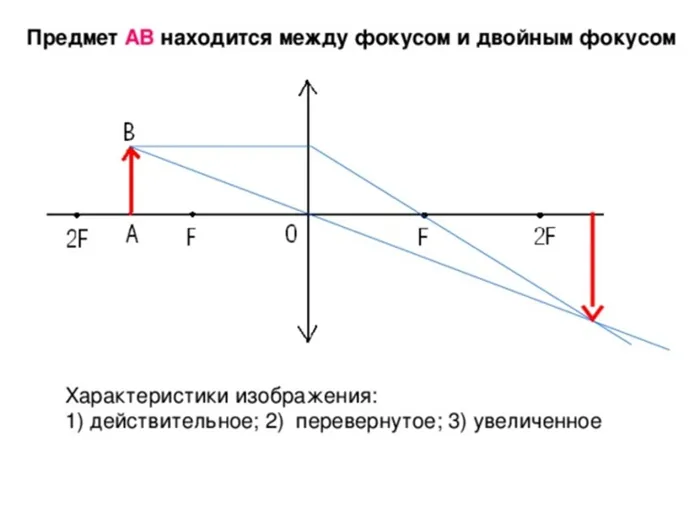
- Фокус предмета — это точка F, в которую нужно поместить сам предмет, чтобы любой выходящий из него луч, пройдя через линзу, выходил параллельным ее основной оптической оси. Эта ось проходит через центр линзы перпендикулярно обеим ее поверхностям. Соответственно фокусное расстояние f определяется как дистанция от предмета до оптического центра O, то есть длина FO. Математически это означает, что изображение предмета будет находиться в бесконечности, и f=s.
- Фокус изображения — это точка F’, в которую собираются все лучи, падающие на линзу из бесконечности, то есть параллельно основной оптической оси. В таком случае получается, что сам предмет находится в бесконечности, и f’=s’.
Учитывая определение фокусного расстояния объекта и его изображения, следующее соотношение между f и f’ может быть записано с помощью основного уравнения
Полученное уравнение можно использовать для выведения гауссовой формы типа тонкой линзы. Следующая форма.
Это выражение применимо ко всем средам, а не только к воздуху. Его также называют типом объектива с фокусным расстоянием.
Гауссова форма
Его использование позволяет сделать некоторые важные выводы. Полезно переписать его в следующем формате.
При создании изображения объект съемки обычно располагается слева от объектива. Это означает, что сумма 1 / s всегда будет меньше нуля (1 / s0). Для положительного оптического стекла возможно формирование как действительных (1 / s’> 0), так и мнимых (1 / s’) чисел.<0) изображения, все зависит от величины слагаемых противоположного знака.
В случае полых линз фокусное расстояние f’ отрицательно, поэтому оба члена в правой части гауссовой формы имеют отрицательный знак и не требуют изменения. Этот факт показывает, что какой бы предмет ни был помещен перед светорассеивающим стеклом, его изображение всегда будет превосходным.
Для простоты и удобства рассмотрим линзы, толщина которых пренебрежимо мала по сравнению со сферическими лучами света. Такие линзы называются мелкозернистыми. Отныне, когда бы мы ни говорили о линзах, мы всегда будем иметь в виду тонкие линзы.
Эксцентриситет эллипса
Эксцентриситет эллипса — это отношение фокусного расстояния к главной оси и выражается как
Эксцентричность характеризует степень «выравнивания» дефицита. если это круг. в этом случае дефицит преобразуется в дробь. В некоторых случаях. Для фокального радиуса мы приводим такое выражение без доказательства: .
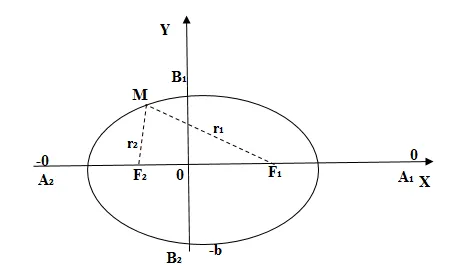
Недостаток может быть создан механически. Найдите полуось из уравнения нормали, а затем вычислите расстояние между полуосями.
Постройте лежаки печи на расстоянии друг от друга. Прикрепите нерастянутый конец нити к точке и к. Натяните нить кончиком карандаша и проведите им по плоской поверхности так, чтобы нить скользила по острию. Карандашом очерчивается полуось. Потяните нить в противоположном направлении и нарисуйте вторую половину эллипса.
Примеры решения задач
Эллипс задается уравнением и точкой. Он должен:.
- убедиться, что точки и лежат на эллипсе;
- найти полуоси эллипса и координаты его фокусов;
- найти расстояние от точки к фокусам;
- убедиться, что сумма этих расстояний равна длине большой оси;
- найти эксентриситет эллипса.
1. замените координаты точки в левой части эллиптического уравнения.
-нет смысла. Аналогично:.
2. из регулярного приведенного эллиптического уравнения следует. Из равенства следует.
-половина фокусного расстояния. Координаты фокусной точки и.
3.Найдите фокальный радиус точки.
4. найдите сумму, удовлетворяющую определению дефицита.
5. найдите эксцентриситет, используя уравнение 5.
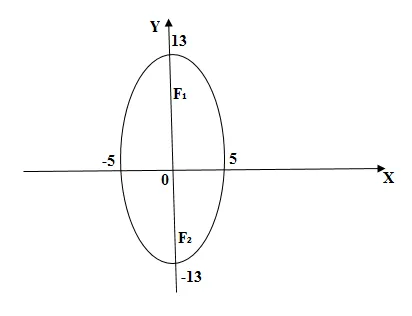
Найдите ось, пик и фокус дефицита.
Сведите нормальное уравнение к нормальному уравнению.
,. Пик эллипса на сайте 、、、、、、. Создайте вершины на координатных осях и соедините их сплошными линиями (см. рис. 2). В этом случае промежуток, вытянутый вдоль оси, больше, поэтому можно найти полуфокальное расстояние.
Фокус на и. (см. рис. 3).
Определите ось, пик и фокус отсутствия или Сконструируйте недостаток.
Сравнивая последнее уравнение с уравнением (2), получаем
,. Отсюда, оси эллипса:, и координаты вершины: 、、、、、、、、、. Далее от уравнения:.
. Таким образом, в фокусе дефицита находится точка: и. Чтобы создать эллипс, отложите оси и вершины соответственно и соедините их плавной линией (см. задачу 1).
Наблюдение! Если полуось находится в обычном уравнении, то фокус эллипса является осью и тогда
Эллипс — фокусное расстояние формы, уравнение, свойства и эксцентриситет Обновлено: 16 апреля 2020 г. Предоставлено: Научные статьи.Ru








