Благодаря научным достижениям и быстрому развитию технологий современные люди имеют доступ к быстрым средствам передвижения. Чтобы обогнуть весь мир на самолете, требуется не более суток. Быстрая скорость неизбежно связана с понятием перегрузки.
Ускорение свободного падения
Гравитационное ускорение — это ускорение тела под действием силы тяжести, если на это тело не действуют другие силы или если их действие не отменяет друг друга.
Ускорение силы тяжести обозначается $ g $. Дальность земной поверхности составляет 9,78 \ \ frac $ 9,832 \ frac $. Ускорение силы тяжести выше на полюсах и ниже на экваторе. Среднее (типичное или нормальное) значение ускорения силы тяжести на Земле считается равным $ g = 9,80665 \ frac $. В задаче значение ускорения силы тяжести принимается равным $ g = 9,81 \ frac $. В качестве альтернативы, часто принимают $ g = 10 \ frac $, если расчеты приблизительны.
Согласно общему закону Галилея, все тела в одном и том же гравитационном поле падают с одинаковым ускорением. Это означает, что в определенной точке Земли ускорение силы тяжести одинаково для всех тел. Изменение величины гравитационного ускорения у поверхности Земли в зависимости от широты обусловлено суточным вращением планеты вокруг своей оси и тем, что форма Земли отличается от формы шара (Земли). (сплющенный).
Зависимость ускорения свободного падения от высоты над уровнем Земли
Если пренебречь суточным вращением Земли, то сила тяжести ($ p = mg $) равна по величине силе тяжести (f).
где $ m $ — масса Земли- $ r $ — расстояние от центра Земли до рассматриваемого тела- $ \ гамма $ — гравитационная постоянная. Тип (1) применяется, когда тело находится вблизи поверхности Земли и гравитационное ускорение равно.
Ускорение, рассчитанное по типу (2), называется ускорением силы тяжести на уровне моря.
Предположим, что тело находится на высоте $ h $ над землей и что сила тяжести на тело равна.
Здесь $ r_z $ — радиус Земли. В этом случае ускорение свободного падения зависит от высоты, на которой находится тело.
Изменения в ускорении свободного падения на высоту, значительно меньшую, чем радиус Земли, обычно игнорируются. Ускорение силы тяжести считается постоянным.
Влияние вращения Земли на ускорение свободного падения
Как уже упоминалось, на ускорение свободного падения влияет вращение планеты вокруг своей оси. Предположим, что тело массой $ m находится на широте $ \ varphi $. Вместе с планетой тело движется, и его орбита проходит следующий цикл радиуса $ r $.
Где $ r_z $ — радиус Земли. Центробежное ускорение нашего тела в этом случае ($ a_n $) имеет цену
где $ t $ — период оборота земли. Гравитация ($ f $) может быть проанализирована на две составляющие: центробежная сила ($ f_n $) и сила тяжести ($ p $). Везде, кроме полюсов, сила тяжести меньше силы центробежной силы. Везде, кроме Эквадора и полюсов, гравитация не направлена точно на центр Земли, а немного удалена от него.
Из-за вращения Земли сила тяжести на полюсах больше, чем на экваторе — наша планета сплющена.
Ускорение свободного падения столба ($ g_p $) максимально. Центростремительное ускорение равно нулю, поэтому радиус полюса ($ r_p $) минимален.
Ускорение свободного падения в Эквадоре ($ g_e $) — это разница.
Где $ r_e $ — экваториальный радиус Земли. $ \ frac $.<\gamma M>Это называется напряженностью гравитационного поля Земли.
Благодаря научным достижениям и быстрому развитию технологий современные люди имеют доступ к быстрым средствам передвижения. Чтобы обогнуть весь мир на самолете, требуется не более суток. Быстрая скорость неизбежно связана с понятием перегрузки.
Ускорение свободного падения
Ускорение силы тяжести — это ускорение объекта под действием силы тяжести. Она выражается буквой g и измеряется в м/с². На поверхности Земли ускорение силы тяжести составляет приблизительно 9,81 м/с².
На полюсах (южном и северном) ускорение силы тяжести больше, а на экваторе — меньше. Это объясняется двумя фактами:.
- Земля — не идеальный круг, а приплюснутый шар и её радиус на полюсах меньше, чем на экваторе (ускорение зависит от радиуса),
- центробежные силы (при вращении Земли) минимально компенсируют гравитацию больше на экваторе, чем на полюсах.
В вакууме ускорение свободного падения не зависит от массы, поэтому объекты падают с одинаковой скоростью.
Таблица для ускорения свободного падения небесных объектов
| Небесное тело | g (в м/с²) |
|---|---|
| Луна | 1,62 |
| Солнце | 274 |
| Меркурий | 3,72 |
| Венера | 8,87 |
| Земля | 9,81 |
| Марс | 3,711 |
| Юпитер | 24,79 |
| Сатурн | 10,44 |
| Уран | 8,87 |
| Нептун | 11,15 |
Как найти ускорение свободного падения?
Формула ускорения свободного падения
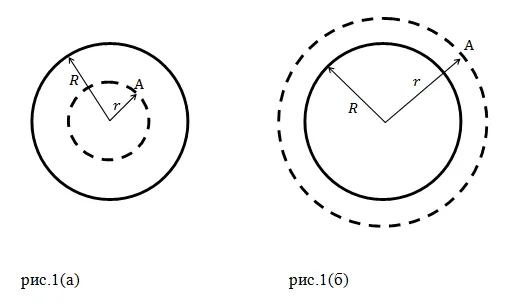
Где g — гравитационное ускорение G — гравитационная постоянная M — масса планеты R — радиус планеты
Гравитационная постоянная («G», не путать с «g») — это фундаментальная физическая постоянная, которая приблизительно равна.

Гравитационная сила между двумя объектами (G) связана с их массами (m1 и m2) и расстоянием между ними (R) следующим уравнением.

Пример расчёта ускорения свободного падения (для Земли):

g — гравитационное ускорение G — гравитационная постоянная m — масса планеты R — радиус планеты
Ускорение силы тяжести — это ускорение объекта под действием силы тяжести. Она выражается буквой g и измеряется в м/с². На поверхности Земли ускорение силы тяжести составляет приблизительно 9,81 м/с².
Движение тела, брошенного вертикально вверх
Аналогично можно рассмотреть движение объекта, который вырывается вертикально вверх с определенной начальной скоростью. Например, мяч подбрасывают вверх.
Ось координат должна быть направлена прямо над точкой, в которую бросается тело. В этот раз тело движется так же медленно и теряет скорость. В высшей точке тело имеет нулевую скорость. Применяя тип кинематики, мы можем написать:.
Подставьте v = 0, чтобы найти время, за которое тело поднимется на максимальную высоту.
Время падения равно времени подъема, и тело возвращается на землю в момент t = 2 v0g.
Максимальная высота подъема тела, брошенного вертикально:.
См. схему ниже. На нем изображен график скорости объекта для трех случаев движения с ускорением a = -g. Рассмотрим каждый из них, заранее уточнив, что в данном примере все значения округлены, а ускорение силы тяжести принято равным 10 м с 2 .
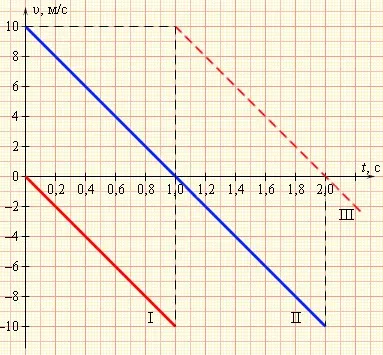
Первый график показывает падение объекта с высоты без начальной скорости. Время падения tn = 1 с. Из уравнения и графика легко понять, что высота, с которой упало тело, равна h = 5 м.
Второй график показывает движение объекта, брошенного вертикально вверх с начальной скоростью v 0 = 10 мс. Максимальная высота подъема h = 5 м. Время подъема и опускания tn = 1 с.
Третий график является продолжением первого графика. Падающий объект отскакивает от поверхности, и его скорость быстро меняется. Дальнейшие движения тела показаны на втором графике.
Движение тела, брошенного под углом к горизонту
С проблемой свободного падения тела тесно связана проблема движения тела, брошенного под определенным углом к горизонту. Поэтому движение по параболической траектории может быть выражено как сумма двух независимых движений вокруг вертикальной и горизонтальной осей.
Вдоль оси OY объект движется равномерно с ускорением g, и начальная скорость этого движения равна v0y. Движение вдоль оси O X равномерное и прямолинейное, а начальная скорость равна v0x.

Условиями для движения вдоль оси OX являются.
x 0 = 0; v 0 x =v0cosα; αx=0.
Условие движения вдоль вала O Y:.
y 0 = 0; v 0 y = v 0 sin a; a y = -g.
Приведите тип движения тела, брошенного под углом к горизонту.
Максимальная дальность достигается при угле A = 45°.
Учитывая максимальную высоту подъема.
Следует отметить, что в реальных условиях движение тела, брошенного наклонно к горизонту, может идти по траектории, отличной от параболы, из-за сопротивления воздуха и ветра. Специальная наука — баллистика — изучает движение тел, запущенных в космос.
Древнегреческие ученые делили все движения на два типа: естественные и вынужденные. Движения тела под действием гравитации считались естественными, поскольку они не имели очевидной причины и были сами по себе.
Сила тяготения
В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Она заключается в следующем. Все тела притягиваются друг к другу с силой, прямо пропорциональной массе тела и обратно пропорциональной квадрату расстояния между ними.
Согласно этому закону, видами гравитационной силы являются
Глобальный закон всемирного тяготения
F — гравитационная сила n
M — масса первого тела (часто планеты) кг
M — масса второго тела кг
R — расстояние b между двумя b.
G — гравитационная постоянная
g = 6,67-10 -11 м 3 -кг -1 -с -2
Когда мы встаем на весы, стрелки отклоняются. Это происходит потому, что масса Земли настолько велика, что гравитация буквально выталкивает нас на поверхность. При яркой луне человек весит в шесть раз меньше.
Закон всемирного тяготения используется для расчета сил взаимодействия между телами любой формы, если размеры тел намного меньше расстояния между ними.
Если взяты две пули, этот закон может быть использован независимо от расстояния между ними. Расстояние r между телами в этом случае равно расстоянию между центрами сфер.
Ускорение свободного падения
Для того чтобы придумать ускорение силы тяжести математическим и красивым способом, необходимо сначала ввести понятие гравитации.
Гравитация — это сила, с помощью которой Земля притягивает все тела.
Гравитационная сила
F — гравитационная сила n
M — масса тела кг
G — ускорение силы тяжести M/S 2
На планете Земля g = 9,8 м/с 2, о чем более подробно будет рассказано позже. 😉
На первый взгляд, гравитация очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли гравитация и вес одинаковы. Вес тела в состоянии покоя численно равен его весу, умноженному на ускорение силы тяжести, разница лишь в точке приложения силы.
Гравитация — это сила, действующая на тело со стороны земли, а вес — это сила, действующая на тело при поддержке или подвешивании. Это означает, что они имеют разные точки приложения: вес в центре масс тела и вес в опоре.
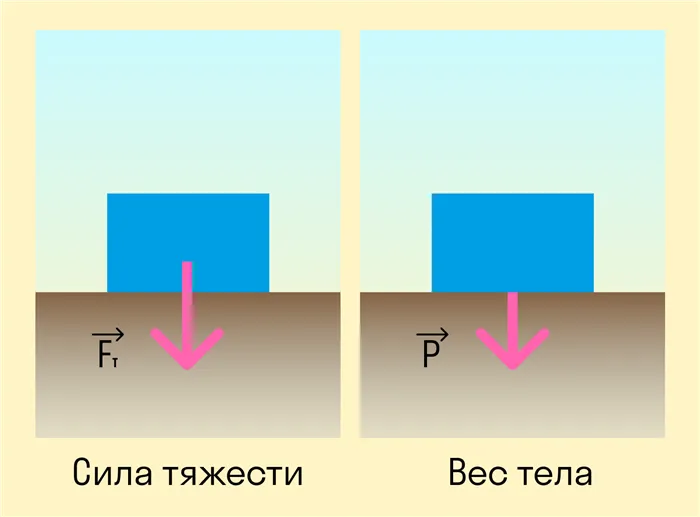
Также важно понимать, что гравитация зависит только от массы и планеты, на которой находится тело. Вес также зависит от ускорения, с которым движется тело или опора.
Например, в лифте вес зависит от того, куда едет пассажир и с каким ускорением. Сила тяжести не зависит от того, куда она движется — она не зависит от внешних факторов.
На первый взгляд, сила гравитации очень похожа на силу притяжения. В обоих случаях мы имеем дело с гравитацией, и это одно и то же. Минута.
Мы можем сказать, что это одно и то же, если имеем дело с объектами, которые притягиваются к Земле и этой планете. Затем мы можем приравнять эти силы и выразить тип для ускорения свободного падения.
Мы приравниваем правую сторону:.
Разделите левую и правую части на массу тела.
Это становится формулой для ускорения свободного падения. Каждая планета имеет уникальное ускорение свободного падения.
Формула для ускорения свободного падения
G — ускорение силы тяжести M/S 2
M — масса планеты в кг
R — расстояние b между двумя b.
G — гравитационная постоянная
g = 6,67-10 -11 м 3 -кг -1 -с -2
Ускорение силы тяжести описывает, насколько быстро увеличивается скорость тела во время свободного падения.
Свободное падение — это ускоренное движение объекта в безвоздушной среде, где на объект действует только сила тяжести.
Ускорение свободного падения на разных планетах
Формулы для ускорения свободного падения уже разработаны. Вычислим ускорение свободного падения планеты Земля.
Для этого вам понадобятся следующие значения.
- Гравитационная постоянная G = 6,67 · 10 −11 м 3 · кг −1 · с −2
- Масса Земли M = 5,97 × 10 24 кг
- Радиус Земли R = 6371 км
Подставим эти значения в формулу:.

Есть некоторые трудности. Значения ускорения силы тяжести Земли имеют много знаков после запятой. В школе мы обычно даем то же значение, что и выше: g = 9,81 м/с2. В тестах ЕГЭ и ОГЭ мы даем g = 10 м /с2 в качестве справочных данных.
И кому же верить?
Это просто. Кем бы ни была проблема, он несет за нее ответственность. На экзаменах g = 10 м/с2, а в школе при решении задачи (если в задаче больше ничего не написано), g = 9,8 м/с2 .
Ниже приведена таблица гравитационного ускорения и других свойств планет, квазипланет и Солнца в нашей Солнечной системе.
Вектор свободного падения всегда направлен вниз. Это можно наглядно увидеть, бросая предметы. Из-за эффекта ускорения его движение постепенно замедляется. Затем он полностью останавливается и направляется в противоположную сторону.
Определение скорости свободного падения
Свободное падение объекта — это равновесное движение под действием силы тяжести. В этот момент другие силы, которые могут воздействовать на тело, либо отсутствуют, либо очень малы, поэтому их влияние не учитывается. Например, когда десантник прыгает с самолета, он свободен в первые несколько секунд после прыжка. Этот короткий период характеризуется ощущением невесомости, подобным тому, которое испытывают астронавты в космических кораблях.
Ученые изучают свободное падение со времен Средневековья. Альберт и Николай Орем из Саксонии изучали это явление, но некоторые их выводы оказались ошибочными. Например, они утверждали, что скорость падения тяжелого предмета увеличивается прямо пропорционально пройденному расстоянию. В 1545 году испанский ученый Д. Сото исправил эту ошибку, установив, что скорость падающего объекта увеличивается пропорционально времени, прошедшему от начала падения объекта.

В 1590 году итальянский физик Галилео Галилей принял закон, определяющий четкую зависимость между расстоянием и временем, пройденным падающим объектом. Он также доказал, что в отсутствие сопротивления воздуха все предметы на Земле падают с одинаковым ускорением, хотя до его открытия считалось, что более тяжелые предметы падают быстрее.
Были обнаружены новые величины, гравитационные и центробежные ускорения. Этот показатель выражается в виде g и составляет от 9,78 м/с2 (на экваторе) до 9,83 м/с2 (на полюсах) и действует в разных точках Земли. Долгота, широта, время и некоторые другие факторы влияют на точность геометрии.
Стандартное значение g считается равным 9,80665 м/с2. Для физических расчетов, не требующих высокой точности, значение ускорения принимается равным 9,81 м /с2. Для простоты расчетов g можно считать равным 10 м /с2.
Чтобы показать, как падает объект в соответствии с выводами Галилея, ученые проводят следующий эксперимент. Предмет разного веса помещается в длинную стеклянную трубку, и через трубку всасывается воздух. Когда трубка перевернута вверх дном, под действием силы тяжести все предметы, независимо от их веса, падают на дно трубки одновременно.
Когда эти же предметы помещаются в среду, они будут падать в разное время в зависимости от их массы, формы и плотности, поскольку гравитация оказывает на них сопротивление.
Формулы для расчетов
Существуют формулы, которые можно использовать для расчета различных величин, связанных со свободным падением. Они используют следующие контракты:.
- u — конечная скорость, с которой перемещается исследуемое тело, м/с;
- h — высота, с которой перемещается исследуемое тело, м;
- t — время перемещения исследуемого тела, с;
- g — ускорение (постоянная величина, равная 9,8 м/с 2 ).
Формула для определения расстояния, пройденного объектом, падающим с известной конечной скоростью и временем падения: h = ut/2.
Уравнение для расчета расстояния, пройденного объектом, падающим с постоянной величиной g и временем: h = gt2/2.
Уравнение для определения скорости падающего объекта в конце падения с известным временем падения: u = gt.
Формула для расчета скорости объекта в конце падения, если известна высота, на которой он падает: u =√2gh.

Интересные факты
Если не вдаваться в науку, то повседневное определение свободного движения — это движение объекта в атмосфере Земли, на которое не влияют другие факторы, кроме сопротивления окружающего воздуха и гравитации.
Время от времени добровольцы соревнуются друг с другом в попытках установить личные рекорды. В 1962 году советский парашютист-испытатель Евгений Андреев установил рекорд, занесенный в Книгу рекордов Гиннесса. Во время прыжка с парашютом он преодолел расстояние в 24 500 метров, не используя парашют в качестве тормоза.
В 1960 году Д. Киттингер из США совершил прыжок с парашютом с высоты 31 000 метров, используя тормозное устройство парашюта.
В 2005 году был установлен рекорд скорости свободного падения — 553 км/ч, а через семь лет был установлен новый рекорд — эта скорость возросла до 1342 км/ч. Этот рекорд принадлежит австрийскому парашютисту Феликсу Баумгартнеру, который известен во всем мире своими опасными трюками.








