В более сложном случае, когда угол между скоростью частицы и напряженностью магнитного поля произвольный, частица движется по спиральной траектории — поступательно за счет компонента скорости, направленного параллельно полю, и по окружности под действием перпендикулярного компонента.
Сила Лоренца
Сила Лоренца — это сила, оказываемая электромагнитным полем на движущийся электрический заряд. Он назван в честь физика, который впервые описал это явление. Название сила Лоренца часто используется в формуле, в которой имеется в виду только магнитная сила:
\\mathrm=\mathrm(E+v B)\
Здесь магнитная сила обозначается через B, заряд частицы через q, напряженность электрического поля через E, а скорость движущейся частицы через v.
Амперная сила, действующая на отрезок проводника длиной Δl с определенной силой тока l в магнитном поле B, F = I ⋅ B ⋅ Δ l ⋅ sin α, может быть выражена в терминах сил, действующих на определенные носители заряда.
Мы обозначаем заряд конкретного носителя заряда через q. В этом случае n представляет собой значение концентрации свободных носителей заряда в проводнике.
Таким образом, выражение n ⋅ q ⋅ u ⋅ S, где S обозначает площадь поперечного сечения предложенного проводника, а u — мера скорости движения расположенных носителей заряда в представленном проводнике, соответствует току, протекающему в проводнике: I = q ⋅ n ⋅ n ⋅ u ⋅ S
Формула для силы в амперах выглядит следующим образом:
\\mathrm=\mathrm \cdot \mathrm \cdot \mathrm \cdot \Delta \mathrm \cdot \mathrm \cdot \mathrm \cdot \sin \alpha\
Полагая, что переменная N, обозначающая число свободных носителей заряда, движущихся в проводнике с площадью поперечного сечения S и длиной Δl, равна произведению n ⋅ S ⋅ Δ l, можно сказать, что сила, действующая на каждую из заряженных частиц, равна выражению
\F_\ = q ⋅ u ⋅ B ⋅ sin α.
Сила, которую мы нашли, называется силой Лоренца. Формула показывает, что величина угла α соответствует углу, образованному вектором магнитной индукции \\\\vec\ и скоростью \\\\.
В принципе, сила Лоренца очень похожа на силу Ампера. Разница в том, что последнее относится ко всему проводнику, который является электрически нейтральным, а первое описывает, как электромагнитное поле действует на одну движущуюся заряженную частицу.
Направление силы Лоренца
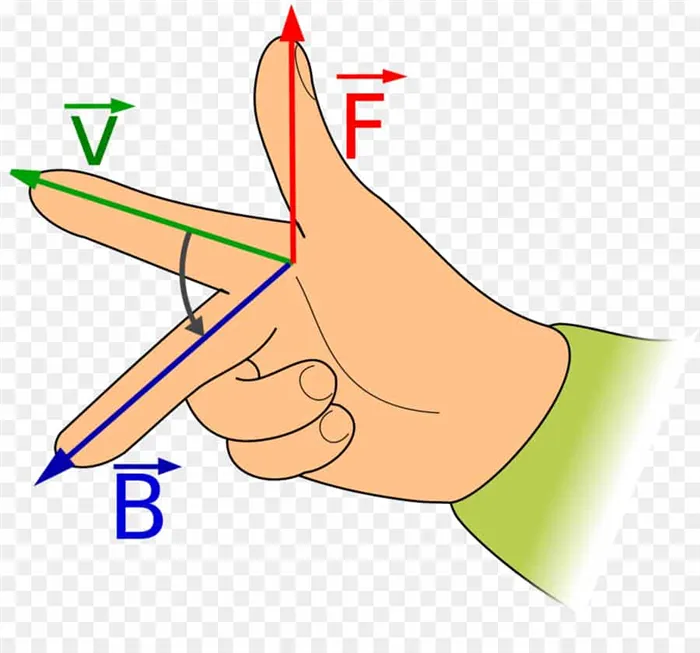
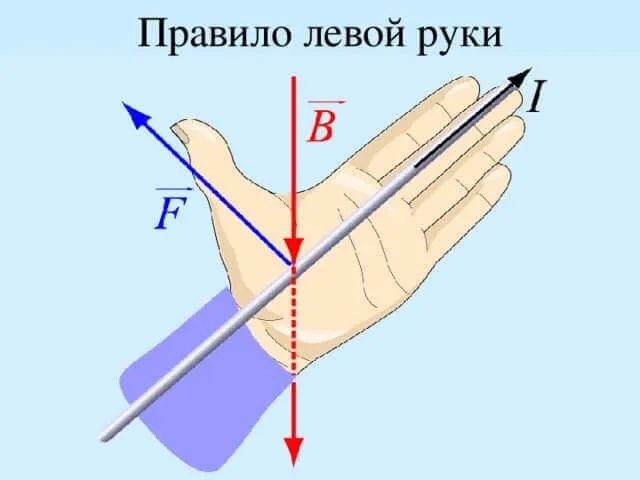
Чтобы определить направление силы Лоренца, мы предполагаем, что она всегда перпендикулярна вектору магнитной индукции. Это означает, что \\\vec\ соответствует направлению в пространстве, вдоль которого магнитные силы не распространяются. Вектор силы Лоренца имеет направление, перпендикулярное вектору \\\vec\. Для определения конечного направления силы можно использовать правило левой руки.
Ладонь должна быть расположена так, чтобы четыре пальца были вытянуты в направлении нагрузки, а положение вытянутого большого пальца совпадало с вектором поля магнитной индукции. Большой палец указывает направление силы Лоренца, действующей на положительный груз.
Если заряд отрицательный, направление силы меняется на противоположное.
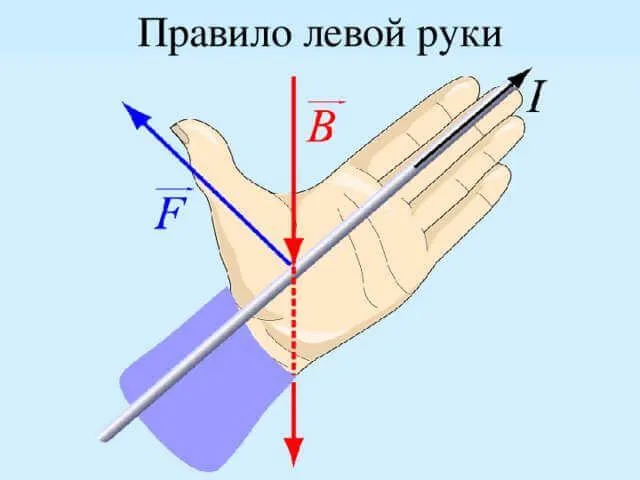
Рисунок 1: Правило левой руки
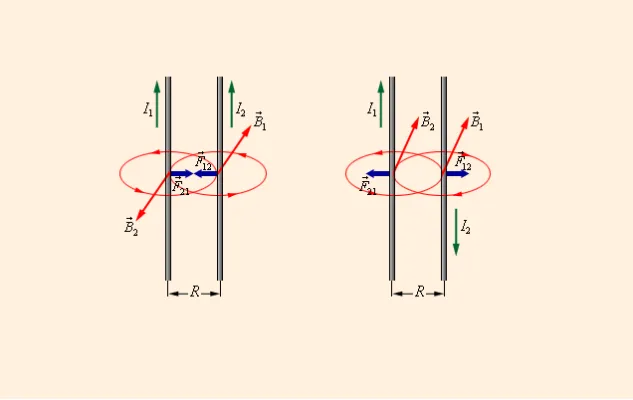
На рисунке 2 показано взаимное упорядочение векторов \\\\vec\ и \\\\vec\ для положительно заряженной частицы.
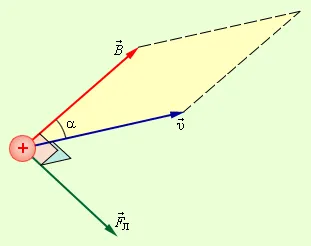
Рисунок 2.
Мера силы Лоренца, \\\\vec_\, равна площади параллелограмма, образованного векторами \\\\vec\ и \\\\vec\, умноженными на заряд q.
Сила Лоренца нормальна, т.е. перпендикулярна векторам \vec\ и \vec\.
Работа, совершаемая силой Лоренца, всегда равна нулю, так как эта сила всегда перпендикулярна скорости и перемещению груза. Величина скорости не меняется под воздействием магнитного поля, его влияние приводит только к изменению направления скорости. Поэтому заряженная частица, движимая силой Лоренца перпендикулярно магнитному полю, имеет круговой путь, если она однородна и ее скорость лежит в плоскости, перпендикулярной вектору \\\\vec\. Радиус можно рассчитать по следующей формуле:
В таких случаях магнитная сила Лоренца действует как центростремительная сила. Это показано на рисунке. 3.
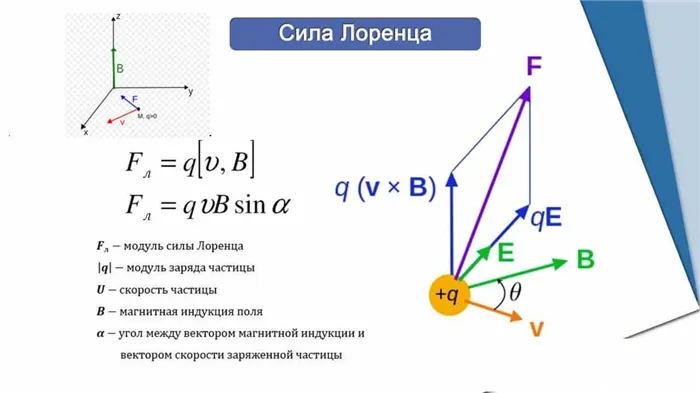
Рисунок 3: Круговое движение заряженной частицы в однородном магнитном поле.
Период кругового движения частицы в однородном магнитном поле можно определить по следующей формуле:
\T=2 \pi R u=2 \pi m q B\
Это выражение подтверждает, что заряженные частицы с определенной массой m не зависят от скорости u и радиуса кругового пути R.
Применение силы Лоренца
Для определения угловой скорости кругового движения заряженной частицы применяется следующая формула:
\\omega=u R=u q B m u=q B m\
Частота, с которой заряженная частица вращается в однородном магнитном поле, называется циклотронной частотой. Она не зависит ни от скорости, с которой движется частица, ни от ее кинетической энергии.
Это условие позволяет применять силу Лоренца к циклотронам и особенно к ускорителям тяжелых частиц, таких как ионы и протоны. На рисунке 4 показано схематическое изображение циклотрона.
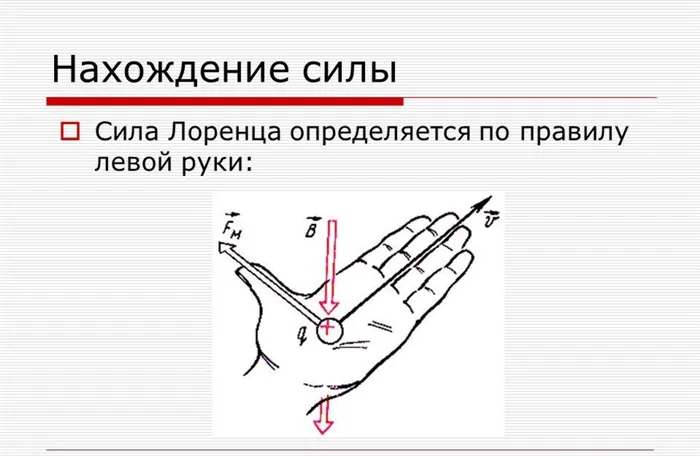
Рисунок 4: Траектория движения заряженных частиц в вакуумной камере циклотрона.
Дуант — это один из двух полых металлических полуцилиндров, расположенных в вакуумной камере циклотрона между двумя полюсами электромагнита в качестве ускоряющего электрода D. Дуант является проводником.
Проводники подвергаются переменному электрическому напряжению, частота которого соответствует частоте циклотрона. Заряженные частицы вводятся в центр камеры. Электрическое поле, созданное в зазоре между двумя проводниками, ускоряет движение частиц. При движении вдоль полукругов на них действует сила Лоренца. Увеличение энергии частиц приводит к увеличению радиуса полукругов. Электрическое поле заставляет заряженные частицы ускоряться, а магнитное поле удерживает их на определенной орбите. Энергия ускорения протонов в циклотронах может достигать 20 МэВ.
Однородные магнитные поля используются в различных устройствах, особенно в масс-спектрометрах.
Устройства позволяют разделять изотопы — ядра, имеющие одинаковый заряд, но разную массу. Например, 20 Ne, 22 Ne.
Простой масс-спектрометр показан на рисунке 5.
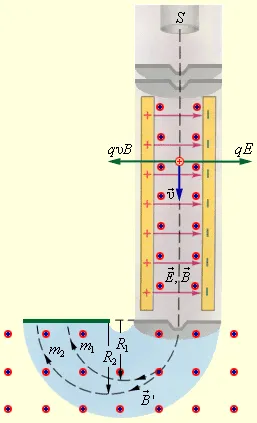
Рисунок 5. Селектор скорости и масс-спектрометр.
Ионы, выходящие из источника S, проходят через множество маленьких отверстий и образуют узкий пучок. После входа в селектор скорости они продолжают движение в альянсе однородного электрического поля, сформированного в зазоре между пластинами плоского конденсатора, и магнитного поля, сформированного в зазоре между разноименно заряженными полюсами электромагнита. Направление начальной скорости \vec\ заряженных частиц перпендикулярно векторам \vec\ и \vec\.
Когда частица движется в области пересечения электрического и магнитного полей, на нее действует электрическая сила \\\\vec\ и магнитная сила Лоренца. Если выполняется условие E = uB, то влияние этих сил полностью компенсируется. Это приводит к равномерному и линейному движению частицы. После прохождения конденсатора он направляется через отверстие экрана. Отделение частиц, движущихся с \u=\frac от селектора
В результате этих процессов частицы с эквивалентной скоростью оказываются в однородном магнитном поле \\vec\ – в камере масс-спектрометра. Сила Лоренца, воздействуя на частицы заставляет их двигаться в камере, в плоскости перпендикулярной магнитному полю по траекториям, в виде окружностей с радиусами \\mathrm=\frac>\.
Здесь магнитная сила обозначается через B, заряд частицы через q, напряженность электрического поля через E, а скорость движущейся частицы через v.
Содержание
Заряженная частица
Сила Лоренца f, действующая на заряженную частицу (с зарядом q ), находящуюся в движении (с постоянной скоростью v ). Поле E и поле B изменяются в пространстве и времени.
Сила F, действующая на частицу с электрическим зарядом q, движущуюся с постоянной скоростью v, во внешних электрическом поле E и магнитном поле B, равна
+ \mathbf \times \mathbf)» width=»» height=»» />
где × это векторное произведение. Все величины, выделенные жирным шрифтом, являются векторами. Более подробно:
(t,q) = q\mathbf(\mathbf,t) + \mathbf<\dot> \times \mathbf(\mathbf,t)» width=»» height=»» />
где r — радиус-вектор заряженной частицы, t — время, а точка — производная по времени.
Непрерывное распределение заряда
Сила Лоренца (на единицу объема) f, действующая на непрерывное распределение заряда (плотность заряда ρ) в движении. Плотность потока 3 J соответствует движению заряженного элемента dq в объеме dV .
Для непрерывного распределения заряда сила Лоренца имеет вид:
+ \mathbf \times \mathbf\right)\,\!» width=»» height=»» />
Где d F — сила, действующая на малый элемент dq .
Направление движения частицы как функция ее заряда, когда вектор магнитной индукции перпендикулярен вектору скорости (для нас, рассматриваемых из плоскости рисунка, перпендикулярен ему).
В однородном магнитном поле, перпендикулярном вектору скорости, заряженная частица равномерно движется по окружности постоянного радиуса под действием силы Лоренца
| GHS | SI |
|---|---|
| vB\Rightarrow r = |
\cdot |
Работа, совершаемая силой Лоренца, равна нулю, поскольку векторы силы и скорости всегда ортогональны. Скорость не зависит от
| GHS | SI |
|---|---|
Если заряженная частица движется в магнитном поле так, что вектор скорости » width=»» height=»» /> Угол и наклон
| GHS | СИ |
|---|---|
| » width=»» height=»» />, \cdot v\cos\alpha» width=»» height=»» /> | » width=»» height=»» />, \cdot v\cos\alpha» width=»» height=»» /> |
Применение силы Лоренца


Пучок электронов, движущийся по круговой траектории под воздействием магнитного поля. Освещение происходит за счет возбуждения атомов остаточного газа в цилиндре.
В электроприборах
Основное применение силы Лоренца (или ее частного случая, силы Ампера) — это электрические машины (электродвигатели и генераторы). Сила Лоренца часто используется в электронных устройствах для воздействия на заряженные частицы (электроны и иногда ионы), например, в телевизионных электронно-лучевых трубках, а также в масс-спектрометрии и МГД-генераторах.
В ускорителях заряженных частиц
Сила Лоренца также используется в ускорителях для заряженных частиц и определяет траекторию, по которой движутся эти частицы.
В вооружении
- См. рельсотрон, или, как его ещё называют, рэйлган («рельсовая пушка»)
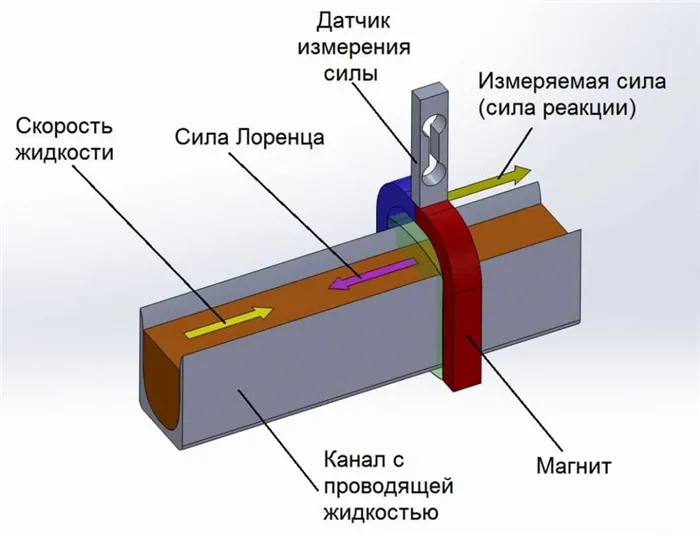
Другие применения
- Бесконтактное измерение скорости движения проводящей жидкости (Велосиметрия силой Лоренца).








