Расчёт ёмкости конденсатора. Электроемкость измеряется в чем

Такой подход улучшает схему, поскольку пульсации значительно «сглаживаются», а напряжение пробоя не пробивается за пределы значения.

Что такое электрическая емкость и в чем она измеряется

В электротехнике часто встречается понятие емкости. Это относится к электрической емкости проводников, батарей и конденсаторов, а не ведер или других емкостей. Не путайте их. В этой статье разъясняется, что такое электрическая емкость, от чего она зависит и в каких единицах измеряется.

В случае проводников электрическая емкость — это величина, описывающая способность объекта накапливать электрический заряд. Это его естественное значение. Он обозначается латинской буквой C. Она равна отношению нагрузки к потенциалу. В математической форме это можно записать следующим образом.

Емкость каждого объекта зависит от его формы и геометрических размеров. Рассматривая в качестве примера сферический проводник, формула для его величины выглядит следующим образом

Этот тип применяется к одному проводнику. Если два проводника поместить рядом друг с другом и разделить их диэлектриком, образуется конденсатор. Это будет объяснено позже, а пока давайте рассмотрим, как измеряется электрическая емкость.

Единицей измерения электрической емкости является фарад. При анализе на компоненты в соответствии со следующей формулой

1 фарад = 1 Кл/1 В.

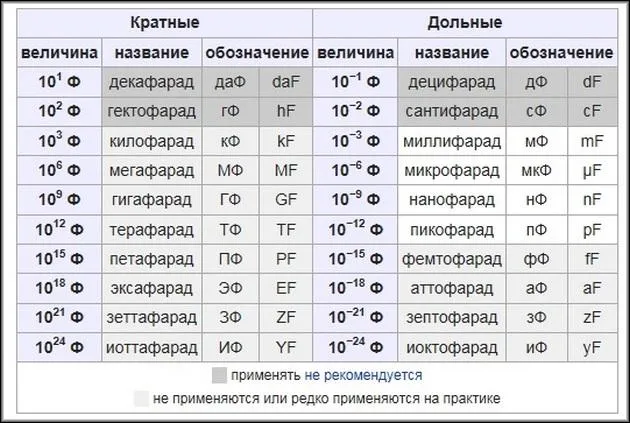
Исторически сложилось так, что размер этого подразделения не совсем корректен. Важно отметить, что на практике приходится иметь дело со значениями электрической емкости (мили, микро, нано- и пикофарады). Это соответствует долям фарад, как показано ниже.

1 мФ = 10 ^(-3) Ф

1 мкФ = 10 ^(-6) Ф

1 нФ = 10 ^(-9) Ф

1 пФ = 10 ^(-12) Ф

Конденсаторы

Конденсатор — это две пластины из проводящего материала, расположенные друг напротив друга, между которыми находится слой диэлектрика. Когда они заряжены, обкладки имеют разные потенциалы: одна — положительный, другая — отрицательный. Емкость конденсатора зависит от размера и разности потенциалов обкладок нагрузки и напряжения между ними. Между пластинами создается электростатическое поле, и заряд удерживается в катушке. Формула для емкости конденсатора в общем случае:.

Проще говоря, емкость конденсатора зависит от площади пластин, расстояния между ними и относительной диэлектрической проницаемости материала между ними. Они отличаются используемым диэлектриком.

• керамические;
• плёночные;
• слюдяные;
• металлобумажные;
• электролитические;
• танталовые и пр.

Поскольку формула для площади фигуры зависит от ее геометрии, формула для ее емкости также отличается в каждом случае.

Для уровней конденсаторов:.

Для двух концентрических сфер с общим центром:.

Для цилиндрических конденсаторов:.

Как и другие компоненты электрической цепи, существует два основных способа соединения конденсаторов: параллельное и последовательное.

От этого зависит конечная электрическая емкость результирующей цепи. Расчет емкости различных конденсаторов аналогичен расчету сопротивления резисторов различных соединений, за исключением того, что уравнения для методов соединения меняются местами.

1. При параллельном соединении общая электроемкость цепи является суммой емкостей каждого из элементов. Каждый следующий подключенный увеличивает итоговую емкость

1. При последовательном подключении электроемкость цепи снижается, подобно снижение сопротивления в цепи параллельно включённых резисторов. То есть:

Кобб = (1 / C1) + (1 / C2) + (1 / C3)

Важно: В параллельной цепи напряжение на клеммах каждого компонента одинаково. Это используется для достижения более высоких значений емкости. При последовательном соединении двух компонентов напряжение на каждой обмотке конденсатора составляет половину общего напряжения. Три последующих, одна третья и так далее.

Аккумуляторы и электроемкость

Основными функциями аккумуляторной батареи являются.

В этом случае значение емкости используется для количественной оценки времени работы или, проще говоря, для расчета срока службы батареи.

Для батарей используются следующие размеры для описания электрической емкости.

• А*ч — ампер-часы для больших аккумуляторов, например автомобильных.
• мА*ч — милиампер-часы, для аккумуляторов для носимых устройств, например смартфонов, квадрокопетров и электронных сигарет.
• Вт*часы — ватт-часы.

Эти характеристики позволяют определить срок службы батареи при определенной нагрузке. Электрическая емкость батареи измеряется в кулонах (Кулонах). Кулоб равен количеству электроэнергии, переданной в аккумулятор при интенсивности 1a за одну секунду. Затем, при пересчете на время, за один час при токе 1а переносится 3 600 КИ.

Одним из способов измерения емкости батареи является разряд батареи знакомым током и измерение времени разряда. Например, если аккумулятор разряжается до низкого уровня напряжения за 10 часов при токе 5а, то его емкость составляет 50 а*ч.

Электрическая емкость — это величина электронов и электричества. На практике конденсаторы используются почти во всех электронных схемах. Например, в источниках питания для нормализации пульсаций и снижения воздействия высокого напряжения на силовые ключи. Со временем схемы различных цепей и ШИМ-контроллеров определяют частоту. Батареи также используются в широком спектре приложений. В целом, задачи накопления энергии и хранения фазы очень распространены.

Представленный видеоролик помогает подробно раскрыть тему.

Видео содержит краткое описание.

Теперь вы знаете, что такое мощность, в каких единицах она измеряется и от чего зависят цены. Мы надеемся, что вы найдете эту информацию полезной и понятной.

Электрическое сопротивление определяется как отношение $ r $ между напряжением $ u $ и непрерывным током $ i $ в цепи по закону Ома.

Конденсатор

Прежде чем мы сможем понять, что такое емкость простого конденсатора, нам необходимо определить, что такое электрический элемент. Конденсатор — это беспроводной электронный компонент, способный накапливать и отдавать определенное количество заряда. Он состоит из следующих элементов

1. Корпуса. Зачастую выполняется из алюминия. По форме он может быть плоским, сферическим и цилиндрическим.
2. Обкладок (2 и более). Их делают из металлических пластинок или фольги.
3. Диэлектрической прокладки. Устанавливается между обкладками и служит в качестве изолятора.
4. Двух или более выводных контактов для подключения устройства в электроцепь.

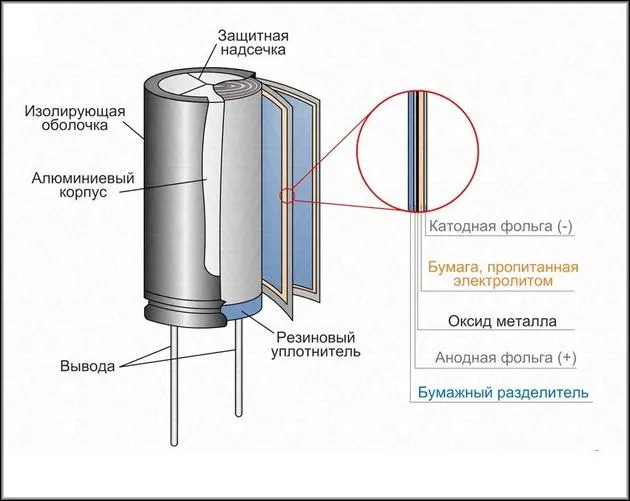
Такой аккумулятор электрической нагрузки функционирует следующим образом

1. В момент подключения элемента к источнику электрического тока, он выступает в роли проводника. В этот момент электроток имеет максимальное значение, а напряжение — минимальное.
2. На обкладках элемента начинают скапливаться положительные и отрицательные заряды (электроны и ионы). Таким образом происходит зарядка самого устройства. На момент заряда сила электротока постепенно уменьшается, а напряжение наоборот — увеличивается.
3. После того как количество заряда в конденсаторе станет больше допустимого предела, он разряжается и процесс опять начинает повторяться циклически.

Мощность является основой производительности этого устройства. Этот параметр определяет время накопления заряда и общую «емкость» устройства. Следующая диаграмма помогает понять, как простой конденсатор выделяется в электрической схеме.

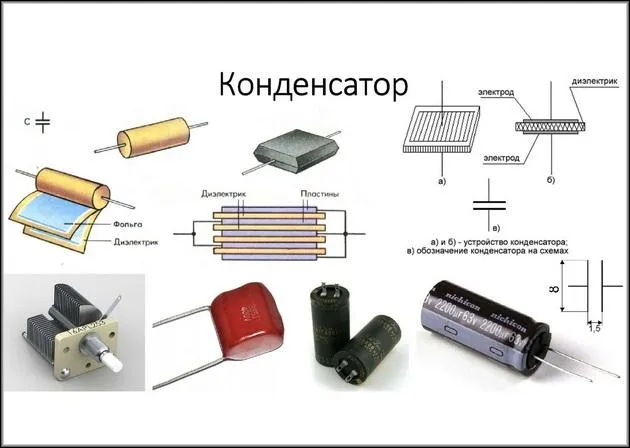
Электрическая емкость, как и сам конденсатор, нашла широкое применение. Используется для:.

1. Частотных фильтров.
2. Источника импульсов для различной фотоаппаратуры.
3. Сглаживателей пульсирующих токов в выпрямителях.
4. Фазосдвигающих элементов для электрических двигателей.

Использование конденсаторов в различных приложениях основано именно на способности макета накапливать заряд. В более сложном электрооборудовании эти устройства используются для постоянного поддержания определенных тенденций в различных устройствах хранения данных.

Емкость

Емкость конденсаторов — это натуральная величина, определяющая причину между спиральным накопительным грузом и разностью потенциалов между ними.

В системе СИ емкость конденсатора и его единица измерения — фарад. Для его обозначения используется буква F. Однако в фарадах емкость конденсатора измеряется редко, так как он значительно выгоднее по цене. Чаще всего используются кратные доли емкости конденсатора.

Цены на емкости конденсаторов всегда обозначены на корпусе устройства.

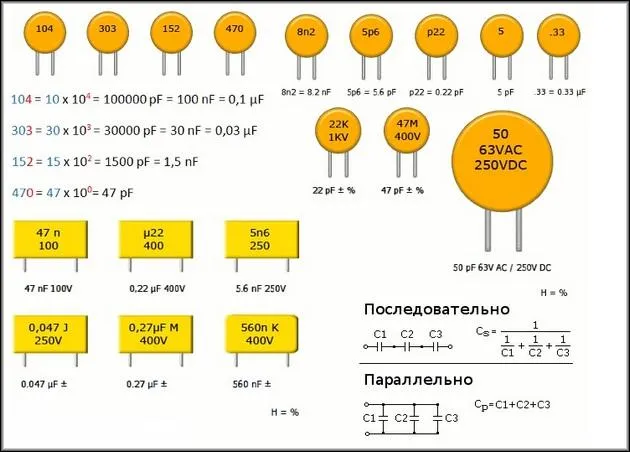
На схеме элементы обозначены буквой ‘C’. Определение емкости необходимо для упрощения процесса выбора электродов, необходимых для схемы.

Зависимость

Благодаря приведенному выше объяснению вы узнали, что такое емкость. Далее мы рассмотрим, от чего зависит эта функция. Емкость конденсатора зависит от расстояния между обкладками, площади обкладок и самого диэлектрика. Это показывает, от чего зависит емкость устройства: она прямо пропорциональна площади пластин конденсатора и обратно пропорциональна расстоянию между пластинами.

Давайте посмотрим, как найти эту цену. Для уровней конденсаторов формула емкости имеет вид

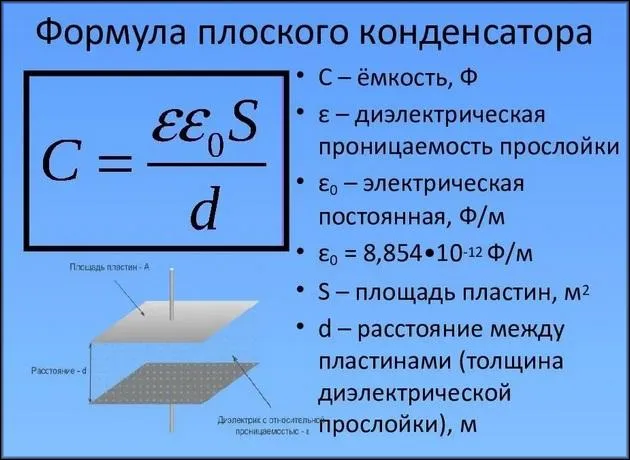
Способность устройства накапливать нагрузки на поверхности покрытия и зависимость от толщины диэлектрического слоя показывают, что габаритные размеры элемента также влияют на эту величину.

Возьмем вторую кожу, где нагрузка на эту область достаточно мала, чтобы считать ее точкой. Этот груз с силой тянет за собой первая крышка

Электроемкость конденсатора

Логично предположить, что разные конденсаторы накапливают заряд по-разному. Как можно охарактеризовать эту функцию устройства? У него есть специальная величина — электрическая емкость (или просто емкость) конденсатора.

Чтобы понять важность этой величины, давайте рассмотрим эксперимент. Возьмите две металлические пластины и положите их на изолированное основание лицом друг к другу.

Подключите потенциометр к пластинам. Это устройство (рис. 4) по конструкции и принципу действия похоже на электрический детектор. Он может регистрировать значение напряжения, возникающего между пластинами.

Поэтому одну из пластин (A) соедините кабелем со стержнем потенциометра, а другую (B) — с корпусом устройства (заземлением). Прикоснитесь к надежно заряженной стеклянной палочке на внешней стороне пластины A (рис. 5).

На пластину A подается положительный заряд $3500q. Теперь вокруг этого заряда (пластина A) существует электрическое поле. Это действие приводит к перераспределению нагрузки на пластину B, при этом отрицательная нагрузка перемещается к внутренней стороне пластины, а положительная — к внешней.

Помните, что пластина B заземлена? Это заставляет свободные электроны перемещаться от земли к пластине. Они нейтрализуют положительный заряд на внешней стороне пластины. Таким образом, вы получили отрицательный заряд $ -q $ на пластине B (рис. 6). Его величина такая же, как и нагрузка на другие пластины.

Игла потенциометра отклоняется. Запишите это значение напряжения между пластинами. Затем снова приложите к пластине B нагрузку такого же размера, как и первая нагрузка. Затем добавьте одну треть и одну четверть такого заряда, наблюдая за иглой потенциометра.

При увеличении нагрузки в 2, 3 или 4 раза показания потенциометра и напряжение между пластинами увеличиваются в 2, 3 или 4 раза соответственно. В этом случае отношение нагрузки к напряжению остается постоянным: $ \ frac = \ frac = \ frac =const$.

Теперь можно определить емкость конденсатора.

Емкость конденсатора — это величина, измеряемая как отношение заряда на одной из пластин конденсатора к напряжению между пластинами: $ C = \ frac$.

Единицы измерения электроемкости

В СИ емкость измеряется в фарадах ($ F $).

Емкость конденсатора равна 1, когда напряжение 400 ⬃ пробела V$ при заряде 400 ⬃ пробела Cl$ (рис. 7): 400 ⬃ пробел F = \frac$.

Эта единица измерения названа в честь английского естествоиспытателя Майкла Фарадея (рис. 8).

Рисунок 8.Майкл Фарадей (1791-1867) — английский физик-экспериментатор.

Емкость 400 \пространств f $ настолько высока, что на практике используются дробные единицы ($ µf $) и пикофарады ($ pf $).

Зависимость электроемкости от площади пластин конденсатора

От чего зависит мощность? Начните с размера вафель.

Запишите значения напряжения $ U_1 $, полученные в первом эксперименте, используя электрометр и конденсатор. Затем возьмите тарелку с большей поверхностью. Дайте ему точно такую же нагрузку $ q (рис. 9).

Видно, что игла электрометра отклоняется не очень сильно. Это означает, что напряжение между этими пластинами меньше, чем напряжение между меньшими пластинами ($ u_1> u_2 $).

Из определения силовой емкости: $ c_1 = \ frac $, $ c_2 = \ frac $, $ c_2> c_1 $.

Чем больше поверхность пластины, тем больше емкость конденсатора.

Однако это создание системы заряженных тел. Это мало взаимодействует с окружающими телами, даже если на них создаются значительные нагрузки. Затем мы можем снова поговорить о емкости, но на этот раз о емкости этой трубопроводной системы.

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. Это может быть воспринято на собственном опыте. Когда конденсатор заряжен и присоединен к лампе (поскольку конденсатор достаточно большой), лампа будет светиться в течение некоторого времени.

Таким образом, энергия накапливается в заряженном конденсаторе и высвобождается при его разрядке. Легко видеть, что эта энергия является потенциальной энергией взаимодействия обкладок конденсатора.

Затем мы можем рассчитать эту энергию, чтобы лучше понять происхождение энергии заряженного конденсатора.

Начните с плоского воздушного конденсатора. Ответьте на следующие вопросы. Какова сила притяжения его оболочки между его Используйте один и тот же размер. Нагрузка конденсатора, поверхность пластины.

Возьмем вторую кожу, где нагрузка на эту область достаточно мала, чтобы считать ее точкой. Этот груз с силой тянет за собой первая крышка

Где находится сила первого поля одеяла:.

Направление этой силы параллельно линиям поля (т.е. перпендикулярно пластине).

Результирующая сила притяжения второго одеяла представляет собой сумму всех сил, с которыми все возможные малые грузы второго одеяла притягиваются к первому одеялу. При таком суммировании из скобки убирается постоянный множитель, дающий каждый в суммируемой скобке. Результат следующий.

Предположим, что расстояние между обложками было изменено от первоначальной цены до конечной. В этом случае работает притяжение пластин.

Знак правильный. Сила действует положительно, потому что пластины притягиваются друг к другу по мере сближения. Напротив, удаление пластины d_1) ‘alt ='(d_2> d_1) ‘/> требует работы с угольной энергией.

Учитывая типы (11) и (7), существует

Это можно сформулировать следующим образом.

Доказано, что работа потенциального притяжения бытовки равна изменению с отрицательным знаком. Отсюда следует, что — потенциальная энергия взаимодействия электродов или энергия заряженного конденсатора.

Используя уравнение типа (12), можно получить еще два вида энергии конденсатора (смотрите сами!) :.

Особенно полезны типы (12) и (14).

Теперь предположим, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью. Мощность тяги уменьшается на один коэффициент, и вместо (11) имеем

Расчет проекта мощности легко узнаваем, значения входят в емкость, а виды (12) — (14) остаются неизменными. Емкость конденсатора выражается прессом (10).

Таким образом, типы (12) — (14) являются католическими. Они применимы как к воздушным, так и к наборным конденсаторам.

Энергия электрического поля

Вычислив энергию конденсатора, мы обещали более глубокую интерпретацию происхождения этого действия. Итак, начнем.

Рассмотрим воздушный конденсатор и преобразуем тип (14) для его энергии.

Но это объем конденсатора. Мы получаем:.

Посмотрите внимательно на этого человека. В конденсаторе нет ничего особенно важного! Мы видим, что энергия электрического поля сосредоточена в объеме.

Энергия конденсатора — это энергия электрического поля, заключенного в нем.

Поэтому электрическое поле само по себе обладает энергией. Здесь нас ничто не удивляет. Радиоволны, солнечный свет являются примером распространения энергии, переносимой в пространство с помощью электромагнитных волн.

Эта величина, энергия на единицу объема поля, называется объемной плотностью энергии. Введите (15), чтобы:.

Этот тип не включает геометрические размеры. Она дает наиболее четкую связь между энергией электрического поля и его напряженностью.

Если конденсатор заполнен диэлектриком, его емкость увеличивается с возрастом и вместо него используются типы (15) и (16).

Как видите, энергия электрического поля также зависит от диэлектрической проницаемости среды, в которой находится поле. Стоит отметить, что типы, отобранные по энергии и плотности энергии, значительно превосходят электростатические. Это относится не только к электростатическим полям, но и к изменяющимся во времени электрическим полям.