Как правило, типы тонких линз записываются следующим образом. Сумма инверторов расстояний от объекта до линзы, сумма расстояний от линзы до изображения равна обратной величине фокусного расстояния.
Тонкие линзы. Построение изображений.
Использование кода: изготовление изображений линз, тонкие типы линз.
Правило маршрута лучей света в тонких линзах, сформулированное в предыдущем выпуске, приводит к самому важному утверждению.
Теорема об образе. Если перед линзой находится яркая точка, то после преломления линзы все лучи света (или их продолжение) пересекаются в одном и том же месте.
| Напомним ещё раз, что это касается не вообще всех лучей, а только параксиальных, то есть образующих малые углы с главной оптической осью. В предыдущей теме мы договорились, что рассматриваем только параксиальные лучи. Лишь для них работают наши правила хода лучей сквозь тонкие линзы. |
Точка называется образом точки.
Если сами преломленные лучи пересекаются в этой точке, изображение называется действительным. Лучи видны на экране, потому что энергия лучей сосредоточена в этой точке.
Если преломленный луч пересекает точку, но его непрерывность (это происходит, когда преломленный луч отклоняется после линзы) называется иллюзорной. Энергия не концентрируется в точке и поэтому не может быть получена на экране. Фантастические образы появляются благодаря состоянию нашего мозга. Сфокусируйте ветвящиеся лучи на иллюзорном перекрестке и покажите, что видите светлое место на этом перекрестке. Фантастический образ существует только в нашем сознании.
Теорема об изображении служит основой для создания изображений с тонкими линзами. Докажите теорему для аспирированных и диффузных линз.
Собирающая линза: действительное изображение точки.
Сначала рассмотрим изогнутые линзы. Как минимум — расстояние пятна от объектива, фокусное расстояние объектива. Есть два радикально разных случая. И (и промежуточный случай). Мы рассмотрим эти случаи один за другим, каждый из которых описывает характеристики точечного источника и изображение более широкого объекта.
Первый случай:. Прожектор находится дальше от линзы, чем левая фокальная плоскость (рис. 1).
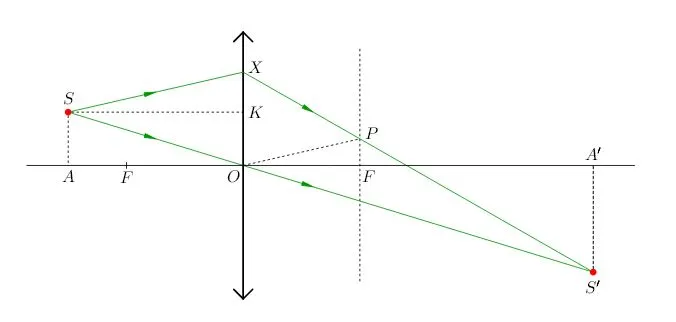 |
| Рис. 1. Случай a>f: действительное изображение точки S |
Радиус, проходящий через зрительный центр, не преломляется. Возьмите любой радиус и постройте точку пересечения преломленного радиуса с радиусом, показав, что положение точки не зависит от выбора радиуса (другими словами, точка одинакова для всех лучей). Таким образом, после пересечения линз преломления в точке и доказательства теоремы об образе все лучи выходят.
Точка находится путем планирования дальнейшего хода радиуса. Мы знаем, как это сделать: проводим визуальную ось, параллельную лучу, в месте ее пересечения с уровнем фокуса падающего фокуса и преломляем луч до разреза в луче.
Теперь мы ищем расстояние от точки до линзы. Расстояние определяется только и, то есть положением источника и свойствами линзы, так что расстояние дается только и не зависит от конкретного луча.
Перпендикулярно главной визуальной оси. Также спроектируйте его параллельно главной зрительной оси, т.е. перпендикулярно линзе. Вы получаете три набора подобных треугольников.
В результате получается следующая цепочка равенств (количество типов над символом равенства указывает на то, что пара одинаковых треугольников приводит к этому равенству).
Однако соотношение (4) переписывается в виде.
Таким образом, существует необходимое расстояние от точки до линзы.
Как видите, это не зависит от выбора балки. Поэтому все радиусы после преломления линзы проходят через точку, которую мы сделали. Эта точка будет истинным изображением источника.
В этом случае доказывается теорема об образе.
Практическая важность теоремы об образах заключается в следующем. Все лучи источника пересекаются после линзы в какой-то точке, поэтому достаточно получить два луча, которые наиболее подходят для построения изображения — его идолов. Какие два?
Если источник находится не на главной зрительной оси, то подходят следующие лучи
— Радиус, проходящий через зрительный центр линзы — без преломления — и радиус, параллельный главной зрительной оси, после прохождения преломления через камин.
Структура изображения с этими лучами показана на рисунке 2.
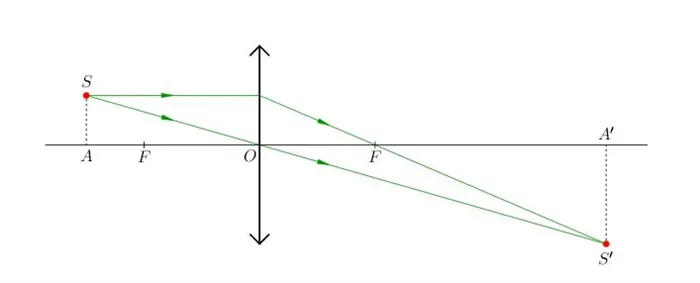 |
| Рис. 2. Построение изображения точки S, не лежащей на главной оптической оси |
Если точка находится на главной визуальной оси, подходит только один радиус, который перемещается вдоль главной визуальной оси. Второй радиус должен быть «неловким» (рис. 3).
Собирающая линза: действительное изображение предмета.
Рассмотрим изображение объекта. Напомним, что мы все еще находимся в этом случае. Можно выделить три характерные ситуации.
1. Изображение объекта является реальным, перевернутым и увеличенным (рис. 4, показан двойной фокус). Тип объектива не является фактором, определяющим, является ли он таковым (почему?) так и есть.
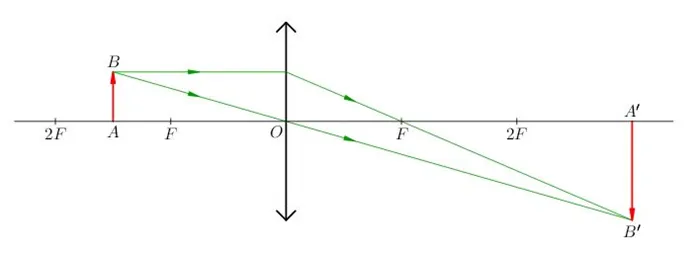 |
| Рис. 4. : изображение действительное, перевёрнутое, увеличенное |
Такая ситуация возникает, например, при включенных фарах на слайдах и фарах в фильмах. Эти визуальные средства дают на экране эффектное изображение того, что происходит в фильме. Если вы когда-либо представляли слайды, то знаете, что для того, чтобы слайд появился на экране, его нужно ввести вверх ногами, а не вверх ногами.
Причина приведения размера изображения к размеру объекта называется линейным расширением линзы и обозначается G- (это заглавная буква греческого «гамма»).
В зависимости от схожести треугольников, в зависимости от
Тип (8) используется во многих задачах, где имеет место линейное увеличение линзы.
2 … В данном случае тип (6) указывает на это. ( Линейное расширение линзы, обусловленное (8), является унитарным. Это означает, что размер изображения равен размеру объекта (рис. 5).
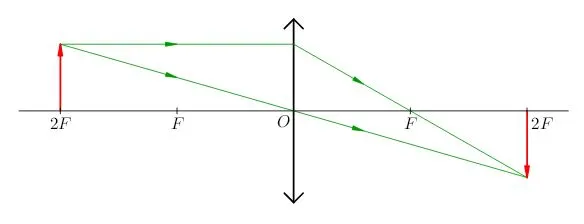 |
| Рис. 5.a=2f: размер изображения равен размеру предмета |
3 … В данном случае тип объектива указывает на то, что (почему?). Линейное увеличение линзы меньше единицы — изображение получается реальным, перевернутым и уменьшенным (рис. 6).
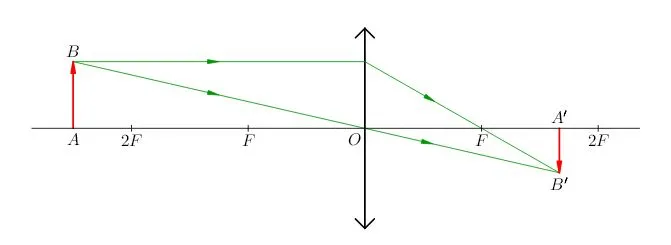 |
| Рис. 6.a>2f: изображение действительное, перевёрнутое, уменьшенное |
Это общая проблема для многих визуальных приборов. Для изображения удаленных объектов используются камеры, бинокли, телескопы, короче говоря, объективы. Когда объект удаляется от линзы, его холостой размер уменьшается, и он перемещается ближе к фокальной плоскости.
Проверка первого дела завершена. Перейдем ко второму случаю. Он не обладает большой вместимостью.
Линзы являются коллекционными и могут быть разбросаны. Рассеивающие линзы, с другой стороны, тоньше в центральной части, в то время как коллекционные линзы толще в центре, чем по краям.
Построение изображения в линзах
Вы уже знаете, что линза — это прозрачное тело, которое фокусирует (собирает) или рассеивает. Но каковы свойства изображения, создаваемого линзой, и можно ли сделать его таким же, как у зеркала?
Основная функция линзы в зрительной системе заключается в фокусировке или рассеивании входящих лучей света симметрично вокруг оптической оси (см. рис. 1). В случае круглого театра или амфиктилоса зрительная ось — это линия, соединяющая центры сфер, определяющих линзу. Эта ось также является осью симметрии объектива.
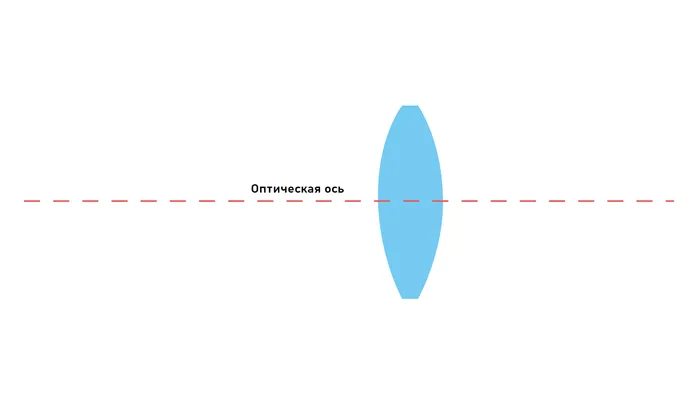
Рисунок.
Зрительная ось определяет центр линзы. Графически линза показана на рисунке 2 ниже.
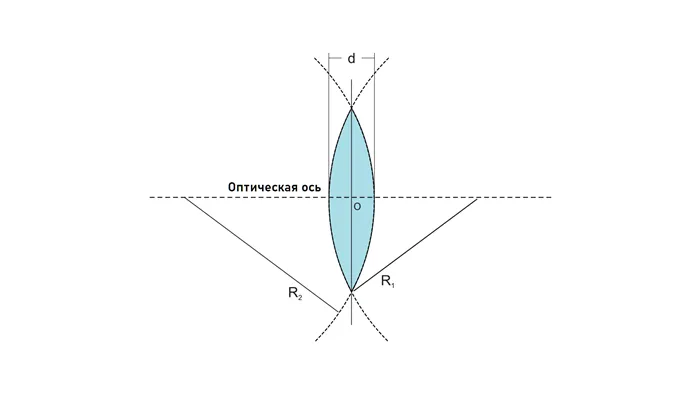
Рис. 2. Как определить центр выпуклой линзы.
Свет дважды изгибается при прохождении через линзу: один раз при входе в линзу и второй раз при выходе из нее.
Когда лучи света, идущие параллельно зрительной оси, проходят через собирающую линзу, они пересекаются в точке на зрительной оси. Эта точка называется фокусной точкой объектива и обозначается F. Расстояние этой точки от центра S линзы называется фокусным расстоянием F (см. рис. 3).
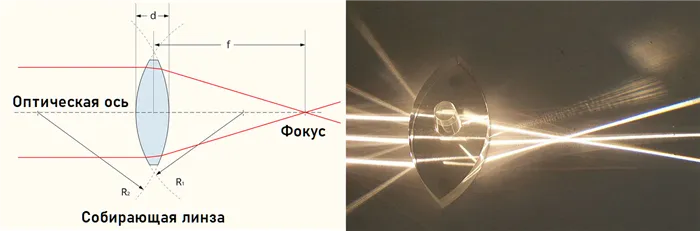
Рис. 3. Фокус F и фокусное расстояние F амбиентного объектива
ПРИМЕЧАНИЯ. Фокусная точка (F) фокусирующей линзы — это точка пересечения всех лучей света после их прохождения из линзы и параллельно зрительной оси перед входом в линзу.
Фокусное расстояние (f) объектива — это расстояние от фокуса (F) до центра линзы.
В случае большого мышления падающий пучок света отклоняется — лучи света, попадающие в линзу, мыслят о своем продолжении в одной точке. Это называется великим сосредоточением многих мыслей (см. рисунок 4). Он находится на той же стороне, что и источник линзы.

Рисунок 4. Средоточие многих мыслей
Как формируется изображение с помощью собирающей линзы?
Чтобы увидеть, какое изображение можно получить с помощью монтажного объектива, давайте проведем эксперимент.
Эксперимент 1: Наблюдайте за изображением, создаваемым линзой.
Что вам нужно?
- фонарик;
- кусок черного картона размером больше стекла фонарика;
- ножницы;
- скотч (липкая лента);
- большая лупа;
- белая картонная коробка (экран).
- Вырежьте стрелку в черной картонной коробке.
- С помощью скотча приклейте черный картон к экрану фонарика.
- Расположите лупу, фонарь и экран на оптической оси лупы.
- Измените положение фонаря и экрана для получения четкого изображения.
Какие выходы доступны?
Изменяя положение экрана и линзы по отношению к лупе, можно получить различные изображения: одно увеличенное, уменьшенное, перевернутое, прямое. Как вы знаете, централизованная линза не обязательно увеличивает наблюдаемый объект. Как это произошло?
Как и в случае с зеркалами, геометрические изображения с лучами света (см. рис. 5) помогают ответить на вопросы, поставленные в кратком изложении экспериментов, специально посвященных линзам.
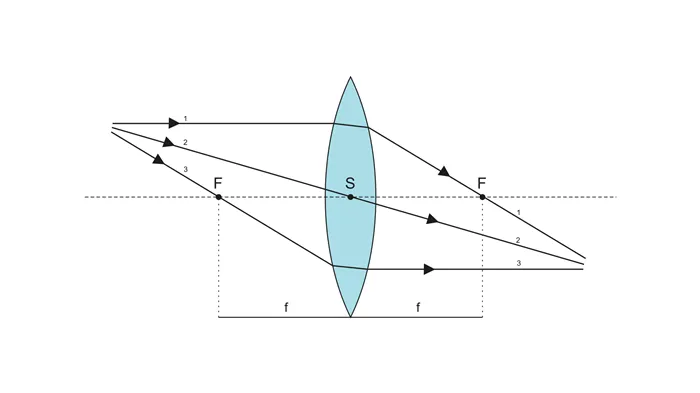
Рисунок 5. Лучи света, используемые для построения изображения на коллекционной линзе
Если необходимо построить изображение с помощью собирающего объектива, обычно выбирают два из трех перечисленных ниже лучей.
- луч, параллельный оптической оси – после прохождения через линзу он проходит через фокус;
- луч, проходящий через центр линзы – после прохождения через линзу его направление (путь) не меняется;
- луч, проходящий через фокусную точку – после прохождения через линзу выходит параллельно оптической оси.
Последнее утверждение относится к тонкой линзе, использованной в эксперименте. Затем толщина линзы игнорируется и рисуется в виде линии, заканчивающейся стрелкой.
Изображение точки формируется разрезом как минимум двух лучей или их продолжением.
Положения объектов и положения изображений по отношению к признакам результирующего изображения обобщены в таблице 1 ниже.
| Положение объекта, x | Положение изображения, y | Особенности изображения |
| x > 2f | f < y < 2f | Перевернутое, действительное, уменьшенное |
| x = 2f | y = 2f | Перевернутое, действительное, имеет те же размеры, что и объект |
| 2f > x > f | y > 2f | Перевернутое, действительное, увеличенное |
| x = f | лучи проходят через линзу и параллельны друг другу | Без изображения |
| x < f | изображение появляется на той же стороне, что и объект | Прямое, мнимое, увеличенное |
Таблица 1. Характеристики изображения, создаваемого собирающей линзой
Из таблицы 1 можно сделать вывод, что особенности изображения, формируемого собирающей линзой, зависят от расстояния объекта от линзы.
Как создается изображение при использовании рассеивающей линзы?
Со многими идеями дело обстоит иначе. Лучи, падающие параллельно линзе, расходятся после выхода из линзы. Как и выше, расширение луча было преломлено, чтобы пересечь точку SO -Calcaled Fantastic Pocal Point (см. Рисунок 6).
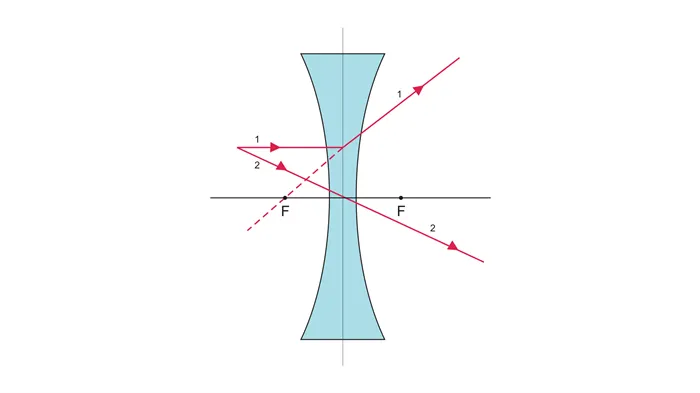
Рисунок 6.Лучи, используемые для построения изображений с помощью пространственных линз.
Рассеивающие объективы (и съемочные объективы) требуют только два луча света для создания изображения.
- падающий луч, параллельный оптической оси – после прохождения через линзу падающий луч движется таким образом, что его продолжение проходит через мнимую фокусную точку;
- луч, проходящий через центр линзы – при прохождении через линзу он не меняет направления.
Помните! Многое продумано до мелочей, и в результате изображение всегда получается прямым, уменьшенным и великолепным.
Линза определяется как прозрачный, однородный материал с плоской поверхностью, сферической поверхностью и двумя преломляющими полированными поверхностями.
Собирающая линза
Если толщина линзы в центре больше, чем по краям, то лучи света, проходящие через линзу, искривляются по зрительной оси. В результате после профилактики такой линзой пучки света, параллельные зрительной оси, концентрируются в точке за линзой в зрительной оси фокальной плоскости.
Если луч падает на линзу, не параллельную оптической оси, он также сходится в точке, но эта точка находится в другой точке фокальной плоскости.
В любом случае луч, падающий на линзу, толщина которой в центре больше, чем по краям, будет сходиться в одной точке. Поэтому такая линза называется собирающей.
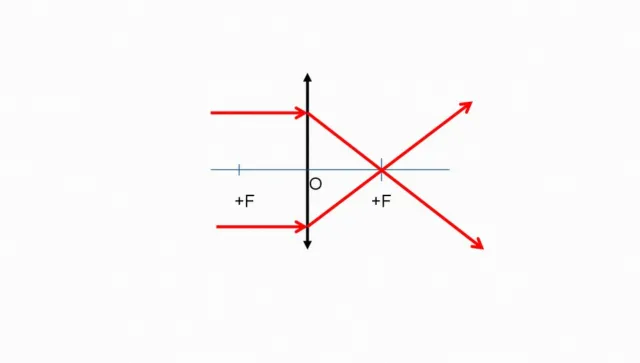
Рис. 2: Путь лучей в сходящейся линзе
Изображение, даваемое собирающей линзой
Чтобы построить изображение точки, заданной линзой, постройте путь лучей в линзе и проследите путь двух произвольных лучей, исходящих из точки. Если лучи пересекаются после прохождения через линзу, то в месте пересечения появляется изображение.
Поскольку лучи, проходящие через сходящуюся линзу, преломляются в направлении главной оптической оси, два луча, выходящие из одной точки, после прохождения через линзу пересекаются и образуют истинное изображение.
Следующие два луча обычно используются для построения изображения точки, полученного с помощью сходящейся линзы:
- луч, проходящий сквозь оптический центр линзы: он не будет преломляться, пройдёт сквозь линзу без изменений;
- луч, перпендикулярный линзе: после прохождения через линзу он будет направлен точно в фокус линзы.
Построив эти два луча, можно найти точку пересечения. Эта точка будет расположена за собирающей линзой и даст истинное изображение. Расстояние до изображения определяется типом тонкой линзы:
Точки O1 и О2 — центры сферических поверхностей, O1o2 — первичная оптическая ось, O — оптический центр, F — первичный фокус, F’ — вторичный фокус, OF’ — вторичная оптическая ось, F — фокальная плоскость.
Изображения, даваемые линзой
Посмотрев этот видеоурок, мы вспомним, что такое линза и для чего она используется. Мы рассмотрим основные характеристики тонких линз. Мы узнаем, как строятся изображения в тонкой линзе. Мы научимся определять характеристики изображений, полученных с помощью тонких линз. Мы также получим формулу для тонкой линзы.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
キットの他のビデオコースにアクセスするには、リストを購入して個人アカウントに追加する必要があります。
Конспект урока «Изображения, даваемые линзой»
В предыдущем уроке мы говорили о том, что линза — это прозрачное тело, ограниченное кривыми (чаще всего сферическими) или кривыми и плоскими поверхностями. Он используется для управления световыми лучами, то есть для изменения направления лучей.
Пока что мы с вами не знаем, как создать изображение предмета в тонкой линзе? На этот вопрос и ответит наш курс.
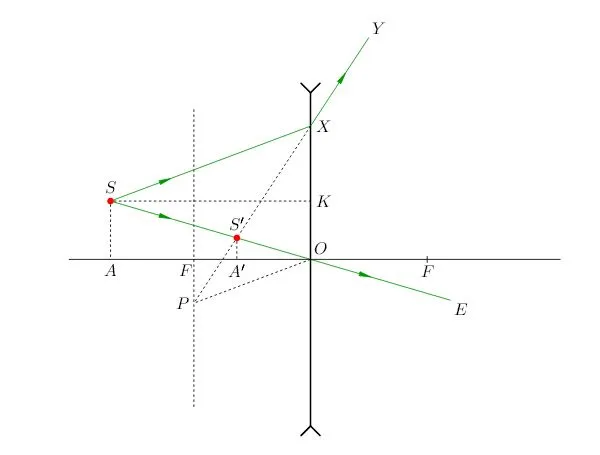
Сначала рассмотрим, как изобразить точечный источник света в монтажно-рассеивающей линзе. Для этого мы в основном будем использовать три «удобных луча» — лучи, путь которых после прохождения через линзу известен заранее:
1) лучи, идущие параллельно главной оптической оси, поскольку после дифракции в линзе они проходят через ее главный фокус (или проходят через ее расширения).
2) Из закона обратимости световых лучей следует, что лучи, проходящие через линзу через ее фокус, после преломления будут двигаться параллельно главной оптической оси — это второй набор лучей.
3) третий набор лучей выбирается в предположении, что лучи, проходящие через оптический центр линзы, не меняют направления.
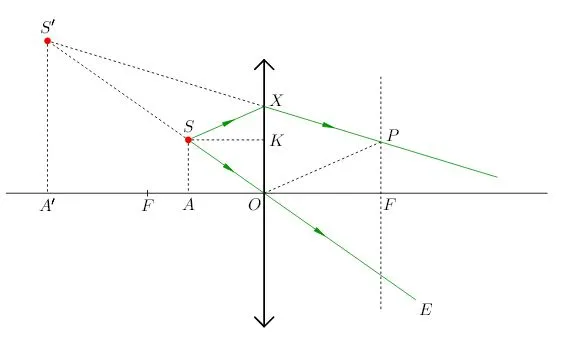
Точка пересечения преломленных лучей на собирающей линзе или их проекций на рассеивающую линзу дает нам положение изображения точечного источника света.
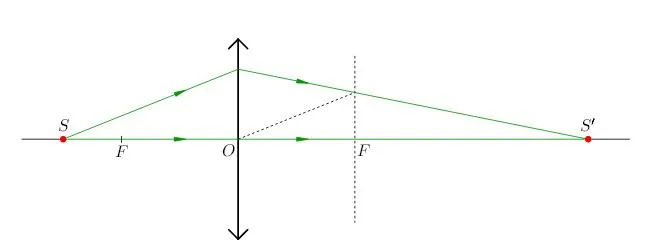
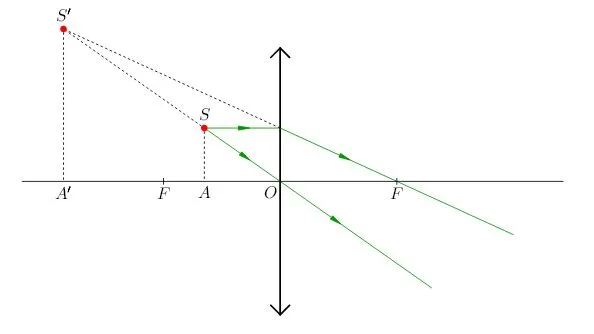
Давайте усложним проблему. Предположим, что точечный источник света расположен на главной оптической оси линзы. Давайте найдем, где формируется образ:
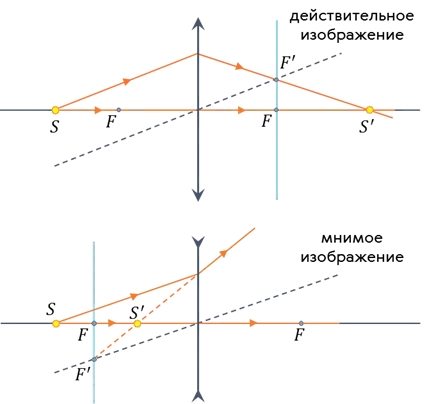
Изображение в собирающей линзе реальное, так как формируется на пересечении самих преломленных лучей, а в рассеивающей линзе — мнимое, так как формируется на пересечении продолжений преломленных лучей.
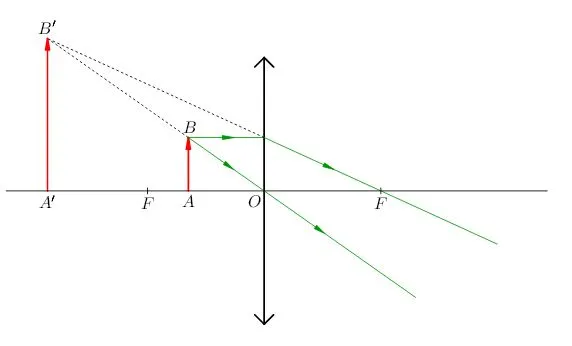
Теперь рассмотрим, как формируются изображения протяженных объектов на разных расстояниях от собирающей линзы.
Во-первых, рассмотрите объект съемки за объективом с двойным фокусом.
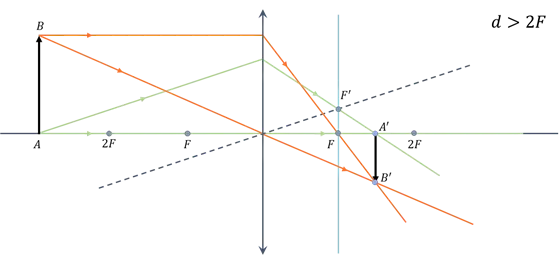
Охарактеризуем полученное изображение. Во-первых, она реальна, так как получается при пересечении преломленных лучей. Во-вторых, она перевернута. И в-третьих, она уменьшена, о чем свидетельствует структура.
Обратите внимание, что если объект перпендикулярен главной зрительной оси, его изображение также будет перпендикулярно ей. Зная это, вы можете создать изображение точки B и отбросить его перпендикулярно главной оптической оси. Это делается следующим образом.
Аналогичным образом можно создавать и характеризовать изображения объектов, находящихся на других расстояниях от объектива.
Объект находится во втором фокусе объектива.
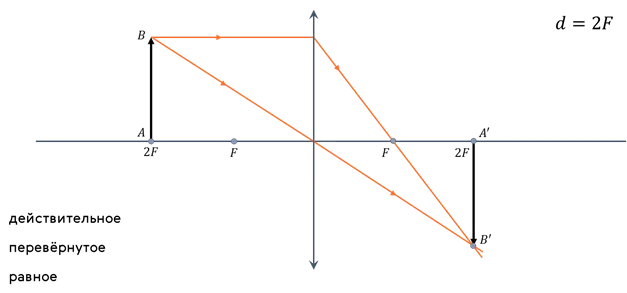
Объект находится между первым и вторым фокусами линзы.
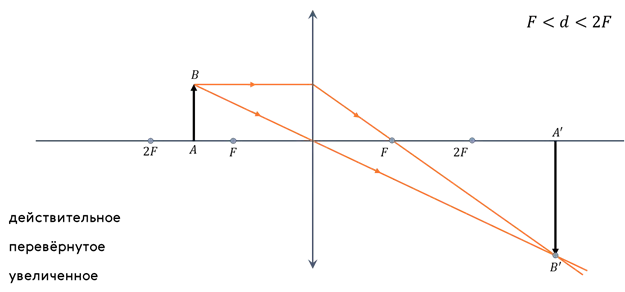
Например, на киноэкране изображение такого типа. Он увеличен — экран намного больше, чем пленка, на которой был записан фильм. Изображения на экране действительно светятся. Чтобы пленка не оказалась перевернутой, потому что изображение на ней перевернуто, проектор также оснащен системой линз, каждая из которых помогает изменить направление световых лучей.








