Наименьший период t, в течение которого движение тела полностью повторяется, называется периодом колебаний. Зная это, можно вычислить частоту колебаний, равную количеству колебаний в единицу времени. Эти величины связаны друг с другом выражением
КОЛЕБАНИЯ И ВОЛНЫ
Механические колебания — это периодически повторяющиеся изменения положения тела (материала) по отношению к положению равновесия. Ширина — максимальное отклонение тела от положения равновесия. Продолжительность — время, необходимое для выполнения полного движения. Вторая единица измерения. Частота — количество колебаний в единицу времени. Частота измеряется в герцах (Гц) — это количество колебаний в секунду. Например, цена 50 Гц означает, что система совершает 50 колебаний в секунду.
Поскольку период — это время, необходимое для совершения полного колебания, частота может быть выражена как
Гармонические колебания — это колебания, которые происходят в соответствии с законом синусов или универсума (гармонический закон).
Фаза колебания () является аргументом периодической функции, описывающей колебание или волновой процесс. Начальная фаза колебания — значение фазы колебания в первый момент времени, т.е. t = 0. Круговая частота является собственной величиной фазы и представляет собой метраж вращения или частоту колебательного движения. Единицы измерения — радиусы в секунду (рад/с).
Это можно записать так
Свободная вибрация — это вибрация, которая возникает из-за того, что внутренние силы системы выходят из равновесия. Собственная частота — это частота свободных колебаний колебательной системы. Амортизационные колебания являются результатом действия кинетических сил (силы трения, аэродинамические силы…). Собственная частота — это частота свободных колебаний колебательной системы. Вынужденная вибрация — это вибрация, возникающая в результате изменения внешних магазинов сил. Координация — это быстрое увеличение ширины колебания, когда частота колебательной системы совпадает с частотой движущей силы.
Математический маятник
Математический маятник — это механическая колебательная система, материальная точка, висящая на нерастяжимой буржуазной нити в поле гравитации. Тип предохранителя, определяющий период колебаний математического маятника. L — длина маятника.
Математика Круговая частота колебаний маятника.
Пружинный маятник
Пружина маятника — это механическая колебательная система, представляющая собой жесткую пружину с материальной точкой массы на одном конце пружины.
Электромагнитные колебания — это периодические изменения интенсивности и магнитной индукции. Колебательный контур — это электрическая цепь, состоящая из емкостного конденсатора и самовозбуждающейся катушки. В цепи наблюдаются свободные электромагнитные колебания. Круговая частота и период собственных колебаний контура определяются по типу Томсона.
Значение ширины (максимума) тока в цепи по отношению к нагрузке конденсатора:.
 Условия возникновения свободных колебаний
Условия возникновения свободных колебаний
Для того чтобы система демонстрировала свободные колебания, должны быть выполнены следующие условия.
- в системе должно быть одно положение равновесия;
- система должна быть выведена из положения равновесия;
- в системе должна возникать сила, возвращающая систему в положение равновесия;
- потери энергии в системе должны быть малы.
В качестве примера можно рассмотреть отложенную пружину. Все эти условия выполняются в

Рисунок 2. положительная пружина.
Обратите внимание, что сила, стремящаяся вернуть маятник в равновесное положение, зависит от неоплачиваемого маятника и от того, насколько велик обход. Поэтому ускорение отложенной массы под действием пружины также направлено в сторону положения равновесия и зависит от обхода. Ускорение — это вторая производная от перемещения. Единственная функция, для которой вторая производная пропорциональна самой функции, — это круговая функция (синус или косинус). Колебания, происходящие по законам круговых функций, называются гармоническими. Такие колебания относятся к колебаниям отложенной пружины. Их типы следующие.
- $x$ – перемещение маятника в момент $t$;
- $A$ – амплитуда колебаний маятника;
- $k$ – жесткость пружины маятника;
- $m$ – масса маятника;
Период свободных колебаний
Период колебаний — это время, в течение которого происходят колебания. Поскольку колебание маятника описывается круговой функцией, его длительность равна длительности этой функции.
Это означает, что зная жесткость пружины и массу отложенного груза, можно определить период.
Период колебаний также может быть измерен немедленно. Измерение периода колебаний $ n $ $ n $ $ t $ дает причину этих размеров, а также период свободных колебаний.
Зная период колебаний маятника и его массу, можно определить жесткость пружины.
Используя период колебаний маятника в ожидании периода колебаний нормальной нити, вы можете найти ускорение свободного падения $ \ mathrm $. Вид периода свободных колебаний маятника с нитью аналогичен виду колебаний пружинного маятника. :.
Необходимо учитывать ограничения типа — максимальная деформация нити во время удержания должна быть намного меньше ее длины.
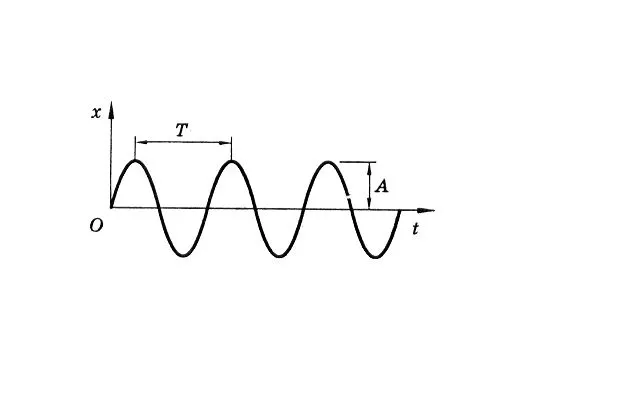
Рисунок 3: Графическое представление колебаний маятника.
Этап 6: Деятельность учителя по рефлексии: закрытие декларативной деятельности ученика: работа по карточкам: «+» означает знание «математического хулиганства». — При работе с каждым возникают вопросы и хочется узнать больше «V» — уметь использовать тип в предмете.
Презентация по физике на тему «От чего зависит период колебания маятников?»
Отметим, что в соответствии с Федеральным законом «Об образовании в Российской Федерации» 273-ФЗ в организациях, осуществляющих образовательную деятельность, обучение и воспитание обучающихся с ограниченными возможностями здоровья организуется в отдельных классах или группах с другими обучающимися.


Уроки профессионального развития
Рабочие листы и материалы для учителей и
2 500+ учебных ресурсов для школьного и домашнего обучения

ОГЭ В проф. ОГС Т.Ю. Дадакина 14.12.2013 Урок физики «От чего зависит период колебаний?»

Краткое содержание курса Курс является частью системы курсов раздела «Механические колебания и волны» в 9 классе и входит в обязательную общеобразовательную программу по физике в вечерней школе. Для повышения эффективности обучения большое внимание уделялось развитию познавательного интереса учащихся. На разных этапах курса формы и методы обучения выбираются на основе психовозрастных особенностей учащихся для решения поставленной цели. На этапе закрепления знаний решаются различные качественные и количественные задачи. Задания подобраны на разных уровнях, с учетом индивидуальных особенностей учащихся. На уроке были использованы элементы технологии развития критического мышления. Я использовала метод группировки знаний учащихся, что позволило представить информацию графически (как пучок) и представить информацию в целостном виде. Метод врезки (показ табличек) использовался во время рефлексии для экономии времени и визуализации продуктивности урока, а также для включения каждого ученика в оценку своей работы. Урок включал как самостоятельную, так и групповую работу, что помогало детям с низкой успеваемостью активно участвовать в работе группы.

Цели урока: Учителя: Закрепить знания по предыдущим темам; Рассмотреть понятие математического и пружинного маятника, уметь определять период колебаний этих маятников и знать их практическое применение; Научить применять на практике знания, полученные на уроке физики. Инструкция: Формирование интереса к предмету, учебе- Формирование инициативы, творческого отношения в учебной деятельности- Содействие развитию нравственных качеств учащихся, ответственности за результаты труда. Развитие: Развитие логического мышления учащихся, их творческих способностей; Развитие способности самостоятельно формулировать выводы; Расширение познавательного интереса; Развитие речевых навыков.

Цели курса: Учителя: Сформировать представление о том, что такое маятники, от чего зависит период колебаний маятников и где можно применить знания законов маятника на практике; Способствовать развитию практических умений и навыков обращения с физическими приборами; Учить выделять главную информацию, сравнивать, развивать умения обобщения, систематизации полученных знаний. Образовательный. Развитие: Развитие у учащихся ожидания познавательной деятельности Развитие навыков нестандартного подхода к решению самых разнообразных проблем, навыков планирования и контроля действий, навыков оценки результатов действий; Развитие навыков умственной деятельности (обобщение, анализ, синтез, сравнение) Включая метапрограммы: Развитие навыков высказывания мнения, выслушивания мнения других Развитие умения работать с понятиями Развитие логического мышления учащихся (обобщение, анализ, синтез, сравнение)
Период колебаний также может быть измерен немедленно. Измерение периода колебаний $ n $ $ n $ $ t $ дает причину этих размеров, а также период свободных колебаний.
Зависимость частоты и периода свободных колебаний от свойств системы
Первоначально мы предположили, что ω 0 — это константа, характеризующая свойства системы:
Здесь периодическая частота связана с периодом и частотой колебаний. Поэтому период и частота колебаний также зависят от характеристик системы.
ω0 = √км. = 2πT. =2πν
Таким образом, период и частота колебаний равны соответственно.
Напомним, что характеристики колебательной системы математического маятника определяются постоянной величиной gl.. Следовательно, период-частота становится равным
Таким образом, период и частота колебаний математического маятника соответственно равны.
Эта формула впервые появилась и была экспериментально проверена голландским ученым Х. Гюйгенсом, современником И. Ньютона.
С увеличением длины маятника увеличивается период колебаний. Она не зависит от массы маятника. Это легко подтверждается экспериментами с различными маятниками. Зависимость периода от гравитационного ускорения также легко распознается. Чем меньше значение g, тем больше период колебаний маятника и, следовательно, тем медленнее идут часы маятника. Так, при подъеме из подвала последнего этажа Московского государственного университета на высоту 200 метров маятниковые часы в виде гири отстают примерно на 3 секунды в сутки. И это только потому, что ускорение свободного падения уменьшается с высотой.
Зависимость периода колебаний маятника от величины g используется на практике. Измерив период колебаний, можно легко определить g. Гравитационное ускорение зависит от широты. Она также изменяется на определенных широтах, поскольку плотность земной коры неоднородна. В местах, где породы плотно упакованы, ускорение силы тяжести больше.
Пример 1. сколько раз колеблется математический маятник длиной 4,9 м за 5 минут?
Число колебаний равно отношению времени к периоду колебаний.
Период колебаний математического маятника определяется следующим уравнением.
N = t2π. √gl. = 300 2-3, 14. √9, 8 4, 9. ≈ 68.
Фаза колебаний
Учитывая амплитуду гармонического колебания, координаты колеблющегося тела в любой момент времени однозначно определяются аргументом синуса или синусоиды, который равен ω0t. Обозначим его через ϕ и получим ϕ
Значение ϕ под знаком косинуса или синуса называется фазой колебания, описываемого этой функцией. Она выражается в радиусе (рад).
Фаза определяет значение регулируемой, а также других натуральных величин (скорости и ускорения, которые также изменяются по гармоническим законам). Из этого можно сделать вывод, что фаза определяет условия колебательной системы в любой момент времени с определенной шириной.
Колебания одинаковой частоты и амплитуды могут отличаться друг от друга по фазе. Поскольку ω0 = 2πT. фаза определяется следующим уравнением
tT. -Соотношение. Количество времени, прошедшего с момента начала осцилляции. Каждому моменту времени, выраженному в виде доли периода, соответствует значение фазы, выраженное в виде радиуса. Например:.
Зависимость координат точек колебаний можно записать не во времени, а в фазе. В этом случае график также будет косинусом (или синусом), но аргументом функции будет не время (период), а фаза, представленная радиусом (см. диаграмму).

Синус отличается от синуса только смещением аргумента π2. (см. схему ниже). Следовательно, для описания гармонических колебаний можно использовать оба закона — синусоидальный и синусоидальный.

Выбор закона зависит от конкретных условий. Если колебание начинается с выведения тела из положения равновесия и его отталкивания, то удобнее использовать закон пришельцев. Потому что в начальный момент времени закон подчинения указывает на то, что организм отклоняется в сторону максимума, вместо того чтобы уравновешиваться. Если вибрация инициирует рывок, то удобнее использовать закон синусов, поскольку начальный момент времени полузакона соответствует положению равновесия.
Колебания, совершаемые по закону синусов и закону синагог, отличаются только фазой, которая сдвигается на одно значение, равное π2.. . Эта величина называется сдвигом или разностью фаз. Таким образом, космотонная функция может быть записана как.
x = x m a x cos. ω0t= x m a x sin. (ω0T +π2…)
Превращение энергии при гармонических колебаниях
Для иллюстрации преобразования энергии в гармонических колебаниях предположим, что силами трения пренебрегаем. Для объяснения смотрите схему ниже.

Положение равновесия шарика соответствует точке геометрии. Если мяч возвращается на расстояние xМакс. и равна ширине, пружина получает потенциальную энергию, которая принимает максимальное значение, равное этому положению.
Когда мяч отпускается, возникает сила упругости, которая направляет мяч влево. По мере уменьшения расстояния между максимальным обходом и положением равновесия потенциальная энергия уменьшается. В то же время, однако, кинетическая энергия шарика увеличивается. Когда мяч впервые выходит из положения равновесия, его динамическая энергия равна нулю, а кинетическая энергия максимальна (и его скорость также максимальна): мяч находится в состоянии максимальной потенциальной энергии.
После точки o расстояние между сферой и положением равновесия снова увеличивается, и потенциальная энергия возрастает. При этом кинетическая энергия уменьшается. А в крайнем левом положении она равна нулю, и потенциальная энергия снова имеет максимальное значение.
Договорившись игнорировать трение, эту колебательную систему можно считать изолированной. В этом случае должен выполняться закон сохранения энергии. Согласно этому закону, полная механическая энергия системы составляет
w = w p + w k = k x 2 x 2.. + m v 2 x 2. = k x 2 m a x 2. = m v 2 m a x 2. = k x 2 m a x 2. = m v 2 m a x 2.
Фактически, из-за сил трения в колебательной системе свободные колебания постоянно амортизируются. Часть механической энергии затем рассеивается в виде тепла. Пример графического представления амортизированных колебаний показан ниже.
Пример нет. 2. груз, прикрепленный к пружине, колеблется в гладком горизонтальном стержне. Найдите отношение кинетической энергии груза к потенциальной энергии системы, когда груз находится в центре между крайним и уравновешенным положениями.
Поскольку груз находится в центре между крайним и уравновешенным положениями, его координаты равны половине ширины.
Теперь потенциальная энергия груза равна
w p = k x 2 2. = k(x m a x 2 …) 2 2. = k x 2 m a x 8.
Согласно закону сохранения энергии, в данный момент кинетическая энергия равна:.
Полная механическая энергия системы равна максимальной потенциальной энергии.
w = w p m a x = k x 2 m a x 2.
Тогда кинетическая энергия
w k = k x 2 m a x 2. -k x 2 m a x 8.
Поэтому причина, по которой кинетическая энергия является потенциальной, заключается в следующем.
Вт кВт-ч. = k x 2 m ax2. -k x 2 m ax8. = k x 2 m ax2. k x 2 m ax8. -k x 2 m ax8. = k x 2 m ax2. 8 k x 2 max. —1 = 4-1 = 3








