Как правило, не всегда легко определить период отдельных колебаний маятника, так как он постоянно находится в движении. Однако, поскольку все колебания маятника одинаковы, для определения периода колебаний можно провести расчеты нескольких колебаний.
Механические колебания.
Проблемы с датчиками ЕГЭ: гармоническая вибрация — амплитуда, период, частота, фаза вибрации — свободная вибрация, вынужденная вибрация, настройка.
Вибрация — это изменение состояния системы, повторяющееся с течением времени. Понятие вибрации охватывает очень широкий спектр явлений.
Вибрация или механические колебания механической системы — это механическое движение тела или системы тел, которое повторяется во времени и происходит вблизи положения равновесия. Равновесное положение — это состояние системы, в котором она может находиться столько времени, сколько необходимо, без внешних воздействий.
Например, когда маятник отклоняют и отпускают, он начинает колебаться. Положение равновесия — это положение маятника, когда он не отклоняется. Маятник может оставаться в этом положении в любое время, пока его не трогают. Когда маятник колеблется, он часто находится вне равновесия.
Сразу же после отпускания отклоненного маятника маятник начинает двигаться, проходит через положение равновесия, достигает противоположного крайнего положения, останавливается в нем, движется в обратном направлении и снова возвращается через положение равновесия. Произошла полная осцилляция. Кроме того, этот процесс периодически повторяется.
Амплитуда колебаний объекта — это величина максимального отклонения от положения равновесия.
Период колебаний — это продолжительность полного колебания. Можно сказать, что за определенный период тело проходит через четыре пути, идущих друг за другом.
Частота колебаний равна обратной величине периода:. Частота измеряется в герцах (Гц) и указывает на количество полных колебаний, происходящих за одну секунду.
Гармонические колебания.
Можно считать, что положение вибрирующего объекта определяется одной координатой. Положение равновесия обозначается через. Основная инженерная задача в этом случае — найти функцию, которая дает координаты тела в любой заданный момент времени.
Естественно использовать периодические функции для математического описания колебаний. Существует множество таких функций, две из которых наиболее важны: полутон и синус. Они обладают многими замечательными свойствами и тесно связаны с широким спектром природных явлений.
Функции синуса и косинуса могут быть получены друг из друга путем сдвига аргументов в противоположные стороны, поэтому вы можете ограничиться одной или другой. Определенно используйте косинус.
Гармонические колебания — это колебания, координаты которых зависят от времени по гармоническим законам.
Давайте рассмотрим важность величин, входящих в это уравнение.
Положительное значение — это максимальное значение модуля координат (поскольку максимальное значение модуля косинуса в единицах), т.е. максимальное отклонение от положения равновесия. Следовательно, это амплитуда колебаний.
Аргумент синусоидальной волны называется фазой колебания. Его значение, которое равно значению фазы тела, называется начальной фазой. Начальная фаза соответствует начальным координатам тела.
Это значение называется частотой его периода. Найдите зависимость между периодом и частотой колебаний. Каждое полное колебание соответствует увеличению фазы в радианах.
Периодическая частота измеряется в радианах в секунду (радиан/сек).
Согласно уравнениям (2) и (3), гармонический закон (1) имеет еще две формы.
График функции (1), представляющей зависимость времени, настроенного на гармонические колебания, показан на рисунке 1.
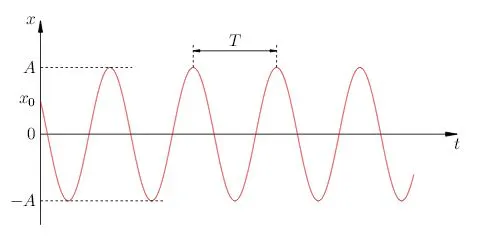 |
| Рис. 1. График гармонических колебаний |
Гармонический закон вида (1) имеет более общий характер. Например, это соответствует ситуации, когда один маятник одновременно подвергается двум начальным воздействиям, обходится одним размером и получает начальную скорость. Есть два важных особых случая, когда одно из этих действий не было выполнено.
Мы пытаемся отклонить маятник, но начальная скорость не была задана (он отпускается без начальной скорости). В этом случае ясно, что мы можем поставить. Мы принимаем коварный закон:.
График гармонического колебания в этом случае показан на рисунке 2.
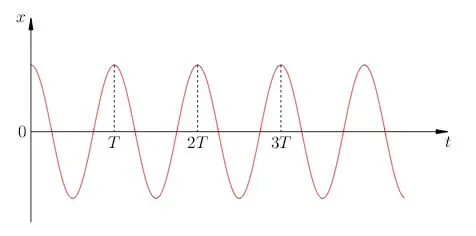 |
| Рис. 2. Закон косинуса |
Предположим, что маятник не отклоняется, а получает начальную скорость из положения равновесия от удара. В этом случае его можно носить. Возьмем закон знаков:.
График колебаний показан на рис. 3.
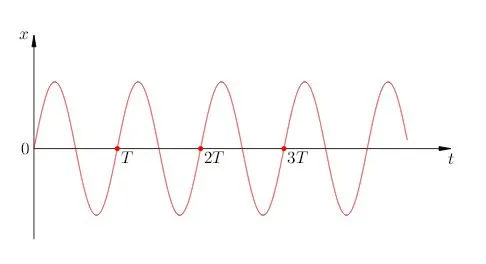 |
| Рис. 3. Закон синуса |
Уравнение гармонических колебаний.
Вернемся к общему закону гармонии (1). Давайте разграничим это равенство.
Далее, различают равенство исходов (4):.
Сравните уравнение (1) относительно координат и уравнение (5) относительно ускорения. Мы видим, что проекция ускорения отличается только от одной факторной координаты.
Эта зависимость называется уравнением гармонического колебания. Его также можно переписать в таком виде.
С точки зрения математики, уравнение (7) является дифференциальным уравнением. Решением дифференциального уравнения является функция (а не число, как в обычной алгебре). Таким образом, можно доказать, что:.
— Слагаемые уравнения (7) являются произвольными функциями произвольной формы (1).
— Другая функция не является решением уравнения.
Другими словами, соотношения (6) и (7) описывают гармонические колебания только с круговыми частотами. Эти две константы определяются начальными условиями, начальными значениями координат и скорости.
Звуковые волны — это упругие волны, которые вызывают ощущение звука у человека и представляют собой зоны сжатия и разбавления, передающиеся в течение длительного времени.
Период колебаний
Вибрации — это движения или процессы, которые повторяются в течение определенного периода времени.
Система, осуществляющая вибрацию, называется колебательной системой или осциллятором.
В зависимости от природы, процесс вибрации может быть механическим, электромагнитным и т.д.
Внимание. Если врач обнаружит, что у вас есть проблема, которая вас беспокоит, у вас может быть серьезная проблема (даже выкидыш). Если вы не можете написать свой собственный, вы можете заказать его здесь.
Свободные или естественные вибрации — это вибрации, наблюдаемые в системе, предоставленной самой себе после нарушения равновесия.
Вынужденные колебания — это колебания под воздействием внешних сил, которые регулярно меняются.
Механическая вибрация относится к категории принудительной вибрации.
Гармонизированные вибрации — это вибрации, определяемые естественными размерами, которые изменяются в соответствии со знаком или косметическим законом.
Различные периодические процессы, повторяющиеся через равные промежутки времени, могут быть записаны как суммы или суперфронты гармонических колебаний.
Определение периода колебаний, формула
Колебательные процессы могут быть выражены в виде уравнения. Гармонические колебания цены X могут быть выражены в следующем виде
\(x(t))= a \ times \ cos \ left (\ omega _t+\ phi _ \ right)\)
где ⌘(x(t)⌘) — отклонение натуральной величины качелей от равновесного значения.
A представляет собой ширину гармонического колебания.
\(ߡ омега _ \ справа) — круговая или кольцевая частота колебаний.
\(Lo_CP_t) = (co_t + cp _)\) — это начальная фаза характеристического колебания в момент времени t = 0, которая может быть определена путем выбора начальной точки.
\(cp(t) = (co_t + cp _)\) — это фаза колебания в момент времени t, определяемая радиусом и соответствующая значению количества колебаний в конкретный момент времени.
Для материальной точки массой m характеристика x соответствует смещению объекта из положения равновесия. Обратите внимание, что амплитуда и частота гармонических колебаний являются постоянными величинами. Исходя из того, что cos изменяет значение в диапазоне от +1 до -1, параметр x изменяется от +A до -A. С тех пор:.
\ cos \ слева (⌘ альфа +2 \ pi \ справа) = \ cos \ альфа, ⌘)
В этом случае x остается неизменным, а фаза колебаний увеличивается на $ 2 \pi$.
Период колебаний T — это минимальное время возвращения колебательной системы в исходное состояние, которое определяется произвольно.
В этом случае фаза увеличивается на \(2 \ pi:ߡ).
\(섹 омега _(t + T) + \ фи _ = \ слева (섹 омега _t + \ фи _ \ справа) + 2 \ пи \).
Из этого уравнения можно рассчитать период колебаний.
Частота колебаний v является обратной величиной периода колебаний. Это количество полных колебаний, совершаемых в единицу времени.
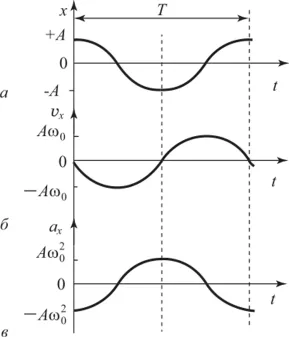
График показывает гармоническое колебание. где α — зависимость перемещения x от времени /, β — зависимость скорости vx от времени C и γ — зависимость ускорения ax от времени t.
Единицей частоты в СИ является герц (Гц). Это частота периодического цикла полных колебаний, происходящих за одну секунду.
Можно представить, что материальная точка совершает линейное гармоническое колебание вокруг оси x вокруг положения равновесия, которое является начальной точкой координат. Движение частиц носит колебательный характер и характеризуется скоростью и ускорением. Особенности этого процесса можно описать следующим образом.
Shift \ (x = A \ times \ cos \ left (⌘ omega _t + \ phi _ \ right) ⌘)
Скорость 섹 (v _ = \ точка = -A \ omega _ \ times \ sin \ left (섹 omega _ t + \ phi_ \ right) = A \ omega _ \ times \ cos \ left (섹 omega _ t + \ phi_ + \ frac<\pi >\ направо) \ направо)
\ a _ = \ точка
Как найти период для физического маятника
При малых углах отклонения 섹 (⌘ varphi \) естественный маятник совершает гармонические колебания. Его вес можно рассматривать как добавление к центру тяжести в точке C. Сила, которая возвращает маятник в положение равновесия, — это сила F, которая является компонентом силы тяжести.
Отрицательные значения в правой части уравнения означают, что сила F направлена в сторону уменьшения угла ⌘ (⌘ альфа \).
Для меньших углов ⌘ (⌘ varphi \) уравнение можно записать в следующем виде
Примеры решений
Шарик на нити колеблется 60 раз за 2 минуты. Найдите период и частоту колебаний шарика.
ОТВЕТ: период колебаний маятника равен 2 с, а частота — 0,5 Гц.
По графику зависимости координат от представленного времени необходимо рассчитать характеристики колебательного движения тела.
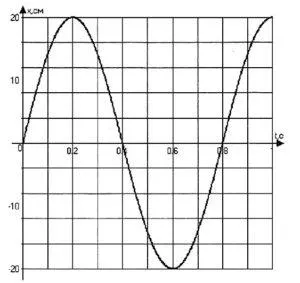
\x(t) = A \ sin 2 \ pi Vt = 0,2 \ sin 2 \ pi \ раз 1,25t = 0,2 \ sin 2,5 \ pi t \)
ОТВЕТ: амплитуда колебаний маятника равна 0,2 м, период колебаний 0,8 с, частота колебаний 1,25 Гц, а выражение для координат записано в следующем виде\(x(t) = 0,2 \ sin 2,5 \ pi t \)
Определите длину математического маятника, гармонично колеблющегося с частотой 0,5 Гц на поверхности Луны. В этом случае ускорение свободного падения составляет 1,6 м/с2.
Период колебаний математического маятника рассчитывается по следующему уравнению
Чтобы выразить длину маятника, обе части уравнения нужно возвести в квадрат.
Математический маятник — это точка массы, подвешенная на невесомой, нерастяжимой нити, прикрепленной к подвесу и помещенной в гравитационное поле.
Колебательный процесс
Одним из наиболее распространенных процессов в природе являются колебания. Процесс вибрации обычно заключается в изменении значений параметров рассматриваемой системы, которые регулярно перемещаются вперед и назад за определенное положение равновесия.

Рисунок 1. Вибрационные процессы в природе.
Колебания маятника
Простейшим примером колебательного процесса является маятник, который представляет собой легкую нить с грузом на конце. Его перемещают из положения равновесия в крайнее положение, а затем отпускают (отклонение должно быть намного меньше длины струны, чтобы уменьшить влияние трения).
Вес начинает двигаться в сторону противоположного крайнего значения. Здесь его скорость падает до нуля, и он колеблется в обратном направлении к исходному положению. (На самом деле маятник имеет потери на трение и немного отстает от начальной точки, но это небольшое отклонение пренебрежимо мало).
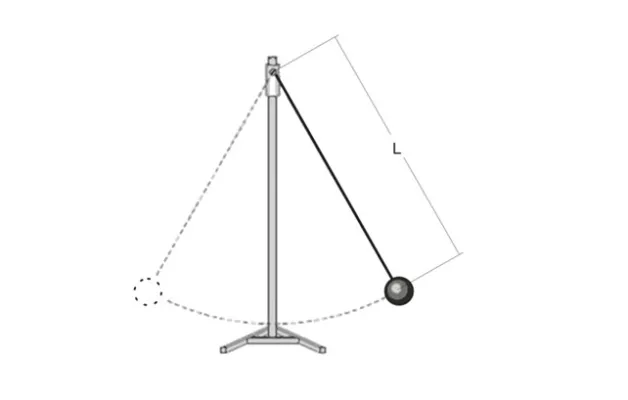
Рисунок 2. Колебания маятника.
Полное движение, начинающееся от начальной точки и продолжающееся до ближайшего возвращения к ней, называется колебанием.
Период колебаний
Сравнивая несколько последовательных колебаний, можно увидеть, что они очень похожи. При этом каждое колебание длится одинаковое время.
Время, необходимое для возникновения простого колебания, называется периодом колебания. Он обозначается заглавной латинской буквой $T$.
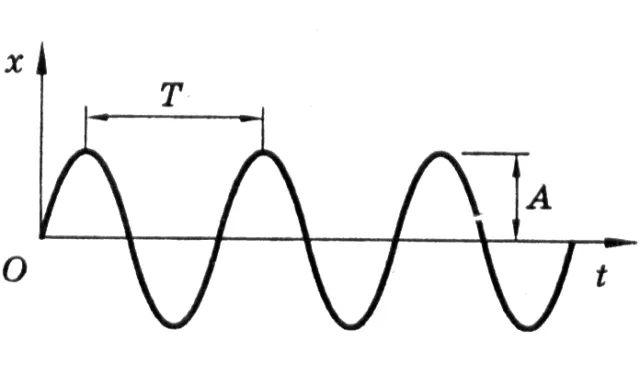
Рисунок 3: Период колебаний на графике.
Напомним, что в системе СИ время измеряется в секундах. Если период слишком мал, берутся дробные единицы миллисекунд (мс, $ 10 ^ $ секунд), микросекунд (мкс, $ 10 ^ $ секунд) и наносекунд (нс, $ 10 ^ $ секунд).
Как правило, не всегда легко определить период отдельных колебаний маятника, так как он постоянно находится в движении. Однако, поскольку все колебания маятника одинаковы, для определения периода колебаний можно провести расчеты нескольких колебаний.
Формула для периода колебаний выглядит следующим образом
Можно быстро различить периоды колебаний от 50 микросекунд (самый громкий) до десятилетий (например, 12 лет — один год для Юпитера). С помощью как экономики, так и технологии можно испытать периоды колебаний от $ 10 ($ нс (период рентгеновских лучей) до 250 миллионов лет (время вращения Солнечной системы вокруг центра нашей галактики).
Пружинный маятник — это груз, прикрепленный к пружине, который может колебаться как горизонтально, так и вертикально.
Частота колебаний — это количество полных колебаний в единицу времени. Символ обозначается в ᢙ (ᢙ ню \), а единица времени — с -1 или Гц (Герц).
1 Гц — это частота колебательного движения, при котором одно полное колебание происходит в секунду.
Период и частота колебаний взаимно обратны.
Частота периода — это число колебаний за 2π секунды. Название ᢙ (ᢙ омега \) и единица измерения — рад/с.
Свободные колебания (математический и пружинный маятники)
Свободные колебания — это колебания, совершаемые объектом под действием внутренних сил системы за счет первоначального запаса энергии после удаления от постоянного положения равновесия.
Условия, при которых возникает свободная вибрация:.
- при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
- силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.
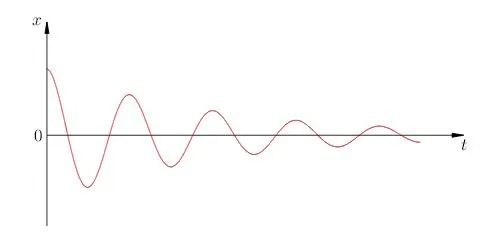
В присутствии сил трения свободная вибрация обесценивается. Амортизация — это колебание, ширина которого уменьшается со временем.
Математический маятник — это материальная точка, парящая над голой ненатянутой струной.
Период колебаний математического маятника:.
Частота колебаний математического маятника:.
Круговая частота колебаний математического маятника:.
Максимальная скорость колебаний математического маятника:.
Максимальное значение ускорения колебаний математического маятника:.
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением.
Период свободных колебаний математического маятника, движущегося вверх с ускорением или замедлением:.
Периоды свободных колебаний математического маятника, движущегося горизонтально с ускорением или замедлением:.
Мгновенное значение динамической энергии математического маятника, поднимающегося в процессе колебаний на высоту, ⌘(h \), определяется по формуле
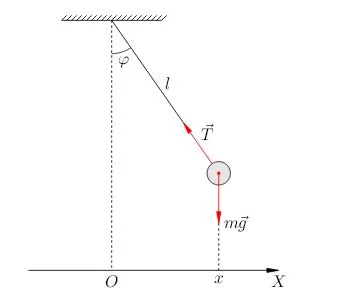
где Į(l \) — длина струны, а Į(Į альфа \) — угол отклонения от вертикали.
Пружина на удержании — это тело, подвешенное на пружине и колеблющееся вдоль вертикальной или горизонтальной оси под действием упругости пружины.

Длительность колебания пружины:.
Частотная вибрация пружины при удержании:.
Частота круговых колебаний пружины на удержании:.
Максимальная скорость колебаний пружины при удержании:.
Максимальное ускорение качающейся пружины при удержании:.
Мгновенная динамическая энергия пружины, находящейся в состоянии покоя, может быть найдена по типу.

Ширина динамической энергии — это максимальное значение динамической энергии, до синуса или косинуса.
Важно! Если маятник является пружиной, но нет математического маятника (естественного маятника), то круговая частота, период и частота колебаний не могут быть рассчитаны по типу, применяемому к математической и ожидающей пружине. В этом случае эти размеры рассчитываются в зависимости от типа силы или действия, приложенного к маятнику.
Резонанс
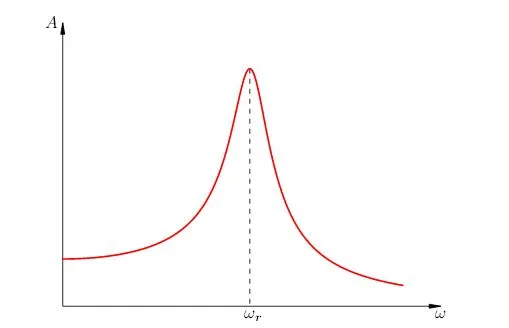
Регулировка — это явление внезапного увеличения ширины колебаний, которое происходит при совпадении частоты налагаемой силы и частоты колеблющегося тела.

\(v_0 \) — собственная частота маятника.
На этой диаграмме показаны кривые координации для среднего значения различных ограничений. Чем ниже трение, тем выше и круче кривая координации.
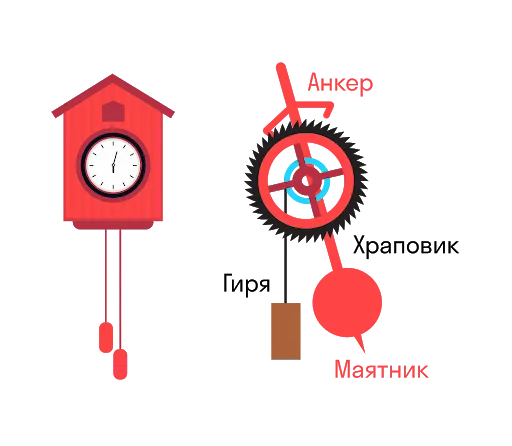
Явление координации учитывается при регулярном изменении нагрузок на машины и различные конструкции. Координата также используется в акустике, радиальной динамике и т.д.








