Тело переместилось из точки А в точку Б. Перемещение тела — это прямая связь между этими точками (размер вектора). Путь, который проходит тело, — это длина траектории. Очевидно, что смещение и маршрут не следует путать. Измерения вектора перемещения и длины маршрута совпадают только в случае прямолинейного движения.
Формулы для расчета линейной скорости
Скорость равномерного движения тела является натуральной величиной и определяет путь, который проходит тело за единицу времени.
В Международной системе единиц (СИ) единица линейной скорости является производной от двух основных единиц.
В Международной системе СИ скорость измеряется в метрах в секунду (м/с). Единицей скорости является скорость равномерного движения, при которой тело перемещается на один метр в секунду. Скорость также может быть измерена.
Внимание. Если преподаватель обнаружит плагиат в вашей работе, серьезных проблем не избежать (вплоть до ликвидации). Если вы не можете написать работу самостоятельно, закажите ее здесь.
Связь между линейной и угловой скоростями
Скорость в точке совершения кругового движения называют линейной скоростью, отделяя это понятие от термина угловая скорость. Во время вращения абсолютно твердое тело имеет разные линейные скорости в разных точках, но значение угловой скорости остается постоянным.
Существует зависимость между линейной скоростью и угловой скоростью тела, вращающегося по кругу. Маршрут для точки радиуса r выглядит следующим образом.
Если предположить, что время вращения тела равно периоду t, то мера линейной скорости вычисляется по следующему виду
Он получает следующее уравнение.
Этот тип указывает на увеличение линейной скорости тела по мере удаления от оси вращения. Например, точка v = 463 м/с движется вдоль экватора Земли, а точка на широте Санкт-Петербурга будет двигаться со скоростью v = 233 м/с. Если точка находится на полюсе планеты, то скорость падает до v = 0.
Мера центрального ускорения точки тела, совершающего равномерное вращательное движение, определяется угловой скоростью тела и радиусом цикла. Уравнение записывается в следующем виде
Так человек преображается:.
Для подведения итогов расчета можно описать все возможные уравнения, применимые для определения центрального ускорения.
Так, рассмотрим простейшую пару движений, характеризующих идеально твердое тело, включая соотношение форообразных и вращательных движений. Однако стоит отметить, что сложные движения, совершаемые идеально твердым телом, могут быть определены суммой двух независимых движений.
Закон независимости движения используется для описания сложных движений абсолютно твердого тела.
Формулы для нахождения линейной скорости
Если скорость характеризуется постоянной величиной, то тело движется равномерно. Вид расчета скорости таких движений имеет следующий вид
где s — расстояние, которое нужно пройти, т.е. длина линии, т.е.
T — время, затрачиваемое телом на прохождение заданного пути.
Линейная скорость V — это натуральная величина расстояния, которое тело пробегает за определенное время.
Основным видом определения линейной скорости является следующее уравнение
t обозначает время прохождения тела по маршруту S.
Другой вариант уравнения имеет вид
t обозначает время прохождения тела через носовую часть L.
В некоторых научных источниках скорость обозначается строчной буквой v. Другим уравнением для расчета линейной скорости является уравнение равенства.
В этом случае 2p представляет собой полный цикл, 360 угловых градусов. Вектор скорости является касательной к траектории движения тела.
Модуль скорости
Арифметическое значение скорости может отличаться в зависимости от выбранной единицы измерения. Помимо численного значения, скорость характеризуется также ее направлением. В физике численное значение скорости называется ее коэффициентом.
Если скорость имеет определенное направление, то она является вектором. Поэтому скорость — это естественный размер вектора. Измерение скорости записывается как v, а вектор скорости как ⌘ (⌘ vec \).
Следует отметить, что такие величины, как маршрут, время и длина, встречаются только в числовых значениях. Они называются фазовыми величинами. Если тело движется неравномерно, справедливо использовать в расчетах средние скорости.
Стоит отметить, что все они имеют интуитивно понятную рабочую среду и содержат все виды таблиц, используемых для решения задач, соответствующие контракты и пояснения к процедурам расчета.
Траектория, радиус-вектор, закон движения тела
Кинематика была изучена еще Аристотелем. Правда, она не называлась кинематикой. Позже Галилео Галилей сыграл большую роль в развитии кинематики, которая изучала технику, особенно свободное падение и бездействие тела.
Таким образом, кинематика решает вопрос: как движется тело? Его не интересуют причины, по которым они переезжают. Кинематику не интересует, едет ли автомобиль сам по себе или его толкает гигантский динозавр. Его это совершенно не интересует.
Далее мы рассмотрим простейшую кинематику — кинематику точек. Представьте, что тело (материальная точка) движется. Неважно, что это за тело, мы все равно думаем о нем как о материальной точке. Это может быть НЛО на небе, а может быть бумажный самолетик из окна. Еще лучше, если это будет новый автомобиль, на котором вы отправитесь в путешествие. Перемещаясь из точки A в точку B, точка описывает воображаемую линию, называемую орбитой. Другое определение колеи — это дорога с радиусом тонких опухолей. То есть, это линия, описываемая концом радиус-вектора точки при ее движении.
Радиус-вектор — это вектор, определяющий положение точки в пространстве.
Чтобы знать положение тела в пространстве в любой момент времени, необходимо знать законы движения тела, то есть зависимость координат (или радиус-вектора одной точки) от времени.
Перемещение и путь
Тело переместилось из точки А в точку Б. Перемещение тела — это прямая связь между этими точками (размер вектора). Путь, который проходит тело, — это длина траектории. Очевидно, что смещение и маршрут не следует путать. Измерения вектора перемещения и длины маршрута совпадают только в случае прямолинейного движения.
В системе СИ перемещение и длина маршрута измеряются в метрах.
Смещение равно разности между исходным радиус-вектором и радиус-вектором в конце времени. Другими словами, это увеличение радиус-вектора.
Скорость и ускорение
Средняя скорость — это натуральная величина вектора, равная отношению вектора смещения ко времени возникновения.
Теперь представьте, что время уменьшается, сжимается и становится достаточно маленьким. Она стремится к нулю. В этом случае мы не можем говорить о средней скорости. Скорость мгновенна. Те, кто помнит основы математического анализа, быстро понимают, что он невозможен без дифференцирования.
Мгновенная скорость — это векторная натуральная величина, равная производной от радиуса вектора по времени. Мгновенная скорость всегда направлена по касательной к орбите.
В системе СИ скорость измеряется в метрах в секунду.
Если тело движется не равномерно и не прямолинейно, возникает ускорение, а также скорость.
Ускорение (или мгновенное ускорение) — это натуральная величина вектора и является второй производной радиального вектора по времени и, следовательно, первой производной мгновенной скорости.
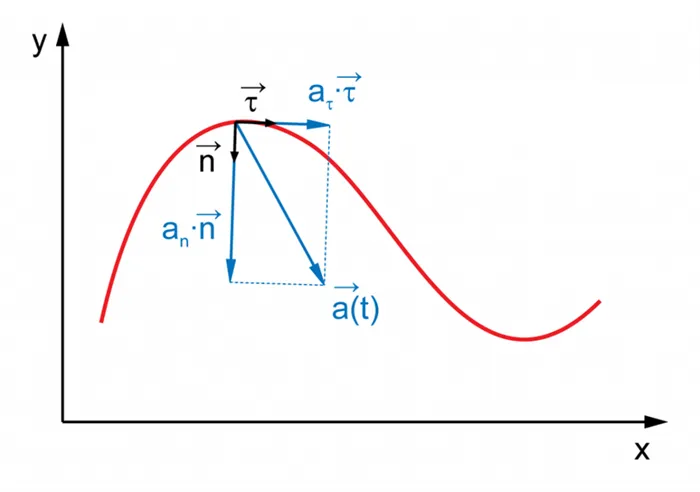
Ускорение показывает, насколько быстро изменяется скорость тела. Для прямолинейных движений адреса скорости и ускорения совпадают со случайностью. Однако для криволинейных движений вектор ускорения может быть проанализирован на две составляющие: тангенциальное ускорение и нормальное ускорение.
Тангенциальное ускорение показывает, насколько быстро изменяется скорость тела и касается траектории.
Нормальное ускорение, с другой стороны, указывает на скорость изменения направленной скорости. Векторы нормального и тангенциального ускорения перпендикулярны друг другу, а вектор нормального ускорения направлен к центру окружности, в которой движется точка.
Здесь r — радиус цикла, в котором движется тело.
Скорость обозначается маленькой латинской буквой V, время движения — строчной буквой t, а расстояние, через которое оно проходит, — маленькой буквой s. Скорость, время и расстояние связаны друг с другом.
Скорость движения
Скорость имеет натуральную величину, равную отношению перемещения к периоду, за который оно происходит.
Скорость — одна из основных характеристик механического движения. Она выражает суть движения. Другими словами, он определяет разницу между недвижимостью и движущимся телом.
Единицей скорости в системе СИ является М/с.
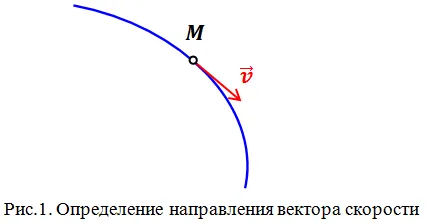
Важно помнить, что скорость — это векторная величина. Направление вектора скорости определяется траекторией движения. Вектор скорости всегда является касательной к траектории в точке прохождения движущегося тела (рис. 1).
Например, рассмотрим колеса движущегося автомобиля. Колесо вращается, и все его части движутся по кругу. Брызги от колеса летят по касательным к этим окружностям и указывают направление вектора скорости.
Таким образом, скорость характеризует направление движения тела (направление вектора скорости) и скорость этого движения (мера скорости).
Отрицательная скорость
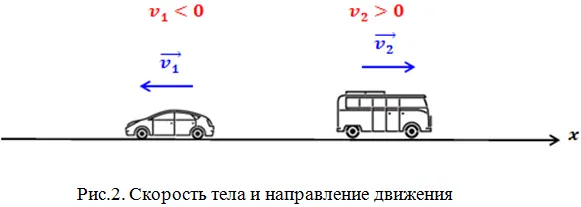
Может ли скорость тела быть отрицательной? Да, возможно. Отрицательная скорость тела означает, что тело движется в направлении, противоположном координатным осям выбранной системы отсчета. На рисунке 2 показано движение автобуса и автомобиля. Скорость автомобиля отрицательна, а скорость автобуса положительна. Помните, что при обозначении скорости имеется в виду проекция вектора скорости на координатные оси.
Примеры решения задач по теме «Скорость»
| Задание | Автомобиль прошел первую половину пути между двумя населенными пунктами со скоростью 90 км/ч, а вторую половину – со скоростью 54 км/ч. Определите среднюю скорость автомобиля. |
| Решение | Было бы неверным вычислять среднюю скорость автомобиля как среднее арифметическое двух указанных скоростей. |
Используйте определение средней скорости.
Векторные символы могут быть опущены, так как они считаются простыми движениями.
Время, необходимое автомобилю для преодоления всего расстояния:.
Где время, необходимое для прохождения первой половины маршрута, а где время, необходимое для прохождения второй половины маршрута.
Общий путь равен расстоянию между населенными пунктами.
Заменив эти проценты в формуле на среднюю скорость, получим

![]()
Если известны скорость и расстояние, можно найти время.
Например, нам нужно пройти 500 метров от нашего дома до спортивного клуба. Мы должны идти туда пешком. Наша скорость составит 100 метров в минуту (100 м/мин). Сколько времени вам требуется, чтобы добраться до спортивного зала?
Если мы проходим 100 метров в минуту, то равняется ли 100 метров за минуту 500 метрам?
Чтобы ответить на этот вопрос, нужно разделить 500 метров на пройденное расстояние, то есть на 100. Затем пришло время добраться до спортивного раздела.
t = s:v = 500:100 = 5 (минуты в спортивном зале)
Вам нравятся уроки? Присоединяйтесь к новой команде Facebook и начните получать уведомления о новых уроках.
Хотите ли вы поддержать проект? Воспользуйтесь кнопкой ниже.
35 thoughts on “Расстояние, скорость, время”
Очень хороший сайт! Добавил его в избранное на долгое время! Спасибо за проект! Очень полезно! На самом деле, незнание математики — это проблема огромного масштаба. Миллионы людей не понимают этого. И мало кто может это хорошо объяснить. Благодаря вам — у людей есть возможность стать лучше 🙂 .
В самих учебниках существует недопонимание относительно таких заданий. Здесь не говорится о том, движутся ли студенты с постоянной скоростью или они изменились. Ответом будет средняя скорость студентов на протяжении всего маршрута ….
Очень простое и понятное объяснение. Просто узнайте тип и замените. Большое спасибо.
Из этого вида можно извлечь уравнение для нахождения конечной скорости точки: v = (v 2 0-2 * a * s)½. Если v0 = 0 в начале, то тип можно упростить в виде: v = (2 * a * s)½.
Движение по окружности
Круговое движение — это простейший случай криволинейного движения, когда тело движется вокруг одной точки. Очень важно отделить круговое движение тела от вращения.
Когда тело вращается, все его точки описывают окружность, расположенную на параллельных уровнях. Центры всех окружностей являются прямыми перпендикулярами к уровню окружности, называемому осью вращения. Оси вращения расположены внутри и снаружи тела.
Круговое движение тела с постоянной по модулю скоростью — это движение, при котором тело за каждый равный промежуток времени проходит равную дугу. Это очень похоже на равномерное движение, только в данном случае мы имеем дело с арками.
При круговых движениях тело движется вокруг одной точки, в то время как при вращательных движениях все части тела движутся вокруг оси вращения.
Центростремительное ускорение
При круговом движении измерение скорости постоянно, но направление скорости постоянно меняется. Центробежное ускорение отвечает за изменение направления скорости.
Центробежное ускорение
ACE — центробежное ускорение М/с 2
Мотоцикл движется по круглому участку дороги радиусом 120 м со скоростью 36 км/ч. Что такое центробежное ускорение на мотоцикле?
Центробежное ускорение тела при использовании данного типа
В рассматриваемом утверждении скорость указана в километрах в час и радиус измерения. Поэтому, чтобы избежать дезинтеграции раствора, скорость необходимо перевести в м/с.
Это заменит цену формулы.
aц = 10 2/120 = 100/120 =10/12≃0,83 м/с 2
ОТВЕТ: центробежное ускорение велосипедиста составляет 0,83 м/с 2








