Высокий крутящий момент двигателя значительно улучшает тяговые характеристики, даже на низких скоростях, благодаря динамике доводки автомобиля. Загрузка машины и функциональность на бездорожье.
Формула момента силы
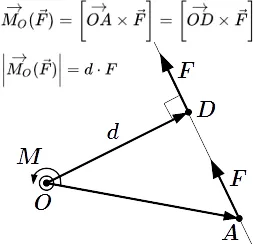
Векторное произведение радиус-вектора ($ \ бар $), спроектированного на точку O (рис. 1), построено относительно точки o ($ \ бар $ \ бар $).
На рисунке 1 вектор ($ \ бар $) и вектор $ \ бар Ray с точкой o силы находятся на уровне геометрии. В этом случае вектор крутящего момента ($ \ бар $) перпендикулярен уровню геометрии и удален от нас. Вектор крутящего момента является осью. Направление вектора силы выбирается таким образом, чтобы вращение вокруг точки направления силы и вектора $ \ bar $ создавало систему по часовой стрелке. Направление импульса и углового ускорения совпадают.
Барный вектор $ \ имеет следующие цены
Где $ \ альфа $ — угол между радиус-вектором и направлением вектора силы.
Момент силы относительно оси
Момент силы оси имеет натуральную величину, равную проекции силы вектора момента до выбранной точки оси на конкретную ось. Выбор точки не является критическим.
Главный момент совокупности сил с точки зрения точки O равен $ \ бар (момент силы), равный сумме моментов всех сил, действующих в той же точке.
Эта точка называется центром тяжести системы сил.
Если есть два основных крутящих момента ($ \ бар $ и $ \ накладка
Где $ \ бар_.
В общем, результат действия любой системы сил, приложенной к твердому телу, совпадает с результатом действия главного момента $ \ bar $ системы сил и главного вектора системы сил, приложенной к центральному телу. Гравитация (точка O).
Основные единицы измерения силы вращения в системе СИ: m = N-M
Задание. На рисунке 1 показано тело с осью o. Является ли движущая сила силы, действующей на тело, относительно этой оси нулевой? Ось и вектор силы находятся на уровне геометрии.
Решение. В качестве основы для решения задачи по определению момента мощности рассмотрим уравнение.
Векторное произведение (как показано на диаграмме) $ \ бар \ neq 0, ⌘ бар \ neq 0 $. Векторное произведение (1.1) не равно нулю, так как угол между вектором сил и вектором радиусов также равен нулю (или $ 180^$). Поэтому импульс силы не равен нулю.
Ответ. $ \ бар \ neq 0 $

Мы уже помогли 4 372 студентам и школьникам сдать работу от решения задач до диссертации! Узнайте стоимость своей работы за 15 минут!
Задание. Угловая скорость вращающегося твердого тела изменяется в соответствии с диаграммой на рисунке 2. В какой точке диаграммы момент силы, действующей на тело, равен нулю?
Решение. Движущая сила, действующая на вращающееся твердое тело, может быть найдена с помощью фундаментальных законов вращательного движения.
Где $ \ varepsilon $ — угловое ускорение вращения тела.
(Пользуясь (2.2) и записывая (2.1), имеем.
$ i \ neq 0 $ (инерционный момент ненулевой), производная угловой скорости должна быть нулевой, чтобы удовлетворить условию m = 0. Производная равна нулю в крайних точках. Крайней точкой на диаграмме является точка 3.
Как видите, это состояние вращательного равновесия похоже на метафорическое состояние равновесия. Условие равновесного вращения удобно использовать для определения момента силы, необходимого для уравновешивания неравномерно вращающегося объекта.
Момент силы: простыми словами и на живых примерах
Крутящий момент — это векторная физическая величина, связанная с вращением, и используется только как одно из свойств вращательного движения.
Ступенчатое значение крутящего момента определяется как произведение силы (радиуса), приложенной к вращающемуся рычагу. Радиус вращения равен расстоянию от центра вращения до точки действия силы.
M = F * R, где F — сила, а R — радиус вращения (плечо).
В Международной системе единиц (СИ) расстояния измеряются в метрах (м), а силы — в ньютонах (Н), поэтому размеры крутящего момента указываются в ньютон-метрах (Н*м). Для облегчения регистрации слишком больших или слишком малых значений крутящего момента часто используются соответствующие приставки «кило», «мега», «миля» и т.д. Например, 1 кН *м равен 1000 Нм, а 1 МН *м равен 1000000 Нм.
В технических текстах могут встречаться старые названия, которые являются функциональными терминами, например, «килограмм электроэнергии», который используется как единица измерения мощности. Этот показатель может быть выражен в кг или кГ, а крутящий момент такой силы измеряется в Н*кг или Н*кг. Реже встречаются единицы измерения мощности в динах, чем в очень старой системе GHS (сантиметры, граммы и секунды). Поэтому единицей измерения крутящего момента для этой системы является дин*см.
Момент крутящий и вращающий
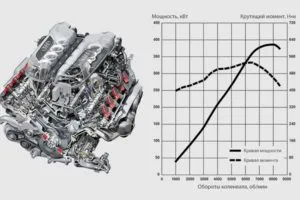
В зависимости от источника крутящий момент имеет два значения.
Оба часто используемых понятия можно рассматривать как синонимы, так как в целом они обозначают одно и то же количество. Однако крутящий момент — это величина, связанная с внешним приложением силы, т.е. с источником силы, и указывается в точке или узле, где прикладывается сила, приводящая механизм в действие. Подумайте об этом в простейшей форме механического взаимодействия, например, о затягивании гайки гаечным ключом. К самому ключу прикладывается сила, которая, в свою очередь, прикладывает крутящий момент к системе. В то же время крутящий момент прикладывается к резьбовой гайке как к движущему элементу механизма.
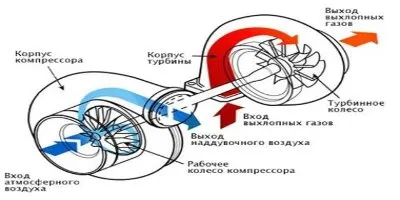
Примеры более сложных механизмов, таких как автомобильный турбокомпрессор, можно найти на сайте https: //centr-turbin.com, чтобы узнать больше о простом крутящем моменте. Турбокомпрессор используется для повышения эффективности и мощности двигателя за счет использования энергии выхлопных газов автомобиля, которая подается на турбину и перемещает вал турбокомпрессора для обеспечения принудительного потока воздуха в камеру сгорания цилиндра двигателя. На этой схеме движение выхлопных газов в турбинной секции показано красным цветом, а движение воздуха в компрессорной секции — синим.
В этом случае крутящий момент передается на механизм под действием выхлопных газов в турбинной секции. В то же время на валу турбокомпрессора создается крутящий момент, который передает вращение на крыльчатку компрессора, и компрессор нагнетает воздух в цилиндры двигателя.
Сила есть — ума не надо?
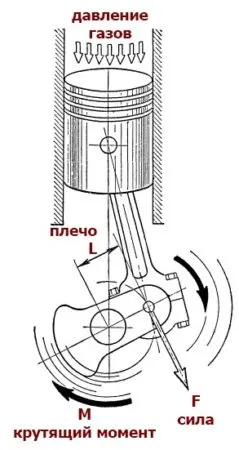
И в самых простых вещах есть нечто большее. Вернемся к тому же незначительному затягиванию гаек. Для затягивания гайки требуется определенный крутящий момент. И это независимо от требуемой силы. На схеме длина рычага ключа составляет 200 мм или 0,2 м. Чтобы захватить конец ключа и затянуть гайку, необходимо передать 100 н * 0,2 м = 20 н * м. Однако, если вы вращаете гайку в середине рукоятки с половиной плеча рукоятки, вам нужно приложить те же 20 н * м, но вдвое больший момент: 200 н * 0,1 м = 0,2 м.
Поэтому на практике для достижения того же эффекта необходимо использовать больший рычаг, чтобы затратить меньшую мощность. Будь то закручивание гаек или вращение тяжелых камней. Это связано с тем, что крутящий момент является естественной величиной, характеризующей вращательные движения. В широком смысле слова, крутящий момент — это само вращение. Вращение состоит из двух элементов: силы и руки. Этот рычаг может быть длиной ручки ключа или радиусом турбинного колеса.
Тангенциальная составляющая силы в виде крутящего момента может иметь два направления. В зависимости от направления этот силовой момент может увеличивать или уменьшать скорость вращения тела.
Момент силы относительно оси
Определение
Часто нет необходимости знать все компоненты момента силы относительно выбранной точки, а только момент силы на выбранной оси.
Тяга силы на оси — это проекция момента импульса на любую точку, принадлежащую оси.
Он направляет единичный вектор вдоль вала. Тогда пусть это будет одна АРБИТРАЖНАЯ интенциональная точка, принадлежащая ей. Вращающий момент мощности вала является следующим пошаговым продуктом. Это определение обусловлено тем, что две точки, принадлежащие валу и ‘s, проекции вращения равны. Давайте покажем.
Давайте воспользуемся векторным уравнением:?. Постепенно умножим это уравнение на единичный вектор, индуцированный вдоль оси. Это происходит потому, что вектор параллелен оси. Поэтому. То есть проекция крутящего момента на ось равна по точкам и ‘, принадлежащим оси.
Свойства
Упор оси от силы, линия действия которой через эту ось равна нулю. Доказательство с.
Вращающий момент вокруг оси от силы, параллельной этой оси, равен нулю. Доказательство с.
Доказательство свойств
Перемещение точки приложения силы вдоль линии ее действия
Все свойства силы не изменяются, если точка приложения силы перемещается вдоль линии действия, например, импульс с движением.
Предположим, что сила приложена к точке a. Проведите прямую параллельно вектору силы через точку a. Эта линия является линией действия власти. Переместите точку А при приложении силы к точке А’, которая принадлежит линии действия. Итак Вектор проектируется через две точки панели действий. Таким образом, его адрес соответствует управлению вектором силы. Тогда λ — это параметр. Если точка a ‘ смещена относительно A в направлении вектора. По-другому, .
Таким образом, вектор от o до a ‘ имеет вид. Найдем импульс силы, приложенной к A ‘ и применим свойство векторного произведения. Мы обнаруживаем, что импульс остается неизменным.
Абсолютная величина момента силы
Все свойства таковы, что абсолютное значение момента силы относительно точки равно произведению абсолютного значения плеча силы на выбранную точку.
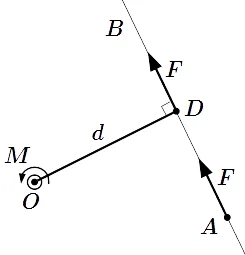
Абсолютное значение импульса m в точке O равно произведению силы f на рычаг d = | od | .
Предположим, что в точке A приложена сила. Исследуйте момент этой силы относительно точки O. Обратите внимание, что точки O, A и вектор лежат в одной плоскости. Пусть это показано на диаграмме. Проведите прямую AB через A и в направлении вектора. Эта линия называется линией электропередачи. Проведите перпендикуляр OD через O к линии действия. Пусть D — это пересечение линии действия и вертикальной линии. Далее — плечо силы относительно центра O. Это символизирует. Воспользуемся предыдущим свойством ⇑. Это позволяет перемещать точку действия силы вдоль ее линии действия. Перейдем к пункту D. Момент силы:. Поскольку он перпендикулярен вектору, из свойства векторного произведения следует, что абсолютное значение импульса равно где — абсолютное значение силы.
Обратите внимание, что вектор крутящего момента перпендикулярен плоскости на диаграмме. Его направление определяется правилом правого винта. Если мы повернем винт через точку C перпендикулярно плоскости фигуры в направлении силы F, винт будет двигаться к нам. Поэтому вектор момента перпендикулярен плоскости фигуры и направлен в нашу сторону.
Момент относительно точки от силы, проходящей через эту точку
Все свойства момента относительно точки O, т.е. силы, линия действия которой проходит через эту точку, равны нулю.
Линия действия силы должна проходить через точку O. В этом случае плечо силы относительно O равно нулю. Согласно предыдущему свойству ⇑, абсолютное значение момента силы относительно выбранной точки равно нулю.
Момент суммы сил, приложенных в одной точке
Импульс от векторной суммы сил, приложенных к точке во всех телах свойств ⇑ равен векторной сумме моментов каждой из сил, приложенных к той же точке.
Предположим, что к точке A приложены силы. Пусть будет векторная сумма этих сил. Из векторной суммы сил, приложенных к точке A, получаем импульс в точке O. Для этого мы применяем свойство векторного произведения.
Момент системы сил, векторная сумма которых равна нулю
Если векторная сумма всех сил свойств ⇑ равна нулю: сумма моментов этих сил не зависит от положения центра, при котором вычисляются моменты.
При непосредственной оценке эксплуатационных параметров автомобиля и его двигателя значения крутящего момента превалируют над значениями мощности. Среди двигателей с примерно одинаковыми конструктивными и эксплуатационными параметрами предпочтительнее двигатели с более высоким крутящим моментом.
Момент силы и правило моментов
М — крутящий момент. Единицей измерения является ньютон на метр (Н∙м). Направление вектора импульса всегда совпадает с направлением вектора силы. D — плечо силы. Единицей измерения является градус измерения (м).
Силовой рычаг — это кратчайшее расстояние между вращающимся валом и силовой линией.
Пример 1. Стальной шарик массой 2 кг вибрирует на струне длиной 1 м. Чему равен момент силы тяжести относительно оси, проходящей через точку O перпендикулярно плоскости в положении, показанном на рисунке?
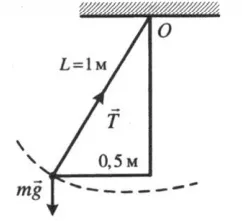
Плечо силы тяжести, или кратчайший путь от прямой, проходящей через точку О перпендикулярно плоскости до линии силы тяжести, — это часть, равная максимальному отклонению шарика от положения равновесия. Поэтому:.
Импульс силы может быть положительным или отрицательным.
Если сила заставляет тело вращаться по часовой стрелке, то этот импульс считается положительным.
Если сила заставляет тело вращаться против часовой стрелки, то этот импульс считается отрицательным.
Правило моментов
Объект с фиксированной осью вращения находится в равновесии, если алгебраическая сумма моментов всех сил, приложенных к объекту относительно этой оси, равна нулю.
В качестве альтернативы правило крутящего момента можно сформулировать следующим образом.
Сумма моментов сил, вызывающих вращение тела по часовой стрелке, равна сумме моментов сил, вызывающих левое вращение тела.
∑ m p r. = ∑ m p r. p r.
Условия равновесия тел
∑ → f i = 0; → v o = 0 и ∑ → f i = 0; → v o = 0
Простые механизмы — это устройства, которые помогают преобразовывать силы. К ним относятся рычаги, наклонные уровни, блоки, клинья и ворота.
Наклонная плоскость
Выгодные приобретения. Чтобы поднять груз на высоту h, необходимо приложить силу, равную его силе тяжести. Однако, используя наклонную плоскость, к полутону на уровне угла наклона можно приложить силу, равную произведению силы тяжести.
Рычаг
Обеспечьте прирост мощности, равный отношению второго силового плеча к первому плечу.
Неподвижный блок
Изменяет направление действия силы. Коэффициенты силы и плечи равны:.
Подвижный блок
Разделяет силу на две равные части, направление которых зависит от геометрии клина.
С помощью простого механизма сила набирается, но теряется. Поэтому при использовании простого механизма нет никакого выигрыша в производительности.
Задание EF22660
Алгоритм решения.
Мы знаем только массу сковороды: m1 = 0,8 кг; однако мы можем также представить плечи, обусловленные силой тяжести хлеба и буханки. Для этого длину линейки принимаем за единицу. Поскольку линейка разделена на 10 отрезков, можно предположить, что длина каждого отрезка равна 0,1. Тогда гравитационные плечи сковороды и рыбы будут равны друг другу.
Гравитация равна произведению массы на ускорение свободного падения. Поэтому.
M 2 = M 1 D 1 D 2. = 0, 8-0, 3 0, 4. = 0, 6 (k g)
Обсуждение: Алиса Никитина |Discussuss the analysis|Evaluation
tr. Прохождение через точку вокруг оси3 Перпендикуляры в плоскости чертежа равны.
Алгоритм решения.
- Сформулировать определение плеча силы.
- Найти плечо силы трения и аргументировать ответ.
Плечо силы трения — это кратчайшее расстояние от оси вращения до прямого объекта, на который действует сила. Чтобы найти это расстояние, необходимо провести перпендикуляр от точки равновесия к линии силы трения. Расстояние между этой точкой и линией — это плечо силы трения. На диаграмме этот участок соответствует линии o3В.
Теперь рассмотрим другую, более сложную задачу, в которой необходимо учесть силы трения для расчета равновесия системы объектов. Предположим, продавец решил разместить вывеску с переносной лестницей, как показано на рисунке 10.10.
Знак момента силы
Тангенциальная составляющая силы в виде крутящего момента может иметь два направления. В зависимости от направления этот силовой момент может увеличивать или уменьшать скорость вращения тела.
Чтобы проиллюстрировать это различие, вводятся характеристики крутящего момента.
Поскольку угол на уровне координат измеряется в направлении часового маркера, момент силы, вращающей тело в этом направлении, считается положительным. Если вращающий момент вращает тело по часовой стрелке, то он считается отрицательным.
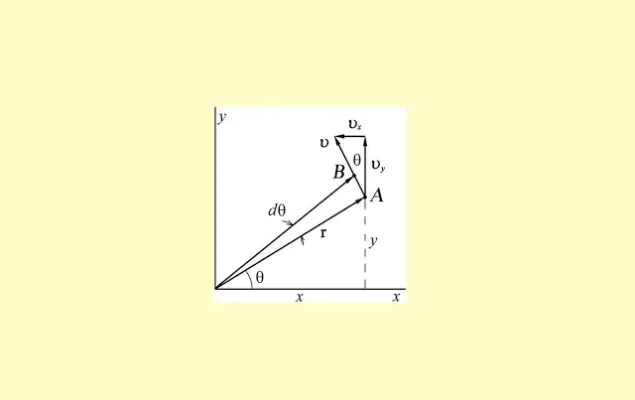
Рисунок 3.Угол поворота.








