Она приобрела огромную ценность. По сравнению с моментом инерции вокруг оси Земли, он составляет одну миллиардную часть от расчетного значения. Поэтому подход с использованием точек массы очень подходит для рассматриваемой проблемы.
Единицы измерения момента инерции
Момент инерции объекта, вращающегося вокруг оси, — это физическая величина ($ J $), равная значению момента инерции.
где
Значение момента инерции может быть измерено теоретически в соответствии с уравнением. Для этого объект, движущийся обычным способом, разлагается на более мелкие элементы, масса которых выражается в дм. Наконец, момент инерции (MI) равен произведению всех масс на расстояние от оси и считается квадратичным.
[H1toH2]
Килограмм, умноженный на метр в квадрате — единица измерения момента инерции в системе СИ
Самый простой способ измерить момент инерции объекта — рассмотреть точку массы, вращающуюся вокруг неподвижной оси.
Здесь $m$ — масса точечного материала. $r$ — это расстояние точки от оси вращения.
Из уравнения (3) следует, что
Квадратный килограмм-метр — это единица измерения момента инерции в Международной системе единиц. Эта единица взята из системы СИ. Квадратный килограмм-метр — это момент инерции массы в 1 килограмм, движущейся по окружности радиусом 1 метр вокруг оси вращения.
Грамм — сантиметр в квадрате — единица измерения момента инерции в системе СГС
Учитывая, что основными единицами измерения в системе СГС являются сантиметры, граммы и секунды, используя определение момента инерции материальной точки (3), предполагается, что грамм равен сантиметру. Квадрат — это единица измерения момента инерции системы СГС.
Один грамм, умноженный на квадрат одного сантиметра, — это момент инерции точечного материала массой один грамм на расстоянии одного сантиметра от оси вращения.
Квадратный грамм-сантиметр связан с единицей измерения момента инерции в системе СИ следующим образом.
Момент инерции, не имеющий единицы измерения
Размерные моменты инерции используются для изучения и описания движения и структуры небесных тел (планет, спутников и т.д.). Размерный момент инерции — это физическая величина, равная отношению момента инерции объекта радиуса $r$ и массы $m$ к моменту инерции точечного материала массой ($m$). Она вращается вокруг оси, расположенной на расстоянии $r$ от точки. Размерный момент инерции представляет собой распределение массы по глубине.
Сфера с тонкими стенками имеет безразмерный момент инерции, равный $ \frac$. Если масса тела сосредоточена вблизи центра тела, то безразмерный момент инерции меньше. Для луны с почти однородной структурой безразмерный момент инерции равен 0,391. Для Земли с плотным ядром безразмерный момент инерции равен 0,335.
i$ — масса $i$ — той материальной точки, которая является частью рассматриваемого тела; $r^2_i$ — расстояние в квадрате от $i$- той материальной точки до оси вращения тела.
В этом случае количество материальных точек, на которые делится тело, равно $k$. Если тело непрерывно и однородно, то
где $r$ — функция положения материальной точки в пространстве- $
Примеры задач с решением
ho$ — плотность объекта- $dV$ — объем элемента объекта.
Задание. Из основных законов динамики вращательного движения следует, что является единицей измерения момента инерции точки массы, вращающейся вокруг неподвижной оси?
Решение. Выражение для закона вращения динамики точки массы имеет вид
Где $ \начертание $ — полный импульс силы, действующей на точку. $ \ надпись $ это угловое ускорение, с которым движется точка. ( Выразите момент инерции из (2.1).
Единицами измерения силы-крутящего момента в системе СИ являются
Угловое ускорение точки массы находится следующим образом
где $ a_ $ — тангенциальное ускорение точки; R — радиус окружности, по которой движется точка.
Согласно уравнению (1.3), мы имеем
Ответ. Исходя из основных законов динамики вращения, в системах СИ момент инерции измеряется в килограммах на 1 квадратный метр.
Работа. Вычислите момент инерции Земли относительно оси вращения. Предположим, что масса Земли и ее радиус известны. ($ M_Z = 5,97 \ cdot ^ кг; \ R_Z = 6371 \ км $). Выразите момент инерции в $t\ cdot m ^ 2 $ (тонны на квадратный метр).
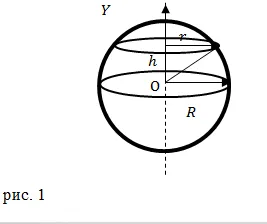
Решение. Рассмотрим Землю как однородную сферу. Найдите момент инерции шара относительно оси, проходящей через его центр. Разделите сферу на диски толщиной $dh$ (рис. 1), изменяйте радиус диска ($ r)™ и сделайте плоскость диска перпендикулярной оси вращения.
(Запишите основной момент инерции (диска) следующим образом.
Масса имеющегося диска ($ dm = \ rho dV $) составляет
\ dm = \ rho \ pi r ^ 2dh \ слева (2,3 \ справа). \ dm = \ rho
Получите момент инерции сферы относительно оси, проходящей через центр тяжести, и дополните уравнение (2.4) объемом сферы.
Плотность однородной сферы равна
Уравнение (2.5) преобразуется в следующий вид
Наконец, запишите уравнение для момента инерции земной сферы следующим образом
Вычислите момент инерции Земли.
Чтобы выразить момент инерции как $t\ cdot m ^ 2 $, используйте следующее соотношение
\ 1 \ т = 1000 \ кг, ᢙ следовательно, ᢙ 1 \ т \ cdot m ^ 2 = 1000 \ кг \ cdot m ^ 2. \

Ответ. $ J = 9,7 \ cdot ^ t \ cdot m ^ 2 $
[/H1toH2]
Мы уже помогли 4 372 школьникам и студентам сдать на отлично письменные работы от решения задач до дипломной работы! Узнайте, сколько стоит ваша работа за 15 минут!
Что такое инерция
Каждое тело продолжает сохранять состояние пологого или равномерного, линейного движения до тех пор, пока приложенная сила не заставит его изменить это состояние.
Согласно определению инерции в физике, это способность тела сохранять состояние покоя или движения в отсутствие внешней силы.
Определение момента инерции
Момент инерции — другое дело, когда само понятие инерции интуитивно понятно. Согласитесь, трудно представить это существо в своем воображении. В этой статье вы узнаете, как решить базовую задачу «момент инерции».

Из школы мы знаем, что масса — это мера инерции тела. Если вы толкаете две тележки разной массы, то остановить более тяжелую тележку будет сложнее. Другими словами, чем больше масса, тем больше внешняя сила, необходимая для изменения движения тела. Это относится к примеру коляски, движущейся вперед при движении по прямой.
По аналогии с массой и движением транспорта, момент инерции — это мера инерции объекта во вращательном движении вокруг оси.
Момент инерции является масштабной физической величиной и представляет собой меру инерции объекта при вращении вокруг оси. Он обозначается буквой J и измеряется в килограммах на квадратный метр в системе СИ.
Как рассчитывается момент инерции? В физике существует общая формула, используемая для расчета момента инерции любого объекта. Если объект разделен на мелкие части массой dm, то момент инерции равен произведению этих основных масс на квадрат расстояния от оси вращения.
Теорема Штейнера
Это общая формула для момента инерции в физике. Для массы m, вращающейся вокруг оси на расстояние r, это уравнение принимает вид
От чего зависит момент инерции? Для масс, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера — очень важная теорема, часто используемая при решении задач.
Кстати, для наших читателей действует скидка 10% на все работы!
Теорема Гюйгенса-Штайнера гласит.
Момент инерции тела вокруг любой оси равен произведению суммы момента сил тела вокруг оси, проходящей через центр масс вдоль любой оси, и веса квадрата расстояния.
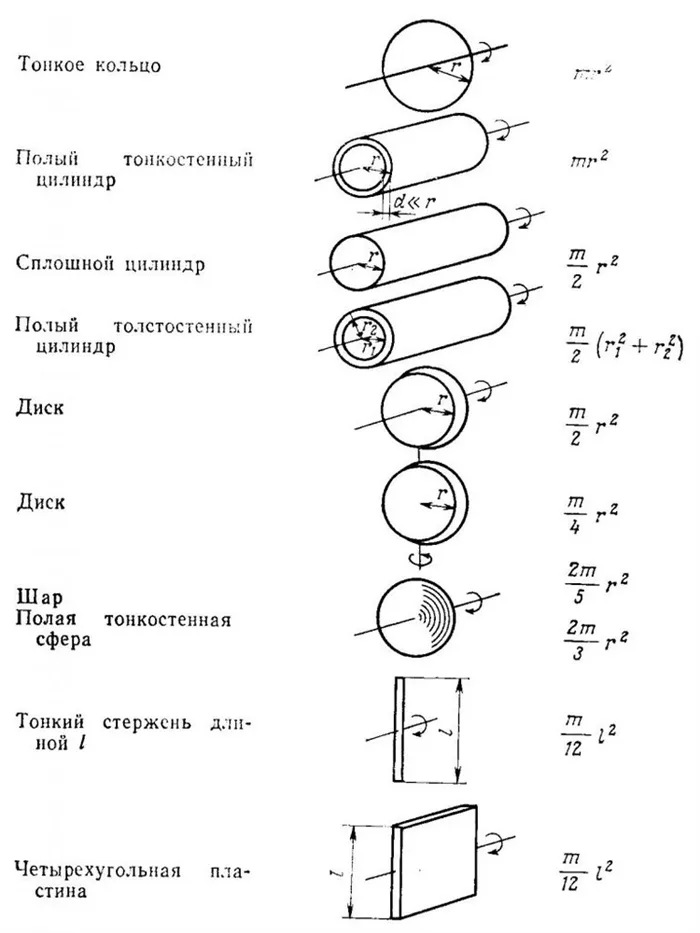
Примером движения по инерции является также движение молекул газа -каждая молекула в интервале времени между двумя последовательными столкновениями с другими молекулами движется по инерции.
В чем измеряется момент инерции тела?
Для тех, кто не хочет постоянно доводить до конца решение задачи и нахождение момента инерции, приведем рисунок, показывающий момент инерции однородного тела.
Получив необходимую теоретическую информацию о размере I, каждый может легко ответить на вопрос. Действительно, на вопрос о том, как измеряется тенденция осевой инертности при рассмотрении типа точечного материала I, следует ответить в килограммах на квадратный метр. Эта единица сокращенно обозначается как кг*м2. Очевидно, что если вы используете общее представление через объем и плотность, то у вас будет одна и та же единица измерения.
Обратите внимание, что Kg*M2 можно записать как M2*kg. Эта форма символизма также приемлема, но не используется в реальной физике.
Кг*М2 также является неактивной единицей СИ, поскольку и килограмм, и мера являются системными единицами массы и длины.
Пример задачи
Исследуемую единицу не следует путать с другой единицей, определяемой как кг/м2. Хотя это редко используется и не является единицей СИ, соответствующее давление можно рассчитать, умножив его на ускорение силы тяжести.

Теперь, когда мы знаем, как измеряется момент инерции и как он рассчитывается, мы можем решить следующую задачу Предполагая, что это материальная точка, необходимо определить неактивный момент планеты.
Для успешного решения этой задачи необходимо знать только два параметра: массу планеты и центральный радиус ее солнечной орбиты. Оба значения можно найти в соответствующих справочниках. Масса M и радиус Земли равны:.
Вычисление момента импульса материала точки с помощью уравнения приводит к следующему результату
Она приобрела огромную ценность. По сравнению с моментом инерции вокруг оси Земли, он составляет одну миллиардную часть от расчетного значения. Поэтому подход с использованием точек массы очень подходит для рассматриваемой проблемы.
Мы получили огромную ценность. По сравнению с моментом инерции Земли относительно оси, это в миллиарды раз меньше расчетной цены. Поэтому подход с использованием точечного материала хорошо подходит для рассматриваемой проблемы.
Виды моментов инерции
Как показано во втором типе, для тела постоянной массы ускорение тела (скорость изменения его скорости) прямо пропорционально приложенной к телу силе (толчок, тем быстрее тело ускоряется) и обратно пропорционально его массе (чем тяжелее тело, тем больше оно ускоряется).
- центробежный МИ;
- главный МИ;
- геометрический МИ;
- МИ относительно плоскости;
- центральный МИ;
- тензор инерции;
- эллипсоид инерции.
Помимо инерционного крутящего момента, существуют понятия в физике.
Центробежные MI относительно прямоугольных координатных осей (декартова система) равны jxy, jxz и jyz. Бычья ось является главной осью, когда центробежные моменты jxy и jxz равны нулю.
Любая часть тела может быть центром трех главных осей бездействия. Она характеризуется взаимной перпендикулярностью. Главными осями субъекта считаются. Главные оси, проходящие через центр масс, являются главными центральными осями неактивности объекта. МИС, связанная с ними, является главной центральной МИС. Для однородных тел осью симметрии всегда является инертная центральная ось.
Существует два типа геометрических MIS, основанных на объеме относительно оси и площади относительно оси.
Твердое тело может иметь MI относительно плоскости. Таким образом, это скалярная величина, рассчитываемая путем суммирования произведения массы каждой точки объекта и ее расстояния от плоскости в квадрате.
Момент инерции тела относительно оси вращения
Понятие «центральный МИ» связано с точкой О, МИ относительно полюса или полярным МИ.
MI служит мерой инерции тела, вращающегося вокруг оси, так же как масса является мерой при поступательном движении.
Формула Штейнера позволяет определить MI объекта относительно оси вращения.
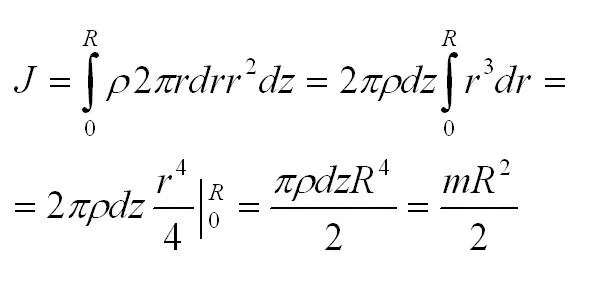
Моменты инерции простейших объектов
Наглядной демонстрацией применения формулы Штейнера является расчет MI стержня, ось вращения которого проходит через конец.
- МИ точечного предмета либо полого цилиндра с тонкими стенками (с массой m и радиусом r) = mr 2
- МИ диска или сплошного цилиндра = 1/2 mr 2
- МИ цилиндра с толстыми стенками, у которого внешний радиус обозначен r2Момент инерции некоторых однородных тел простой формы, в зависимости от характеристик осей вращения, можно определить по следующим формулам1а внутренний — r

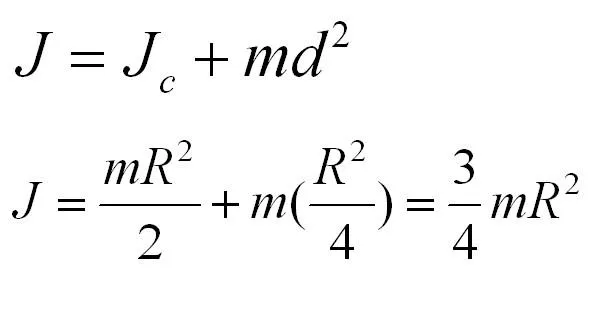
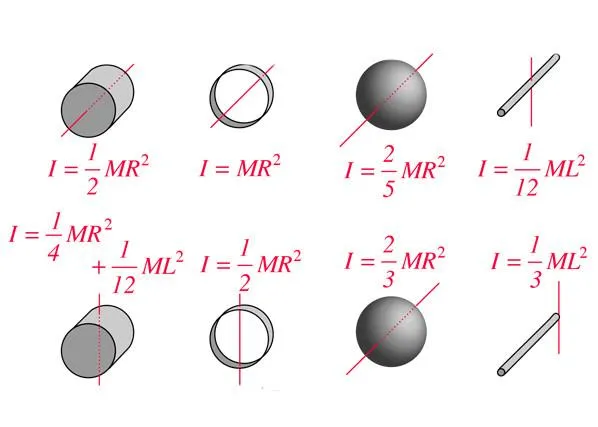

, :
Мир не идеален
В случае движения мы берем ту часть первого закона Ньютона, в которой скорость постоянна, но не равна нулю. Здесь мы обнаружим способность тела двигаться, которая была вызвана силой, прекратившей свое действие на тело.
К сожалению, а может быть, к счастью, мы не живем в мире, где все тела движутся прямолинейно и равномерно. Из-за этого инерция невозможна в реальной жизни, потому что всегда есть трение, сопротивление воздуха и другие факторы, препятствующие движению.
Пуля, выпущенная из пистолета, будет продолжать двигаться, сохраняя свою скорость, если на нее не будет действовать другое тело — воздух. Поэтому скорость пули уменьшается.
Велосипедист, который перестал крутить педали, сможет сохранить свою скорость, если на велосипеде не будет трения. Поэтому, если педали не нажаты — скорость велосипедиста снижается и останавливается.
Вопросы
Поскольку вращающееся тело может иметь форму, отличную от точки или маленькой сферы, формула для момента инерции может иметь другую форму для более точных расчетов.

1. Посмотрите на рисунок с формулами для вычисления момента инерции для тел различной формы. Как вы думаете, какая формула лучше всего подходит для расчета момента инерции маховика автомобиля? Варианты ответа: a, b, c, d, e, f, g, h или i
車

2. Два волнореза одинаковой массы вращаются с одинаковой угловой скоростью, но диаметр первого волнореза меньше диаметра второго. Кто из них падет раньше?








