Поэтому перемещение является векторной величиной. Действительно, чтобы понять, как двигалось тело, нужно знать не только расстояние от начальной точки, но и направление, в котором оно двигалось.
Что такое путь в физике и как его обозначают? Формулы и пример задачи
Кинематика — одна из ключевых областей техники, которая занимается изучением законов движения тел (причины движения изучает динамика). В этой статье рассматривается одна из ключевых величин кинематики и задается вопрос: «Каков путь к физике?». и отвечает на вопрос.
Каков путь к физике? Это величина, равная длине участка пространства, пересекающего исследуемое тело во время его движения. Чтобы рассчитать маршрут, необходимо знать исходное положение тела, а также траекторию его движения. На вопрос о том, что такое путь в физику, можно ответить по-разному. Под этим размером понимается длина траектории, т.е. воображаемой линии, вдоль которой двигалось тело.
Для объявления маршрута используются различные символы. Например, если вы говорите о движении в одном измерении, вы можете использовать символ DX Здесь D представляет собой изменение координаты x. В дополнение к этому символу для обозначения рассматриваемой величины часто используются буквы s, L и H, последние означают длину и высоту соответственно. Таким образом, в кинематике буква s является наиболее распространенным обозначением пути.
Если известно, что тело движется вдоль прямой линии в трехмерном пространстве и известны координаты его исходного (x0; y0; z0) и конечного (x1; y1; z1) положений, то можно определить маршрут. С помощью прессы
s =√ ((x1 -x0)2 + (y1 -y0)2 + (z1 -z0)2)
Формулы кинематики

Рассмотрев, как символизируется физический путь и какова эта величина, мы приводим несколько видов кинематики, используемых для расчета свойств изучаемых движений. Эти типы следующие.
где первое уравнение соответствует случаю, когда тело движется равномерно по прямой со скоростью V в момент времени t. Второе уравнение применимо к равноускоренному движению. Здесь V0 и символ обозначают начальную скорость и ускорение, соответственно. Символ плюс следует использовать, если тело ускоряется, а символ минус — если тело замедляется.
Пример задачи
Проанализируйте физический путь и решите следующие задачи. Лодка со скоростью 13 км/ч движется против течения реки из одного пункта в другой в течение 1,5 часов. Какое расстояние пройдено, если скорость реки 3 км/ч?

Это типичная проблема применения типа к равномерному движению тела. Единственная сложность в решении этой задачи — определение фактической скорости лодки. При движении против течения разница равна 13-3 = 10 км/ч. Затем нужно подставить известные значения типа s, чтобы получить ответ.
s = v x t = 10 км/ч x 1,5 ч = 15 км
В вопросе о расчете маршрута обратите внимание на единицы измерения скорости, времени и ускорения, которые необходимо использовать, чтобы избежать ошибок.
Рассмотрев, как символизируется физический путь и какова эта величина, мы приводим несколько видов кинематики, используемых для расчета свойств изучаемых движений. Эти типы следующие.
Механическое движение. Траектория. Путь. Перемещение

1. механическое движение, которое представляет собой изменение положения тела в пространстве относительно других тел с течением времени. Существуют различные типы инженерии. Если все части тела движутся одинаково, а линии, вписанные в тело, параллельны сами себе, то такое движение называется специфически-фористическим (рис. 1).
Точки вращающегося колеса описывают окружность вокруг оси колеса. Все колесо и все его точки находятся во вращательном движении (рис. 2).
В случае тела, например, сферы, висящей на нити, оно отклоняется от вертикального положения в одну или другую сторону, и его движение носит колебательный характер (рис. 3).
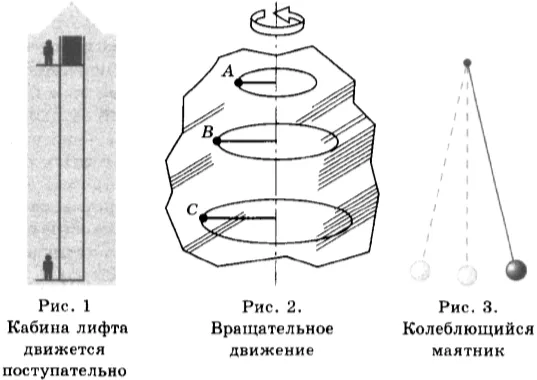
2. определение механического движения включает термин «по отношению к другому телу». Это означает, что конкретное тело может оседать по отношению к другому телу и двигаться по отношению к другому телу. Например, пассажиры, сидящие в автобусе, движущемся по отношению к зданию, также движутся по отношению к ним, но более спокойно по сравнению с автобусом. Река в реке не движется по отношению к воде, но она движется по отношению к берегу (рис. 4). Поэтому, говоря о механическом движении тел, мы должны определять тела в зависимости от того, движутся они или оседают. Такой орган называется эталонной системой. В примере с движущимся автобусом, приведенном выше, в качестве системы отсчета можно выбрать дом, дерево или столб рядом с автобусной остановкой.

Для определения положения тела в пространстве вводится система координат и соединяется с системой отсчета. Если движения тела изучаются по прямой линии, используется одномерная система координат. Это означает, что система отсчета связана с системой координат с одной координатной осью. Ось коровы (рис. 5).

Если тело движется по криволинейной траектории, то положение тела характеризуется двумя координатами X и Y, поэтому система координат уже двумерна (рис. 6). Такими движениями являются, например, движение мяча от футбольного мяча или стрелы, пущенной Стрельцом.
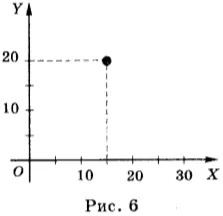
Если рассматривать движение тела в пространстве, например, движение аэроплана, то система координат, связанная с системой отсчета, состоит из трех вертикальных координат (OX, OY, OZ) (рис. 7).
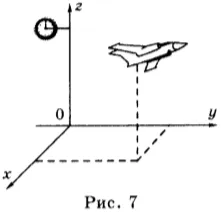
Когда тело движется, его положение в пространстве, т.е. координаты, меняется со временем и требует наличия органа (часов) для измерения времени и определения момента времени, соответствующего какой координате.
Поэтому для определения положения тела в пространстве и изменения этого положения во времени необходима система отсчета, связанная с ней система координат, т.е. часы, которые в совокупности составляют систему измерения времени. Система отсчета (рис. 7).
ПРИМЕРЫ ЗАДАНИЙ
1. эталонная основа.
1) только один кадр 2) один кадр и система координат 3) один кадр и часы 4) кадр, система координат и часы.
Соответствующие значения: a. корень — b. сдвиг. Правильные ответы: 1) 2) только b
1) только a) b 3) и a и b 4) ни a, ни b
3. пассажиры метро стоят на пологой лестнице, уходящей вверх. Они не движутся по отношению к
1) другие спускающиеся пассажиры, стоящие на той же подкатной лестнице 2) другие пассажиры, стоящие на той же подкатной лестнице 3) пассажиры, поднимающиеся по той же подкатной лестнице 4)
4Что представляет собой кузов автомобиля, движущегося по автостраде?
1) по отношению к другому автомобилю, движущемуся в противоположном направлении с той же скоростью 2) по отношению к другому автомобилю, движущемуся с той же скоростью в том же направлении 3) по отношению к одному фонарю 4) по отношению к пешеходу, идущему по дороге)
5. два автомобиля движутся с одинаковой скоростью 20 м/с в одном направлении относительно Земли. Какова скорость одного автомобиля в системе отсчета по отношению к другому автомобилю?
1) 0 2) 20 м/с 3) 40 м/с 4) 20 м/с
6. два автомобиля движутся навстречу друг другу с одинаковой скоростью 15 м/с относительно Земли. Какова скорость одного автомобиля в системе отсчета по отношению к другому автомобилю?
1) 0 2) 15 м/с 3) 30 м/с 4) 15 м/с
7.Какова орбита точки на лопасти винта летящего вертолета относительно Земли?
1) прямая линия 2) круг 3) дуга 4) спиральная линия
8.Мяч падает с высоты 2 м, ударяется о пол и поднимается на высоту 1,3 м. Каковы путь \(l \) и перемещение \(s \) во время движения шарика?
1) \(l \)= 3,3 м, \(s \)= 3,3 м 2) \(l \)= 0,7 м, \(s \)= 0,7 м 4 ) \(l \)= 0,7 м, \(s \)= 3,3 м
9. решить две задачи. 1. вычислите скорость поезда между двумя станциями. 2. измерьте силу трения на поезде. При решении какой проблемы поезд может рассматриваться как точка качества?
1) только первый 2) только второй 3) первый и второй 4) ни первый, ни второй
10. Точка на колесе велосипеда представляет собой полуокружность радиуса ⌘ (r \), когда велосипед находится в движении. Чему равен путь ⌘(l \) точки на ободе и измерение перемещения ⌘(s \)?
1) \(l = 2R \), \(s = 2R \) 2) \(l = \ pi R \), \(s = 2R \) 3) \(l = 2R \), \(s = \ pi R \) 4) \(l = \ pi R \), \(s = \ pi R \)
11. соотнесите элементы знаний в левой колонке с понятиями в правой колонке. Под номером элемента в левой колонке таблицы введите соответствующий номер выбранной концепции в правой колонке.
Знание A) физического размера B) единицы размера C) средства измерения
Решение 1) траектория 2) маршрут 3) таймер 4) километр 5) опорная система координат
12.Соотнесите значения в левом столбце со свойствами значений в правом столбце. Под номером когнитивного элемента в левой колонке таблицы укажите соответствующий номер выбранного понятия в правой колонке.
Рассмотрев, как символизируется физический путь и какова эта величина, мы приводим несколько видов кинематики, используемых для расчета свойств изучаемых движений. Эти типы следующие.
Траектория пути
Кинематика изучает движение тела, независимо от причины этого движения. Основной задачей кинематики является математическое описание положения тела в исходной системе отсчета и изменение этого положения во времени.
Положение объекта в системе отсчета задается одной или несколькими координатами (в зависимости от количества измерений) и временем.
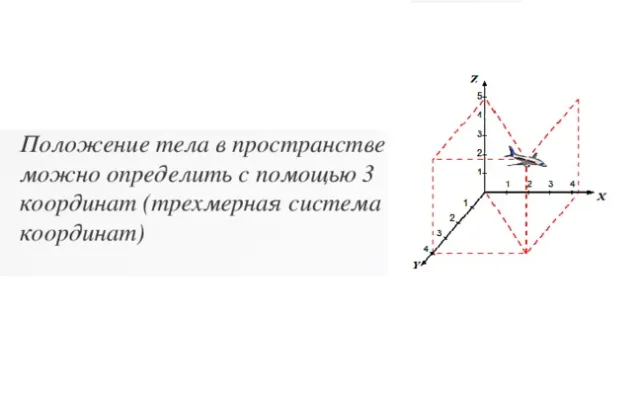
Рисунок 1. Координаты тела в пространстве.
При движении тела его координаты меняются со временем. Умножение скорости тела на время движения дает длину пройденного расстояния.
Однако знание момента времени, в который тело находилось в нулевой точке, не всегда позволяет нам определить положение тела в другой произвольный момент времени.
Дело в том, что с помощью приведенной выше формулы можно найти длину пройденного маршрута. Кроме того, сам путь может иметь любую форму, какой бы сложной она ни была. Линия, по которой движется тело, не обязательно должна быть прямой, это может быть круг, пунктирная линия или более сложная фигура, состоящая из множества частей.
Линия, по которой тело движется в течение всего времени, называется траекторией или просто траекторией.
Перемещение
Чтобы всегда знать, где находится тело в определенный момент времени, необходимо знать не длину пройденного расстояния, а другое кинематическое свойство — перемещение.
Перемещение — это вектор, соединяющий начальное и конечное положение тела.
Зная начальную точку в определенный момент времени и смещаясь к определенному времени, всегда можно найти координаты тела в конце пути.
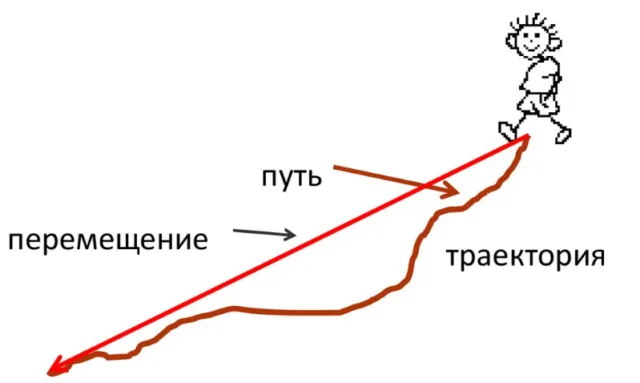
Рисунок 2.Корень и смещение.
Сходство и различие.
Корень и смещение — это не одно и то же. Если движение горизонтальное или криволинейное и криволинейное, длина пути всегда будет больше, чем измеренное перемещение. Это происходит потому, что вектор — это прямая линия, т.е. кратчайшее расстояние между двумя точками. Кривые пути не являются прямыми линиями.
Более того, хотя путь может быть длиннее, смещение может быть нулевым. Например, планета, движущаяся по кругу, будет проходить большое расстояние с каждым оборотом, но смещение никогда не превысит диаметр орбиты и может быть равно нулю, если планета полностью вращается.
Рисунок 3: Орбиты планет.
Однако и смещение, и путь служат одной и той же цели, т.е. описанию движения. Оба измеряются в единицах длины, и типы движения могут быть применены к обоим.
Однако траектория описывает весь путь тела, тогда как смещение фокусируется на разнице в положении тела между первым и последним моментами движения. Именно поэтому большинство видов кинематики со временем работают со сдвигами.
Единственный случай, когда путь и перемещение равны, — это случай линейного движения, когда знак скорости движения не меняется.
Это позволяет найти конечную точку каждого участка автобусного маршрута и конечную точку всего маршрута на основе начальной точки и перемещения, даже если маршрут не известен.
Закон сложения скоростей.
Подготовьте две системы отсчета. Один из них относится к фиксированной системе координат. Эта система отсчета символизируется и называется фиксированной. Вторая система отсчета, обозначаемая, относится к системе отсчета, которая движется относительно тела со скоростью. Эта опорная система координат называется подвижной. Кроме того, поскольку предполагается, что координатные оси систем движутся параллельно друг другу (координатная система не вращается), вектор можно считать скоростью движущейся системы относительно объекта.
Неподвижные системы координат обычно связаны с землей. Если поезд плавно и с высокой скоростью движется по рельсам, то эта система отсчета, связанная с вагонами поезда, будет являться движущейся системой отсчета.
Любая часть инвалидной коляски (кроме вагонов-струн!) Обратите внимание, что скорость поезда также равна скорости Если муха неподвижна в какой-то точке вагона, то она быстро движется относительно земли. Поскольку муха перевозится вагонеткой, скорость движущейся системы относительно объекта называется скоростью транспортировки.
Предположим, что муха ползет по вагону. Скорость мухи относительно вагона (т.е. в движущейся системе) символизируется и называется относительной скоростью. Скорость мухи относительно земли (т.е. в неподвижной системе) символизируется и называется абсолютной скоростью.
Давайте рассмотрим, как эти три скорости, абсолютная скорость, относительная скорость и скорость переноса, соотносятся друг с другом. На рисунке 4 муха характеризуется точкой. Кроме того — вектор радиусов точек в неподвижной системе — вектор радиусов точек в подвижной системе — векторная система радиусов рамок в неподвижной системе.
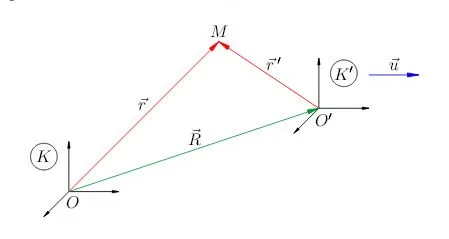 |
| Рисунок 4. |
Продифференцировав это равенство.
(Производная суммы равна сумме производных как в случае вектора, так и в случае масштабируемой функции). Производная — это скорость точки в системе, т.е. абсолютная скорость.
Аналогично, производная — это скорость точки в системе, т.е. относительная скорость.
В, это что; это скорость точки в неподвижной системе. Другими словами, это скорость перемещения мобильной системы относительно недвижимой системы.
(Вследствие (3) мы имеем
Дополнительный закон скорости. Скорость точки в неподвижной системе равна векторной сумме скоростей подвижной системы и скорости точки с точки зрения подвижной системы. Другими словами, абсолютная скорость — это сумма транспортной и относительной скоростей.
Таким образом, если муха врезается в движущийся вагон, то скорость мухи относительно почвы равна векторной сумме скорости вагона и скорости мухи относительно вагона. Интуитивно очевидный результат!
Виды механического движения.
Простейшее механическое движение материальной точки — это равномерное прямолинейное движение. Если измерение вектора скорости остается постоянным, движение называется равномерным (направление скорости может меняться).
Если направление вектора скорости остается постоянным, движение называется прямолинейным (величина скорости может меняться). Маршрут прямолинейного движения — это прямая линия, вдоль которой расположен вектор скорости. Например, автомобиль, движущийся с постоянной скоростью по проезжей части дороги, будет двигаться равномерно (но не по прямой). Автомобиль, разгоняющийся на прямом участке автострады, будет двигаться по прямой (но не ровной) линии.
Однако если движение тела остается стабильным как по скорости, так и по направлению, то движение называют прямолинейным.
В терминах вектора скорости для этих типов движений можно дать более короткие определения.
- равномерное движение
- прямолинейное движение
- равномерное прямолинейное движение
Наиболее важным частным случаем неравномерного движения является равновесие, когда измерение и адрес вектора ускорения остается постоянным.
Помимо материальных точек, в технике можно рассмотреть еще одну идеализацию: твердые тела. Твердое тело — это система материальных точек, расстояние между которыми не меняется со временем. Твердые модели используются, когда размеры тела нельзя игнорировать, но можно пренебречь изменениями размеров и формы тела во время движения.
Простейшими видами механического движения твердых тел являются удельные и вращательные движения. Движение тела называется ratio phor, если линия, соединяющая две части тела, движется параллельно исходному направлению. В движениях ratio phor траектории всех точек тела идентичны. Они взяты в параллельных смещениях друг к другу (рис. 5).
 |
| Рисунок 5. |
Движение тела называется вращательным, если все точки описывают окружность на параллельных уровнях. Центр этих циклов имеет прямой перпендикуляр на всех этих уровнях, и эта линия называется валом вращения.
Форма. 6 показана сфера, вращающаяся вокруг вертикальной оси. Это обычный способ проектирования сфер с соответствующими динамическими проблемами.








