Этот поток подчеркивает стохастические свойства всего магнита или других типов источников МП. Если индукция подчеркивает стохастические свойства своего эффекта в любой момент времени, поток становится цельным. Это вторая по важности функция в данной области. Если МИ выступает в качестве энергоблока для МП, то поток считается его энергетической линией.
Ток или поток? Магнитные цепи и их основные характеристики
Привет Хабр! Недавно я задумался об актуальности статьи и заметил, что на Хабре нет ни одной обзорной статьи по магнитным цепям. Почему ;! В конце концов, что это такое?
Наверняка даже самые далекие от техники инженеры имеют представление о том, что такое электрическая цепь, но о магнитных цепях они, возможно, вообще никогда не слышали. Каждый студент в какой-то момент видел в учебниках физики различные диаграммы и уравнения, объясняющие закон Ома. Однако магнитные цепи не являются частью учебной программы.
Я решил написать эту статью, чтобы показать, насколько прекрасен мир физики, и заинтересовать студентов в ее изучении. Конечно, для полноты картины в этой статье также будет обсуждаться выведение формул и использование математических операций, которые могут быть знакомы не всем, но я постараюсь сгладить эти моменты. Давайте начнем!
Что нужно вспомнить?
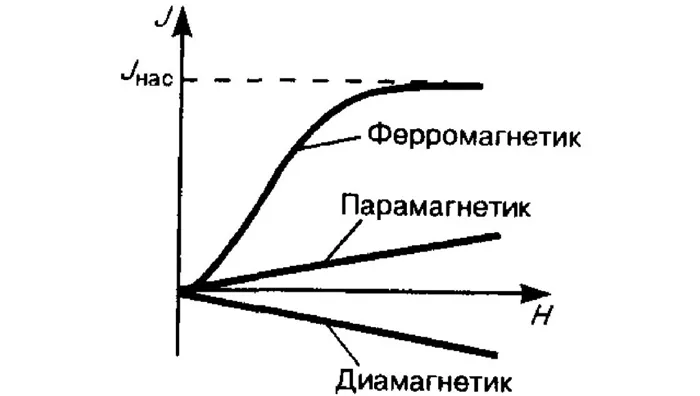
Чтобы объяснить эту статью более понятно, стоит вспомнить основные свойства самих магнитных полей (вектор магнитной индукции, вектор напряженности и поток вектора магнитной индукции). Вам также необходимо помнить некоторые вещи о магнитных материалах, т.е. ферромагнитных материалах.
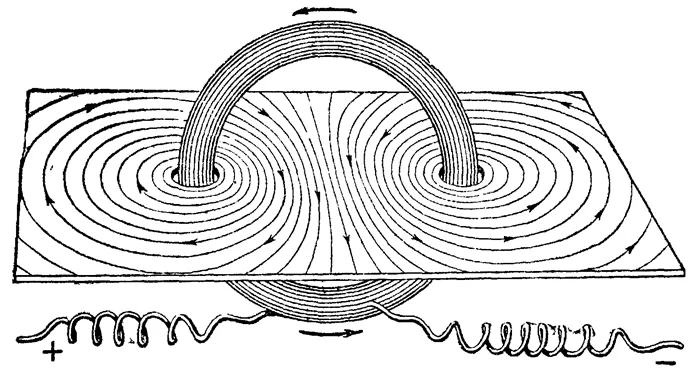
Вы, вероятно, знаете общий закон Ома и помните, что такое ток, напряжение и сопротивление. Если нет, то рекомендуется обратиться к внешнему источнику, чтобы хотя бы понять общие идеи о И.Е. настоятельно рекомендует Иродов, ‘Электромагнетика’.
Применение магнитных цепей
Магнитные цепи имеют очень широкий спектр применения. То есть, они используются для обеспечения прохождения магнитного потока через специальные проводники с малыми или, в некоторых случаях, с потерями магнитного потока. Взаимозависимость магнитной и электрической энергии и переходы из одного состояния в другое широко используются в электротехнике. Трансформаторы, различные электродвигатели, генераторы и другие устройства работают по схожим принципам.
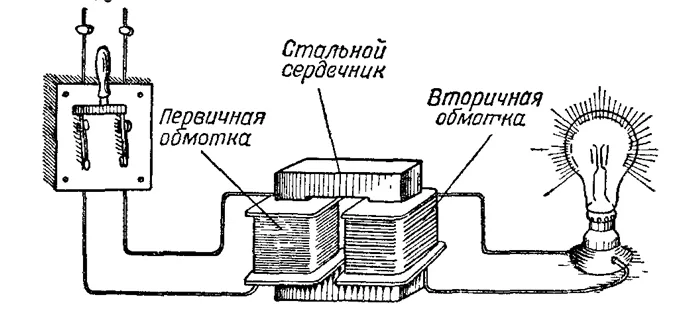
Конечно, мы могли бы продолжить разговор об устройствах и различных типах магнитных цепей (которые мы обсудим позже), но наша главная цель — рассмотреть сделанные выводы об основных свойствах магнитных цепей. Давайте двигаться дальше!
Энергия магнитного поля, используемая в данном эксперименте, характеризуется магнитной индукцией. Однако оказывается, что одной этой величины недостаточно при попытке объяснить наблюдаемые явления.
Магнитный поток простыми словами
Термин «поток» может ассоциироваться с течением воды. Количественная оценка этого потока означает конкретное количество воды, протекающей через участок в конкретной точке. Этот поток может нести большое или малое количество воды, в зависимости от скорости движения воды и поверхности этого участка.
Магнитный поток является физической величиной и тесно связан с явлением электромагнитной индукции. Это сложный размер и довольно абстрактный. Однако, как вы можете себе представить, его название происходит от механики жидкости. Здесь, однако, нет потока материала через поверхность, только векторы магнитной индукции B, которые «пронизывают» поверхность и в некоторых случаях «скользят» по ней.
Представьте себе однородное магнитное поле, описываемое вектором магнитной индукции B. Поместите плоскость с полем S в это поле совершенно произвольным образом, т.е. под произвольным углом к вектору B (рис. 1). Теперь определите вектор B, перпендикулярный плоскости поверхности. Сделайте длину этого вектора равной длине поверхности.
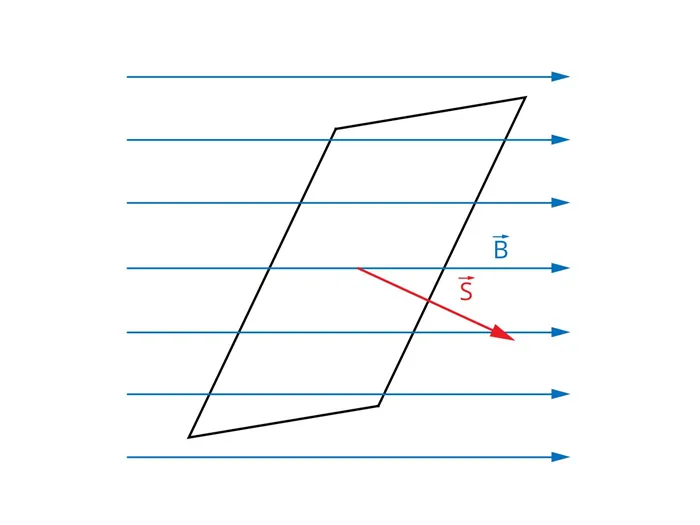
Рис. 1. Плоская поверхность в магнитном поле. Вектор S, представляющий поверхность, отмечен красным цветом.
Поток вектора магнитной индукции FB S через поверхность является степенным произведением векторов B и S.
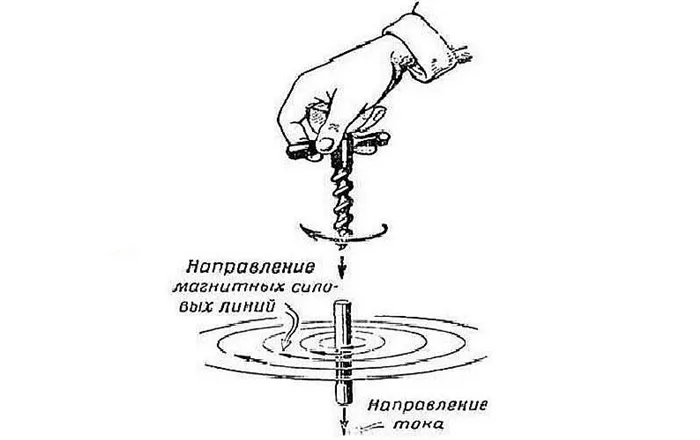
Поэтому можно дать следующее определение термина «магнитный поток
Магнитный поток — это поток вектора магнитной индукции B через поверхность. Для бесконечно малых площадей он равен произведению коэффициента| B | на синус угла α между площадью dS и n перпендикуляра к плоскости B и площадью. Для поверхностей конечных размеров она является суммой (интегралом) своих меньших частей.
Википедия.
Зависимости магнитного потока
Используя это уравнение, можно увидеть, что магнитный поток зависит от трех переменных: магнитного поля B, поверхности S и угла α.
Магнитный поток линейно зависит от B и S. Например, если площадь S увеличивается, но магнитное поле B и угол α остаются прежними, магнитный поток увеличится. Поэтому большая площадь поверхности приводит к большему магнитному потоку, а меньшая площадь поверхности — к меньшему магнитному потоку.
С другой стороны, при увеличении магнитного поля B магнитный поток также увеличивается. Сильные магнитные поля приводят к большим магнитным потокам, а слабые магнитные поля — к малым потокам.
В общем случае, чем больше магнитное поле B или площадь S, тем больше магнитный поток.
Ситуация с углом α немного сложнее. Представьте, что ваша поверхность перпендикулярна магнитному полю, а угол α = 0°. Здесь находится максимальный магнитный поток. Если вы увеличиваете угол с шагом здесь, магнитный поток уменьшается. При достижении α = 90° магнитный поток равен нулю, поскольку магнитное поле параллельно поверхности. Затем он снова начинает расти.
Примеры
Следующие примеры помогут вам лучше понять новую концепцию и скорость потока воды
2. что происходит в случае магнитной индукции?B = 0?
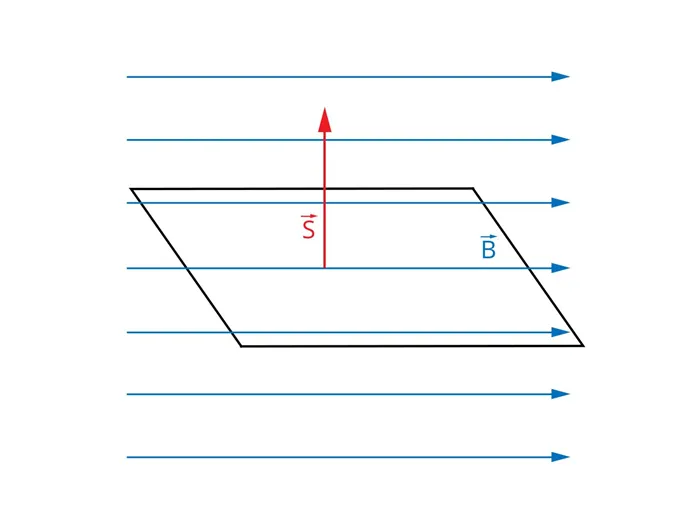
Рис. 3. Поверхность параллельна линиям магнитного поля. Векторы B и S перпендикулярны.
Определение магнитного потока показывает, что это происходит, если
cos90° = 0.
На рис. 3 показано, как в этом случае плоскость выравнивается по отношению к вектору магнитной индукции.
Обратите внимание, что FB который можно выразить как произведение B и S⟂где S⟂ = S*cosα. Аналогично, величина потока магнитного поля всегда может быть рассчитана путем умножения магнитной индуктивной составляющей, перпендикулярной поверхности, на размер поверхности (см. рис. 4a и 4b).
Рис. 4a. поверхность S⊥ — это проекция поверхности S в направлении, параллельном линиям магнитного поля (рис. 4b). Вектор B⟂ проекция вектора B на направление вектора S.
Если магнитное поле неоднородно или поверхность изогнута, как можно рассчитать поток магнитного поля? Поверхность, для которой необходимо рассчитать поток, делится на более мелкие участки, где можно предположить, что поверхность плоская и поле однородное. Все это делается для того, чтобы можно было применить определение потока. Затем рассчитываются и добавляются небольшие «потоки». Описанная процедура называется вычислением долей площади и описывается в следующей форме
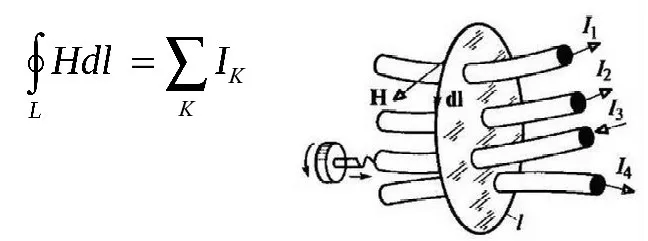
Вычисление таких интегралов вовсе не обязательно, но полезно понимать последствия такого процесса.
Источником магнитного поля (b) являются постоянные магниты. Они изготовлены из магнетита. В природе они известны как оксид железа. Это черный минерал с молекулярной структурой Feo-Fe2O3. Свойства магнитов известны давно. Магниты имеют два полюса — северный и южный.
Измерительные приборы
Магнитный поток можно измерить в лаборатории и в полевых условиях с помощью специальных органов, называемых расходомерами. Эти устройства также называются верберометрами. Особенностью этого измерительного устройства магнитной складчатой системы (MES) является то, что ток подается в каркас без катушки.
Предупреждение. Электричества нет, но индекс не имеет фиксированного положения на шкале.
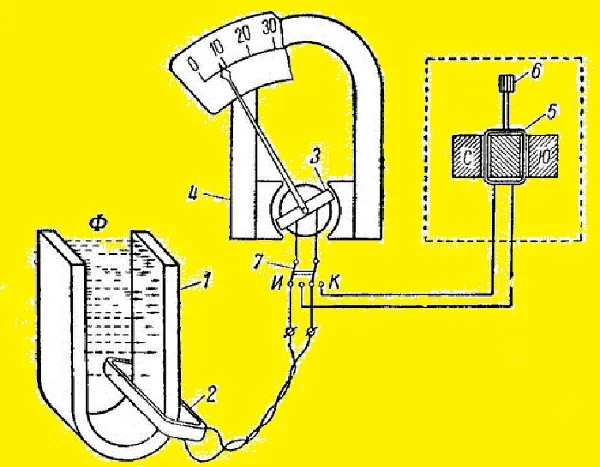
Устройство состоит из следующих частей, обозначенных на схеме выше.
- испытуемый постоянный магнит – 1;
- рамка измерительная – 2;
- рамка прибора – 3;
- магнит прибора – 4;
- рамка корректирующего устройства – 5;
- головка регулировки корректирующей рамки – 6;
- переключатель «работа – коррекция» – 7.
Ротометры не могут измерять пациентов с МФ из-за их низкой чувствительности.
Теорема Гаусса для магнитной индукции
Великий немецкий ученый Карл Гаусс, выдающийся в математике, физике и астрономии, вывел законы (теоремы) в области магнетизма. В нем говорится, что в отличие от электрического поля, создаваемого электрической нагрузкой, МП не создается магнитной нагрузкой. Они не существуют в классической электродинамике.
Информация. Теорема, экспортируемая GAUS, относится к основным законам электродинамики и является частью системы уравнений Максвелла. Она выражает связь между потоком напряженности электрического поля, проникающего через любую замкнутую поверхность, и суммой нагрузок, действующих на объем, описываемый поверхностью. Сумма выражается в алгебраической форме.
С точки зрения магнитной индукции, поток b → величина через замкнутую поверхность S имеет нулевое значение.
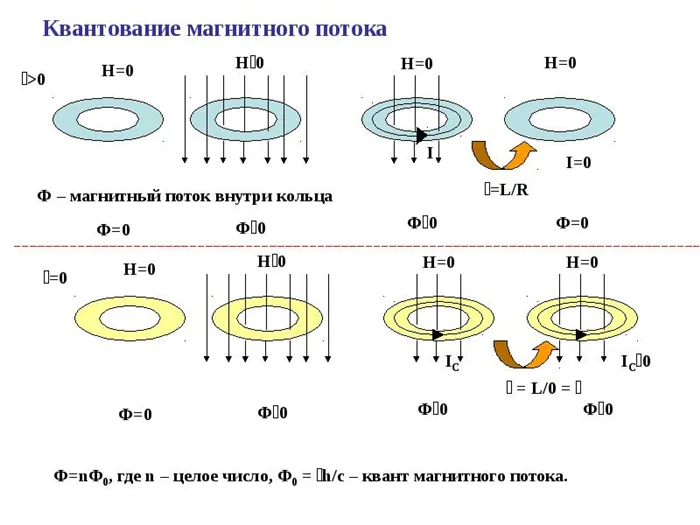
Квантование магнитного потока
В 1961 году было фактически обнаружено, что величина f умножает квантовый поток φ0 = h/2e = 2,067833758*10-15 ВБ, если магнитный поток направлен через сверхпроводник с петлей утечки электричества. Это цена системы СИ.
Такие эксперименты были проведены Дивером и Фэрбенксом в США. Они провели количественную оценку, используя полые трубки и пропуская через них круговые токи сверхпроводящей природы. Их квантовый результат был в два раза меньше. Это было связано с тем, что электроны внутри сверхпроводника были разбиты на пары. Частицы образовывали двойники с загрузкой 2e. Движение этих пар является свойством сверхпроводимости.
Для истории. Сверхпроводник — это материал, сопротивление которого быстро уменьшается при снижении температуры до определенного значения. Она практически равна нулю, и тогда можно говорить о сверхпроводящих свойствах. Металлы, которые являются отличными проводниками, такие как золото, серебро и платина, не приобретают гипертонических свойств в таких условиях.
ОТВЕТ: f = I I ‘µ 0 L 2 P 1 B -1 B +A. Магнитные силы толкают рамку с током наружу из-за ее первоначального направления по сравнению с полем провода.
Теорема Гаусса для магнитного поля
Значение полного магнитного тока через замкнутую поверхность равно нулю.
Уравнение ∮b→d s→= 0 применимо к каждому магнитному полю. Это уравнение считается теоремой Остроградского-Гаусса для электростатической материи в вакууме.
Запись ∮b→d s→= 0 показывает, что источником магнитного поля является ток, а не магнитная нагрузка.
Имеется бесконечно длинный прямой проводник с током I и квадратная рамка рядом. Кадр утекает по размеру текущего i ‘. Рама имеет одну сторону. Он находится на одном уровне с проводом, как показано на рис. 2. Цена расстояния от ближайшей стороны рамы до проводника равна b. Когда рамка будет удалена из поля, вы обнаружите, что магнитная сила работает. Ток следует считать твердым.
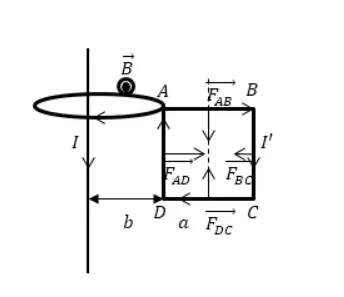
Индукция магнитного поля длинного проводника с током на участке, где находится квадратная рамка, направлена в сторону компании.
Рассмотрим рамки с токами в неоднородных полях. Это означает, что магнитная индукция уменьшается при удалении от проводника.
Давайте используем тип для магнитных токов и работу для их соединения.
a = i’ φ2 — φ1 (1. 1). Где i ‘ принимается за ток в рамке, а φ1 — за поток через квадратную рамку на расстоянии, равном b от сторон. φ2= 0. Это связано с тем, что конечное положение рамки находится вне магнитного поля, как это и задано конвенцией. Таким образом, символика типа (1. 1) меняется.
Перейдем к обычному n →. Выберем направление к контуру квадрата по отношению к нам, используя правило правого винта. Для всех элементов поверхности, заключенных в квадратный контур рамки, мы видим, что угол между нормалью n→ и вектором b→ равен π. Поток типа записи через поверхность рамки на расстоянии x от проволоки принимает вид
dφ= -b d s = -b -a -d x = — µ 02πil d x x (1. 3), величина индукции магнитного поля в бесконечном канале с током силы составляет
(1. 3) для нахождения общего требуемого расхода выглядит следующим образом
φ1 = ∫s -m 0 2 p i l d x = -m 0 2 p il∫bb + a d x x = -m 0 2 p i l -ln b + a b (1. 5).
Заменяет уравнение (1. 2) типа (1. 5). Работа, которую мы ищем, заключается в следующем
a = i ‘m 02πil -ln b + a B
Ответ: a = µ 0 2 p i i ‘l -ln b + a b.
Найдите силу, приложенную к коробке из предыдущего примера.
Чтобы найти желаемую силу, действующую на квадратную рамку с током в поле длинных проводов, предположим, что рамка смещена от магнитной силы на небольшое расстояние d x. Из этого следует, что сила совершает работу, равную
Элементарная работа D a может быть выражена следующим образом.
Давайте применим уравнения (2. 1) и (2. 2), чтобы проделать то же самое с силой. Мы принимаем: .
f d x = i ‘d → f = i’dφdx (2. 3).
Воспользуемся выражением, приведенным в примере 1.
dφ = — µ02πil d x→ dφdx = — µ 02πil x (2. 4).
(Заменим dφdx на (2. 3). У нас есть: i ‘m 02πil
f = i ‘m 02πil x (2. 5).
Каждый элемент контура квадратной рамки находится под воздействием силы (сила Амбера). В контексте мы видим, что действуют четыре силы и что стороны A B и D C равны по модулю и противоположны по направлению. Представление является формальным:.
Каждый элемент контура квадратной рамки находится под воздействием силы (сила Амбера). В контексте мы видим, что действуют четыре силы и что стороны A B и D C равны по модулю и противоположны по направлению. Представление является формальным:.
Поток магнитной индукции
Поток вектора магнитной индукции (или магнитный поток) (DF) в общем случае имеет следующий ступенчатый натуральный размер