Цепь прерывается, и конденсатор заряжается. В его катушке появляется тенденция. Когда клемма конденсатора соединена с внешним проводником, возникает сильный электрический разряд из-за низкого сопротивления канала. При высоких значениях ток эвакуации резко возрастает, и разряжаемая мощность также выше.
Колебательный контур
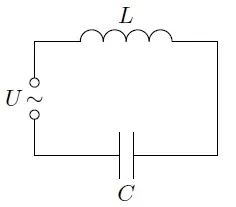
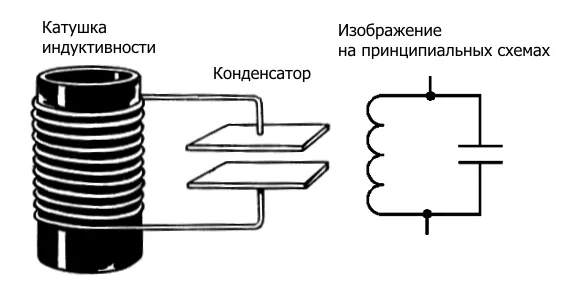
Колебательный контур представляет собой катушку, соединенную последовательно с замкнутым контуром, образованным конденсатором.
Конденсатор заряжается, и катушка подключается, чтобы замкнуть цепь. Начинают появляться свободные электромагнитные колебания — периодические изменения в конденсаторе и токе в катушке. Напомним, что колебания называются свободными из-за энергии, запасенной в контуре, и потому, что они протекают без какого-либо внешнего воздействия.
Как обычно, обозначим период колебаний контура. Сопротивление катушки считается равным нулю.
Давайте подробно рассмотрим все важные этапы процесса осцилляции. Для большей ясности мы будем пропорционально оценивать вибрацию пружины, движущейся горизонтально.
Первый импульс:. Конденсаторы одинаково заряжены, а ток в катушке отсутствует (рис. 1). Конденсатор начинает разряжаться.
Сопротивление катушки равно нулю, но ток увеличивается не сразу. Когда ток начинает увеличиваться, в катушке появляется самотормозящий ЭЭД, препятствующий увеличению тока.
Соотношение. Маятник притягивается вправо на определенную величину и отпускается в исходное мгновение. Начальная скорость маятника равна нулю.
Первый квартал периода:. Конденсатор разряжается, и в этот момент разряжается его нагрузка. Ток через катушку увеличивается (рис. 2).
Увеличение тока происходит постепенно. Электрическое поле в катушке препятствует увеличению тока и направлено на ток
Соотношение. Маятник движется влево и переходит в положение равновесия. Скорость маятника постепенно увеличивается. Деформация пружины (или другого регулируемого маятника) уменьшается.
Конец первого квартала:. Конденсатор полностью разгружен. Ток достиг своего максимального значения (рис. 3). Конденсатор начинает заряжаться.
Напряжение катушки сбрасывается, но ток исчезает не сразу. Когда ток начинает уменьшаться, в катушке появляется самоликвидирующийся HED, который предотвращает снижение мощности.
Соотношение. Маятник проходит через положение равновесия. Его скорость достигает максимальной цены. Пружина имеет нулевую деформацию.
Второй семестр :. Конденсатор перезаряжается — его катушка имеет нагрузку с противоположным знаком по сравнению с первым знаком (рис. 4).
Ток постепенно уменьшается. Электрическое вихревое поле катушки поддерживает уменьшение тока и совпадает с током.
Соотношение. Маятник продолжает двигаться влево — от положения равновесия до крайней точки справа. Его скорость постепенно уменьшается, а деформация пружины увеличивается.
Конец второго квартала. Конденсатор полностью заряжен, и его нагрузка снова равна (но с другой полярностью). Ток равен нулю (рис. 5). Теперь конденсатор начинает обратный заряд.

Соотношение. Маятник достиг своего правого конца. Ожидаемая скорость равна нулю. Напряжение пружины равно максимальному значению.
Третий квартал :. Началась вторая половина периода колебаний — процесс идет в обратном направлении. Конденсатор разряжается (рис. 6).
Энергетические превращения в колебательном контуре
Полагая, что сопротивление катушки равно нулю, продолжают исследовать незатухающие колебания контура. Конденсатор имеет емкость, а самопотенциал катушки равен.
Тепловые потери отсутствуют, поэтому энергия не уходит из контура. Он постоянно перераспределяется между конденсатором и катушкой.
Давайте немного порассуждаем о максимальной нагрузке на конденсатор и при отсутствии электричества. Энергия магнитного поля катушки в этой точке равна нулю. Вся энергия в цепи сосредоточена в конденсаторе.
Напротив, рассмотрим момент, когда ток равен максимуму и конденсатор разряжен. Энергия конденсатора равна нулю. Вся энергия цепи хранится в катушке: энергия катушки хранится в конденсаторе.
В любой момент времени, если нагрузка конденсатора равна, а катушка протекает под действием тока, энергия цепи равна.
Соотношение (1) применимо ко многим проблемам.
Электромеханические аналогии
В более ранней брошюре о самоиндукции основное внимание уделялось соотношению между индукцией и массой. Теперь мы можем определить некоторые взаимосвязи между электродинамикой и механическими размерами.
Аналогичная связь с (1) применима к ожидающей весне.
Здесь, как вы уже поняли, указана жесткость пружины, которая является отложенной массой, текущее значение координат и скорости маятника и его наивысшая цена.
Сравнивая уравнения (1) и (2) друг с другом, получается следующее соглашение
Из этих электромеханических пропорций можно сделать вывод о виде периода электромагнитного колебания в колебательном контуре.
На самом деле, как мы знаем, периоды колебаний отложенной пружины таковы.
Согласно пропорциям (5) и (6), здесь мы ставим массу на самовоспроизводство, а жесткость на обратную емкость. Мы принимаем:.
Электромеханические пропорции не нарушаются: тип (7) дает правильное уравнение для периода колебаний в вибрационной цепи. Он называется типом Томсона. Сразу же проводится более тщательный экспорт.
Разложение может быть положительным или отрицательным. В первом случае частота генератора должна быть выше частоты контура. В отрицательном случае должно быть выполнено еще одно условие. Частота генератора меньше частоты контура.
Собственная частота колебательного контура
Какова частота этих колебаний? Он зависит от параметров конденсатора и катушки и рассчитывается по типу Томпсона.
Тип Томпсона для расчета частоты колебательного контура. L — самопроизводительность катушки (GN), C — емкость конденсатора (F)
Добротность
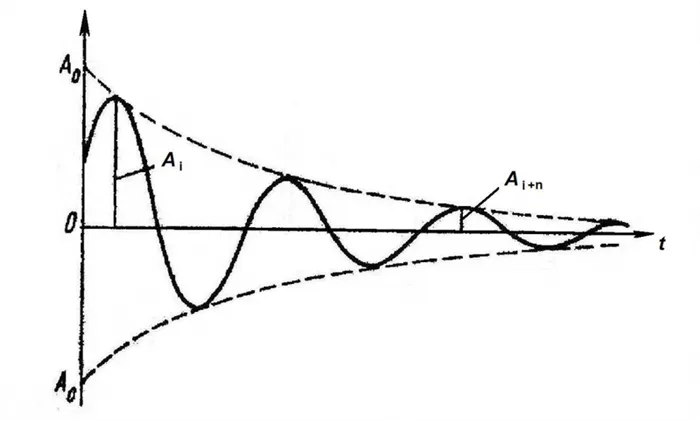
Но, конечно, эти колебания не могут продолжаться вечно. Как и в любой другой системе, существует сила сопротивления. Поэтому в каждом цикле часть энергии тратится на преодоление этого сопротивления, покидая систему в виде рассеянного тепла. Таким образом, без внешнего заряда электромагнитные колебания обесцениваются.
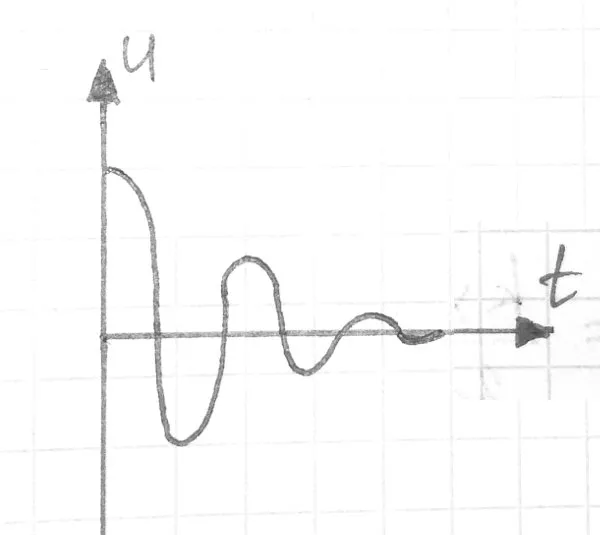
Ослабление колебаний. Зависимость ширины (u, вольт) от времени t
Иногда, чтобы четко обозначить наличие сопротивления в поворотной цепи, в нее добавляют «мнимое» сопротивление. Это отражает все потери в кабелях, конденсаторах и т.д.
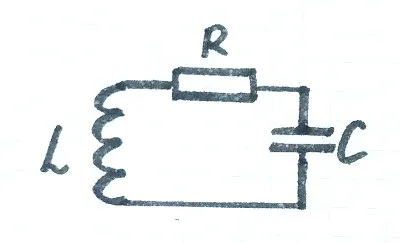
Чтобы выяснить, сколько энергии теряется в поворотной цепи, вводятся такие характеристики, как коэффициенты качества. Фактическое значение коэффициента качества — это отношение накопленной энергии к энергии, теряемой за цикл. Чем выше коэффициент качества, тем длиннее колебания. И это фактор качества человека:.

Чем выше самовоспроизводство l, тем ниже емкость крышки и тем выше коэффициент качества для данного типа. Нетрудно понять, почему это происходит. Дело в том, что в каждом цикле общая энергия системы разделяется на две части. Одна часть поглощается активным резистором R, а другая часть теряется накопителем (конденсатором или катушкой) или реактивными резисторами. Какая часть идет на что, зависит от соотношения этих резисторов. Другими словами, фактор качества является причиной снижения сопротивления.
Напомним, что в случае с катушкой реакция пропорциональна Я, а в случае с конденсатором она обратно пропорциональна емкости С.
Это интересный результат. Если необходимо увеличить коэффициент Q при сохранении частоты колебаний, необходимо увеличить L и уменьшить C на тот же коэффициент.
Механическая аналогия
Процессы в электрических цепях могут быть сложными для понимания. Это связано с тем, что все эти параметры — нагрузка, напряжение, ток и магнитное поле — являются в некоторой степени абстрактными. Поэтому мы используем аналогию с механическими системами, которые легко представить и поведение которых «очевидно» из нашего жизненного опыта. Другими словами, рассмотрим пружинный маятник.
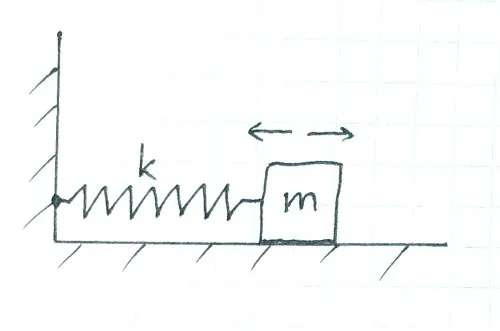
Весна приостановлена. k — коэффициент гибкости пружины, а m — масса груза
Пружина на удержании — это груз, прикрепленный к пружине, которая жестко закреплена на другом конце. Вес может скользить по гладким поверхностям. Если системе придать начальную энергию (например, путем сжатия пружины), она начинает свободно колебаться в равновесии. Это также описывается гармонизированными законами.
Пружина пропорциональна конденсатору. Конденсатор в цепи предотвращает изменение напряжения. Если напряжение увеличивается, конденсатор не допускает резких быстрых изменений напряжения. Конденсатор начинает относительно медленный процесс зарядки. Напротив, если внешнее напряжение падает, конденсатор стремится сохранить его на прежнем уровне, отдавая ему часть своей нагрузки.
Пружина также сопротивляется изменению своей длины. Когда она сжимается или разжимается, это всегда сопровождается накоплением энергии в пружине или, наоборот, высвобождением энергии (в зависимости от того, движется ли она к положению равновесия или нет).
Вес пропорционален индукционной катушке. Вес сопротивляется изменениям скорости так же, как индукционная катушка сопротивляется изменениям тока.
В свинг-системе всегда есть два энергетических склада. В нашем маятнике это динамическая энергия сжатой пружины и кинетическая энергия груза. Обмен энергией между ними вызывает колебания. Чтобы окончательно убедиться в соотношении между механическими и электромагнитными вибрациями, давайте сравним типы вибрации.
Частотный тип вибрационного контура (слева) в сравнении с пружинным маятником (справа)
Предполагая, что 1/k пропорционально C, мы видим, что типы полностью идентичны. Остается только один вопрос: почему 1/k пропорциональна C. Дело в том, что чем выше емкость конденсатора, тем «менее жестким» он является. Это означает, что для приведения грузового блока в движение требуется меньше работы. Энергия, запасенная в конденсаторе, обратно пропорциональна его емкости, а энергия пружины прямо пропорциональна ее упругости. Вот типы
Вид энергии в заряженном конденсаторе (слева) и энергии в сжатой пружине (справа)
Обратите внимание, что в обоих случаях частота не зависит от ширины. независимо от того, какое напряжение проходит через конденсатор, и независимо от степени сжатия пружины. Размер» или ширина колебаний зависит от количества энергии, поступающей в систему, в то время как частота остается постоянной.
Напротив, рассмотрим момент, когда ток равен максимуму и конденсатор разряжен. Энергия конденсатора равна нулю. Вся энергия цепи хранится в катушке: энергия катушки хранится в конденсаторе.
Резонанс LC-контура
Электромагнитные колебания в LC-контурах возникают на определенной частоте, называемой настройкой, подробнее о настройке. См. отдельную статью. Частота может изменяться путем изменения параметров схемы, таких как емкость капсюля, самовозбуждение катушки L, сопротивление резистора R (для схем LCR) и т.д.
Как рассчитать частоту регулировки вибрационного контура? Слишком легко! Вот окончательный вид:.
Применение колебательного контура
Вибрационные цепи широко используются на практике. Он является основой для изготовления частотных фильтров и необходим для всех радиоприемников и генераторов сигналов с определенными частотами.
Если вы не знаете, как рассчитать LC-контуры, или у вас мало времени, обратитесь в специализированный центр обслуживания студентов. Найдите быструю и качественную помощь для любой работы — быстро!
Как и в первом случае, параллельные идеальные колебательные контуры характеризуются индукцией и возможностью. Такая схема показана на рисунке.
Колебательный контур
Колебательный контур состоит из соединенных конденсатора и катушки.
Рисунок 1.Схема колебательного контура.
Цепь прерывается, и конденсатор заряжается. В его катушке появляется тенденция. Когда клемма конденсатора соединена с внешним проводником, возникает сильный электрический разряд из-за низкого сопротивления канала. При высоких значениях ток эвакуации резко возрастает, и разряжаемая мощность также выше.
Однако условия отличаются, когда цепь замыкается через катушку. Сопротивление катушки также низкое, но ток увеличивается не так сильно. То, что происходит дальше, состоит из двух этапов.
Первая стадия
Конденсатор начинает разряжаться через небольшое сопротивление катушки. Однако, благодаря явлению самоиндукции, магнитное поле, создаваемое катушкой, направлено таким образом, чтобы нейтрализовать его причину. Поэтому ток протекает гораздо медленнее, чем при коротком замыкании. После этого напряжение на конденсаторе падает. В результате максимальный ток не достигает значения короткого замыкания.
В конце фазы разрядки конденсатора ток, протекающий в цепи и обоих элементах, имеет максимальное значение, а напряжение на конденсаторе уменьшается до нуля.
Вторая стадия
И снова решающую роль играет феномен самоторговли. Поскольку напряжения на обоих элементах цепи равны нулю, ток должен прекратиться. Однако магнитный ток в индукционной катушке направлен таким образом, чтобы противодействовать этому. В результате ток не исчезает сразу, а уменьшается в течение некоторого времени.
Уменьшающийся ток проходит через разряженный конденсатор и заряжает его (уже в обратном направлении). Затем конденсатор снова заряжается, когда ток полностью уменьшается до нуля.

Рис. 2. Переход энергии в колебательный контур.
Формула Томсона
Чтобы выделить тип колебательного контура, следует отметить, что в контуре есть две формы действия.
Сумма этих величин равна $ w_c+w_c = const $. Теперь вы можете рассчитать скорость изменения каждого вида энергии (взяв производные по времени) и приравнять их для получения вида, после преобразования вы можете рассчитать частоту колебаний контура.
Или период колебаний:.
Этот тип называется типом Томсона по природе, которая его произвела.
Колебания в контуре
Из уравнения энергетического баланса цепи, зарядка конденсатора изменения нагрузки также может произойти.
Также может возникнуть уравнение тока в цепи, так как ток в цепи является производной груза по времени.
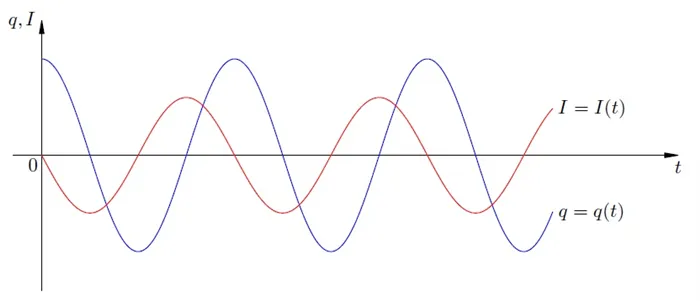
Из этих видов видно, что и колебания нагрузки, и колебания тока в цепи происходят по гармоническому закону, но они смещены друг относительно друга на четверть периода.

Рисунок 3.Кривые колебаний нагрузки и тока в цепи.
Схема качелей очень похожа на пружинную пружину. Нагрузка соответствует координатам, ток — мгновенной скорости, самовоспроизводство — массе, а мощность — мягкости пружины (большая мощность соответствует более мягкой пружине).
Схема имеет только активные резисторы, которые вызываются радиотехническими резисторами. Расчет по типу стойки = q * p. Если частота не равна регулируемой, то в схеме происходят другие процессы. Индуктивное сопротивление падает на более низких частотах, а емкостное сопротивление падает на более высоких частотах.
Период колебаний, от чего зависит
Периодичность свободных колебаний в колебательном контуре может быть определена с помощью типа Томпсона. Уравнение выглядит следующим образом.
- \(T\) T обозначает период колебаний и выражается в секундах;
- \(L\) — величина индуктивности, обозначается Гн (Генри);
- \(С\) используют для измерения электроемкости конденсатора, в Ф (Фарад);
- \(π\) – константа, равная 3,14.
Явление резонанса тока в колебательном контуре
Электромагнитные колебания в колебательных цепях характеризуются определенной частотой. Этот размер называется настройкой.

Частота вибрации зависит от различных параметров колебательного контура.
Типы частот вибрации, которые могут быть рассчитаны, следующие
Благодаря преобразованию различных видов энергии с помощью вибрационных контуров, они находят применение в различных областях электроэнергетики и машиностроения. Эти области изучаются студентами высших учебных заведений и специалистами и применяются в различных технических проектах. На портале Phoenix.help вы найдете быструю и компетентную помощь в ваших исследованиях.








