Кинетическая и потенциальная энергии. Как находить потенциальную энергию

Содержание

Одним из упругих свойств твердых тел или жидкостей при напряжении или деформации является то, что напряжение или деформация пропорциональны приложенной силе. Другими словами, для создания вдвое большей растягивающей силы требуется вдвое большая сила. Эта линейная зависимость смещения от приложенной мощности известна как закон Гука.

Потенциальная энергия

Потенциальная энергия ($ e_p $) взаимодействующих тел — это энергия, которая зависит от взаимного расположения этих тел. Консервативный проект силы ($ a $) равен изменению динамической энергии взаимодействующих систем организма.

Потенциальная энергия может быть рассчитана для любой константы. Если ко всем значениям динамической энергии добавить фиксированное значение, то получится новое значение динамической энергии. Это изменение динамической энергии не изменяет работу (1). Этот результат можно описать следующим образом. Нулевая динамическая энергия может быть выбрана произвольно. Если вы перейдете на другой нулевой уровень динамической энергии, значение динамической энергии изменится на одну и ту же величину во всех точках.

Говоря о потенциальной энергии тела, мы всегда должны четко представлять, где находится тело (с чем оно взаимодействует).

Потенциальная энергия разных видов потенциальных сил

Потенциальная энергия силы упругости выглядит следующим образом

где $ k $ — коэффициент гибкости пружины- $ \ дельта x $ — величина удлинения пружины. Если пружина не деформируется, то потенциальная энергия силы, действующей на шину, равна нулю (Lo_ delta x = 0). $.

Потенциальная энергия силы Кулона в системе СИ равна:.

где $q_1_2$ — точечные электрические заряды;

В физике наиболее важная форма называется механической энергией. Она представляет собой сумму и определение динамической и кинетической энергии и имеет вид: E = EK + WP.

[H1toH2]

Потенциальная энергия

Потенциальная энергия и потенциальная сила

В общем случае потенциальные силы, действующие на тело в данной точке динамического поля, и потенциальная энергия тела связаны с причиной

\ надпись = -GRADE_P = — \ слева (⌘ frac)<\partial E_p><\partial x>\ надстрочный + ⌘ фрагмент<\partial E_p><\partial y>\ надстрочный + ⌘ фрагмент<\partial E_p><\partial z>\ накладка \ справа) ߹ слева (߹ справа), ߹ где $ \ накладка, ߹ накладка, ߹ накладка $ — единичный вектор (орты). Если силовое поле обладает сферической симметрией, его можно преобразовать в уравнение (7).

Примеры задач с решением

Задание. Под действием силы $ f $ масса весом $ m = 10 $ кг поднята на высоту $ h = 10 $ м. Какова потенциальная мощность груза?

Решение. План.

Поскольку тело поднимается с Земли на высоту, намного меньшую, чем радиус Земли, используйте тип для расчета потенциальной энергии тела, поднятого Землей.

Примите поверхность Земли за нулевую потенциальную энергию. Ускорение свободного падения равно $ g = 9,8 \ {frac $:.

\ e_p = 10 \ cdot 9,8 \ cdot 10 = 980 \ слева (j \ справа). \ e_p = 10 \ cdot 9.8 cdot 10 = 980

Ответ. $ E_p = 980 $ J

Задание. Точка качества движется вдоль оси OX в положительном направлении оси в силовом поле, динамическая энергия которого показана графически (рис. 2). Как изменяются измерения ускорения для этой точки массы?

Решение. Динамическая энергия задается прямой линией (рис. 2), уравнение которой записывается в виде

где $ \ альфа =const$. Точка массы движется под действием позиционных сил, связанных с потенциальной энергией, в соответствии со следующим уравнением

Поскольку потенциальная энергия зависит только от координаты x, уравнение (2.2) имеет следующий вид

\ overline =- Ј frac \ overline \ left (2.3 \ right). \ надстрочный =- ˉˉˉˉ

Из уравнений (2.1) и (2.2) имеем

\࿌ overline =-{frac\ надпись =- 頻 альфа \ надпись \ слева (2,4 \ справа). \ \ \ слева (2.4)

где $ m$ — масса материала точки- $overline $ — ее ускорение, и

\ m \ overline =-Ј alpha \ overline \ to m \ left | a \ right | = \ alpha \ to \ left | a \ right | =Ј frac.

Ответ. Измеренное ускорение не изменяется.

Мы уже помогли 4 372 школьникам и студентам сдать на отлично письменные работы от решения задач до дипломной работы! Узнайте, сколько стоит ваша работа за 15 минут!

0$ — электрическая постоянная; $r$ — расстояние между зарядами. Потенциальная энергия приближается к нулю, если расстояние между зарядами увеличивается до бесконечности. Если оба взаимодействующих заряда обладают одинаковыми знаками, то они отталкиваются, при этом потенциальная энергия больше нуля. Если заряды имеют противоположные знаки, то они притягиваются, а потенциальная энергия их взаимодействия отрицательна.

Потенциальная энергия гравитации равна

где $ \gamma$ — гравитационная постоянная- $m_1;;m_2$ — масса материальной точки- $r$ — расстояние между точками. В этом случае потенциальная энергия отрицательна, поскольку гравитация является гравитационной. Если расстояние между массами бесконечно велико, то потенциальная энергия стремится к нулю.

Потенциальная энергия объекта, поднимающегося с поверхности Земли, равна

где $M$ — масса Земли- $R_Z$ — радиус Земли- $h$ — высота над поверхностью Земли, на которую поднимается тело- $m$ — масса тела. Если расстояние от поверхности Земли до этого тела мало ($ h \ ll R_Z $), то для расчета динамической энергии этого тела в поле Земли можно использовать приближенную формулу.

Единицей потенциальной энергии в Международной системе единиц является джоуль (Дж).

[/H1toH2]

В конечное мгновение происходит обратное. Кинетическая энергия равна нулю, потому что мяч больше не может лететь высоко, но потенциальная энергия максимальна, потому что мяч был брошен на максимальную высоту.

Теорема о кинетической энергии

Возвращаясь к рассмотренному примеру, сформулируем теорему для кинетической энергии объекта.

Теорема о кинетической энергии

Работа силы, приложенной к объекту, равна изменению кинетической энергии объекта. Это утверждение также верно, когда тело движется под действием силы, измерение и направление которой меняется.

Таким образом, кинетическая энергия объекта массы m, движущегося со скоростью v→, равна работе, которую должна совершить сила, чтобы разогнать объект до этой скорости.

Чтобы остановить организм, он должен совершить работу

Потенциальная энергия

Кинетическая энергия — это энергия движения. Помимо кинетической энергии, существует также динамическая энергия, то есть энергия взаимодействия между объектами. Это зависит от положения объектов.

Например, тело поднимается с земли. Чем выше подъем, тем больше потенциальная энергия. Эта сила действует, когда тело падает под действием силы тяжести. Тогда работа силы тяжести определяется только вертикальным движением тела и не зависит от его траектории.

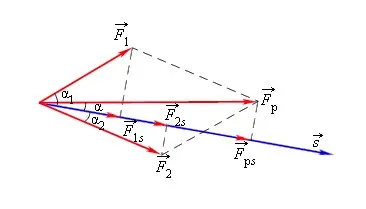
В общем, мы можем говорить о потенциальной энергии только в контексте сил, работа которых не зависит от формы орбиты тела. Такие силы называются консервативными.

Примеры сохраняющихся сил: гравитационные силы и силы упругости.

Когда объект движется вертикально вверх, гравитация действует отрицательно.

Рассмотрим пример шарика, перемещающегося из точки на высоте h1 в точку на высоте h2.

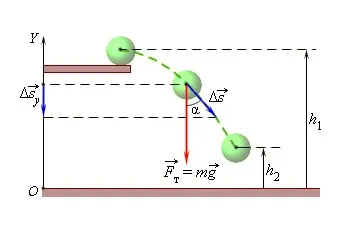
Таким образом, сила тяжести составляет

a = — m g (h 2 — h 1) = — (m g h 2 — m g h 1).

Эта работа равна изменению m g h с противоположным знаком.

Величина h = m g h — это потенциальная энергия гравитационного поля. В нулевой точке (на земле) потенциальная энергия тела равна нулю.

Значение. Потенциальная энергия.

Потенциальная энергия — это часть полной механической энергии системы в поле консервативных сил. Потенциальная энергия зависит от положения точек, составляющих систему.

Мы можем говорить о потенциальной энергии гравитационного поля, потенциальной энергии сжатой пружины и т.д.

Работа силы тяжести равна изменению динамической энергии с противоположными знаками.

Ясно, что потенциальная энергия зависит от выбора нулевого уровня (принцип координат оси OY). Подчеркните, что имеет смысл изменять потенциальную энергию по мере движения тела относительно других. При выборе нулевого уровня изменение динамической энергии будет таким же.

При расчете движения тела в гравитационном поле Земли, находящегося на значительном расстоянии от нее, необходимо учитывать общий закон гравитации (зависимость силы тяжести от расстояния от центра Земли). Это один из видов зависимости динамической энергии организма.

Здесь G — гравитационная постоянная, а M — масса Земли.

Потенциальная энергия пружины

В первом случае представим, что мы взяли пружину и удлинили ее на x. Во втором случае мы взяли пружину и удлинили ее на M. В последнем случае пружина сначала растягивается на 2 x, а затем сокращается на x. В обоих случаях пружина была удлинена на x. Это было сделано разными способами.

Работа силы упругости при изменении длины пружины на x одинакова в обоих случаях и составляет

Величина E U P = K X 2 2 называется динамической энергией пружины сжатия. Она равна работе упругих сил при переходе из определенного состояния тела в состояние с нулевой деформацией.

Для невращающихся частиц или твердых тел кинетическая энергия сбрасывается, когда тело останавливается. Однако для систем, содержащих много независимых частиц, это не совсем верно.

Потенциальная энергия в поле тяжести

Находясь в поле консервативных сил, тело обладает энергией, которая может быть потрачена на совершение работы (перемещение тела). Она называется потенциальной энергией и зависит только от образования системы, то есть от положения тела по отношению к источнику силы.

Рассмотрим движение тела в поле гравитации (которое является консервативным и центральным). Работа этой смены происходит по типу.

Если $ s достаточно мало, то гравитацию можно считать постоянной с определенной точностью. Если движение вертикальное, то $ s = h_2 -h_1 $. Если тело катится по наклонной поверхности, то смещение равно $ lcos \ varphi $. Однако этот продукт равен высоте, на которую опустилось тело. Это означает, что работа в поле гравитации определяется только исходным конечным положением тела. Поэтому:.

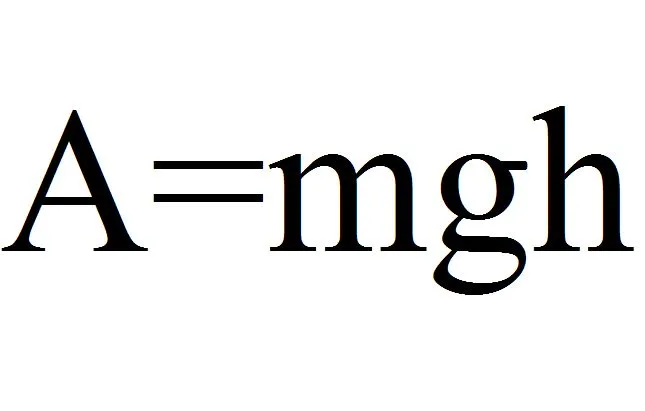
Рисунок 1.Гравитационные задачи.

Гравитационное произведение высоты называется потенциальной энергией тела в гравитационном поле. В этом случае $ MGH_1 $ принимается за потенциальную энергию нулевой точки.

Поскольку нулевая точка выбирается произвольно, значение динамической энергии в любой точке определяется ближайшей константой. Строго говоря, вид потенциальной энергии имеет вид $ v = mgh + c $.

В естественном смысле C равно нулю с точки зрения доли потенциальной энергии, сохраняемой телом. Учитывая различия между динамическими действиями в одной и той же точке нуля, константа уменьшается. Поэтому определение абсолютного значения динамической энергии в большинстве случаев не требуется.

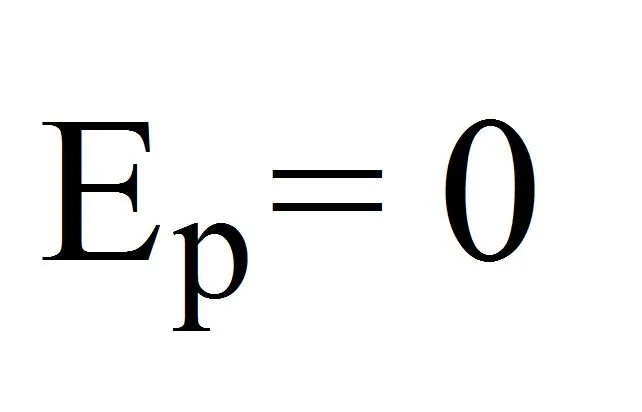
Рисунок 2.Потенциальная энергия в точке ноль.

Потенциальная энергия упругой деформации

Рассмотрите вопрос о затянувшейся весне. Точка x = 0 считается нулевой. Проект, необходимый для перемещения груза, связанного с грузом, определяется $ a = \ int_0^x kxdx = kx^$ 2 где kx — мощность упругости. В целом, произведение — это всегда законченный предмет. Выражение $ kx^$ 2 называется потенциальной энергией упругой деформации и зависит только от положения груза относительно нулевой точки и не зависит от периода изменения.

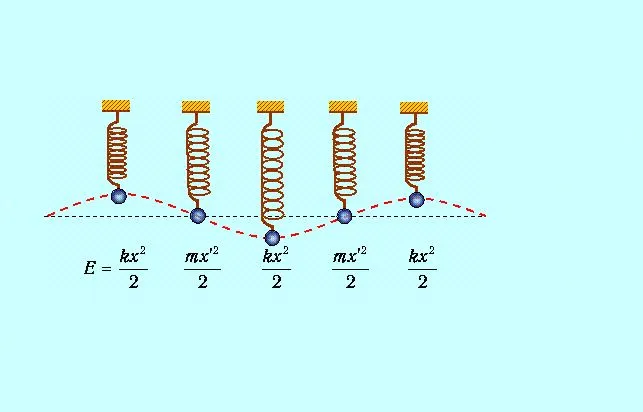
Рис. 3. Изменение энергии пружины.

В обоих случаях (работа в поле гравитации и вовлечение упругой деформации) есть одна общая черта. Если тело начинает движение с самого начала, то в конце концов оно возвращается к тому же принципу, и общая работа равна нулю.

Используя это правило, легко проверить, является ли власть консервативной или нет. Помимо уже упомянутых, к консервативным силам относятся также силы кулоновского взаимодействия.

Задачи

Альпинист массой 70 кг находится в штурмовом лагере, на высоте 5200 метров. Высота вершины – 6100. Найти его потенциальную энергию в каждой точке, приняв за нулевую точку уровень моря. Найти работу против силы тяжести, которую совершит альпинист, совершив переход от штурмового лагеря до вершины.

Решение первой проблемы.

При нулевом значении динамическая энергия считается равной нулю. Тогда в лагере атаки потенциальная энергия альпиниста в соответствующей нулевой точке равна.

$ v_1 = mgh_1 = 70g5200 = 3640 kj $

$ v_2 = mgh_2 = 70g6100 = 4270 kj $

Этот проект равен разнице между минимальной динамической энергией и максимальной.

$ a = mgh_2 -mgh_1 = 4270-3640 = 630 кдж $

Деформация пружины маятника равна 5 см, жесткость пружины равна 100 Н/м. Найти потенциальную энергию груза в момент, когда деформация максимальная.

Решение второй задачи.

Предполагая, что динамическая энергия в точке x = 0 равна нулю, напишите.

$ v = kx^2 = \ более 2> = 0,125 j $ — потенциальная энергия в точке максимальной деформации.

Следует отметить, что значение динамической энергии пружины всегда будет положительным, так как тип включает в себя изменения площади. В любом случае потенциальная энергия остается положительной, даже если на изменении стоит знак «-«.

Переход механической энергии во внутреннюю

Внутренняя энергия представляет собой сумму кинетической энергии хаотического теплового переноса молекул и динамической энергии их взаимодействия. Это энергия, запасенная в организме для его собственных параметров.

Во многих случаях механическая энергия преобразуется во внутреннюю энергию. Этот процесс осуществляется за счет механической работы организма. Например, когда проволока сгибается и разворачивается, она нагревается.

В другом случае, если мяч бросить о стену, часть энергии удара преобразуется во внутреннюю энергию.

Какая часть начальной кинетической энергии при ударе мяча о стену превращается во внутреннюю энергию, если начальная полная механическая энергия в итоге удваивается?

Первоначально мяч обладает только кинетической энергией._Мех. =é_Плата..

Наконец, механическая энергия составляет половину первоначальной энергии. Другими словами._Мех./2 =é_Плата./2

Поскольку часть энергии преобразуется во внутреннюю энергию, e_{Полностью.} =é_Мех./2 +é_{Интерьер.}

Ответ: половина начальной кинетической энергии передается внутрь помещения

Закон сохранения энергии в тепловых процессах

Для формулирования закона о поддержании энергии в тепловых процессах были предприняты два важных шага. Во-первых, французский математик и физик Жан-Батист Фурье установил один из фундаментальных законов тепловой терапии. Затем Сэнди Карн обнаружил, что тепловую энергию можно преобразовать в механическую.

Это был Фурье:.

По мере прохождения тепла через теплое тело, температура тела постепенно становится одинаковой и одинаковой в обоих телах — наступает состояние термодинамического равновесия.

Таким образом, первым важным открытием стал вывод о том, что все тепловые процессы, происходящие без участия внешних сил, необратимы.

Далее Карнаух обнаружил, что тепловая энергия нагретого объекта не может быть непосредственно преобразована в механическую энергию для производства работы. Это можно сделать только путем передачи части тепловой энергии одного горячего объекта другому объекту с более низкой температурой и нагревания его до более высокой температуры.

Закон сохранения энергии в тепловых процессах

При теплообмене между двумя или более объектами абсолютное количество тепла, выделяемого наиболее нагретым объектом, равно количеству тепла, получаемого наименее нагретым объектом.

Математику можно объяснить следующим образом

Уравнение теплового баланса

Q_{отключен} количество тепла J

Q_пол количество тепла J

Это уравнение называется уравнением теплового баланса. Реальные эксперименты показали, что количество тепла, выделяемого теплым телом, обычно больше, чем количество тепла, получаемого наименее горячим телом.

Это происходит потому, что часть теплообмена передается окружающему воздуху, а другая часть — контейнеру, в котором происходит теплообмен.

Чтобы понять суть проблемы, прочитайте статью о кумулятивном состоянии материи.

Проблема 1.

Учитывая, что 20% потребляемой энергии расходуется на нагревание, определите количество граммов спирта, которое необходимо сжечь в спиртовке для нагревания воды массой 580 г при температуре 80 °C.

Удельная теплота спирта составляет 2,9-10.₇ Дж/кг, в то время как удельная теплоемкость воды составляет 4200 Дж/(кг-°C).

При нагревании тело получает такое количество тепла

где c — удельная теплоемкость вещества.

При сгорании тела высвобождается энергия

где q — удельная теплота.

Согласно описанию вопроса, 20% энергии, используемой для сжигания спирта, используется для нагрева воды.

ОТВЕТ: масса сгоревшего топлива равна 33,6 г.

Второй вопрос.

-Какое минимальное количество тепла необходимо для превращения 500 г льда, полученного при температуре 10°C, в воду? Не учитывайте потери энергии на нагрев окружающего воздуха. Удельная теплота льда составляет 2100 Дж/кг-°C, а удельная температура плавления льда — 3,3-10 5 Дж/кг.

Чтобы нагреть лед при температуре его плавления, требуется

Q_{отопление} = 2100-0.5-(10-0) = 10500 J

Чтобы превратить лед в воду:.

Q_pl = 3.3-10 5-0.5 = 165 000 J

Поэтому вам необходимо потратить на трансформацию:.

Q = Q_{отопление} + Q_pl = 10500 + 165 000 = 175500 Дж = 175,5 кДж

ОТВЕТ: 175,5 кДж тепла требуется для превращения 0,5 кг льда в воду при данных условиях.