Перемещения и траектории равномерно ускоренного линейного движения изменяются так же, как и координаты тела. Поэтому их графики, зависящие от времени, также похожи на притчу.
Ускорение при равноускоренном прямолинейном движении
Ускорение тела равно отношению изменения вектора скорости к времени, в течение которого происходит это изменение.
v — скорость тела в этот момент времени. v0 — это скорость объекта в начальный момент времени, а t — время, в течение которого скорость изменилась.
Пример 1. Поезд движется и достигает скорости 36 км/ч за 20 секунд. Найдите ускорение этого ускорения.
Во-первых, договоритесь о единицах измерения. Для этого переведем скорость в м/с. Умножьте километры на 1000 и разделите на 3600 (в часе содержится большое количество секунд). Результат — 10 м/с.
Начальная скорость поезда равна 0 м/с, так как изначально поезд был неподвижен. Получив все данные, вы можете подставить их в формулу, чтобы найти ускорение
Проекция ускорения
vвату проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, а t — время, в течение которого скорость изменилась.
Знак проекции ускорения зависит от направления, в котором вектор ускорения направлен относительно оси OX.
- Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
- Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.
При решении задачи равномерно ускоряющегося линейного движения проекция величины может быть записана без нижнего указателя, так как при движении объекта по прямой его положение изменяется относительно единственной оси (OX). Если движение описывается более чем одной осью, они должны быть записаны.
Направление вектора ускорения
Направление вектора ускорения не всегда совпадает с направлением вектора скорости.
Равномерно ускоряющееся движение — это движение, при котором скорость изменяется на одну и ту же величину за один и тот же промежуток времени. В этом случае направление векторов скорости и ускорения совпадают (↑↑v).
Равномерно замедляющееся движение — это частный случай равномерно ускоряющегося движения, при котором скорость за один и тот же промежуток времени уменьшается на одну и ту же величину. Направления векторов скорости и ускорения противоположны друг другу (a. ↓v).
Пример 2. Автомобиль сначала разгоняется, а затем замедляется. Во время ускорения скорость и скорость вектора ускорения совпадают, так как скорость увеличивается. Однако при торможении скорость уменьшается, поскольку направление вектора ускорения меняется на противоположное.
Если величина скорости увеличивается с течением времени, то тангенциальное ускорение направлено в ту же сторону, что и скорость. Такое движение называется ускоренным.
Радиус-вектор и траектория точки
Рассмотрим движение точки массы M. Выберите фиксированную декартову систему координат Oxyz с центром в неподвижной точке O. Тогда положение точки M однозначно определяется ее координатами (x, y, z). Эти координаты являются компонентами радиус-вектора точки массы.
Радиус-вектор точки M — это вектор, проведенный из начальной точки неподвижной системы координат O точки M. где — единичный вектор в направлении осей x, y и z.
При перемещении точек их координаты изменяются во времени. Другими словами, они являются функцией времени. Тогда одновременные уравнения (1) можно рассматривать как уравнения кривой, заданной параметрическими уравнениями. Эта кривая является траекторией точки.
Траектория точки массы — это линия, по которой движется точка.
Если точки движутся в плоскости, оси и система координат могут быть выбраны так, чтобы они лежали в этой плоскости. Орбиты определяются двумя уравнениями, и в некоторых случаях время может быть исключено из этих уравнений. В таких случаях уравнения орбиты зависят от следующего вида где — функция. Эта зависимость включает переменные и. Параметры не включены.
Скорость материальной точки
Согласно определению скорости и производных: в технике производные по времени обозначаются символом «точка над». Здесь замените выражение для радиус-вектора. Здесь в явном виде показана зависимость координат от времени. Здесь 、、、、 — проекции скоростей на координатные оси. Они возникают в результате изменения во времени компонентов радиус-вектора.
Итак Модуль скорости:.
Касательная к траектории
С математической точки зрения одновременные уравнения (1) можно рассматривать как уравнения прямой линии (кривой), заданной параметрическими уравнениями. В этом представлении время играет роль параметра. Однако это компоненты вектора скорости точки. Это означает, что скорость точки массы направлена вдоль касательной к ее траектории.
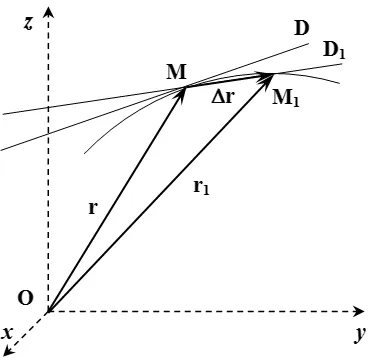
Все это можно доказать немедленно. Предположим, что в данный момент времени точка находится в положении радиус-вектора (см. схему). В данный момент она находится в положении радиус-вектора. Проведите прямую через точку и точку. По умолчанию, касательная линия — это линия, касательная к Ввести символизм: ? ;;. Далее, векторы, направленные по касательной к.
При касательных линия является касательной, а вектор — скоростью в определенный момент времени. Поскольку векторы ориентированы вдоль прямых и линий, векторы скорости ориентированы вдоль касательных. Другими словами, вектор скорости точки массы ориентирован вдоль касательной линии траектории.
Введем тангенциально ориентированный вектор единичной длины. Покажем, что длина этого вектора равна единицам. Действительно, поскольку:.
Здесь, для большего удобства, мы ориентировали вектор в направлении вектора скорости. Однако точка может остановиться и двигаться в обратном направлении по одной и той же орбите. Чтобы не вводить два единичных касательных вектора к одной и той же точке траектории, необходимо предусмотреть случай, когда направление противоположно скорости. Для этого вводится алгебраическое значение скорости. Если направления векторов совпадают. Если они противоположны,. — это проекция скорости на направление единичного вектора. Равно внутреннему произведению этих векторов:.
Абсолютный размер (модуль) вектора скорости представлен символом прямой скобки или символом без стрелки. Алгебраический размер вектора скорости:.
Вектор скорости точки может быть выражен следующим образом.
Ускорение материальной точки
Компонент ускорения (вид ускорения координатных осей), как и в предыдущем случае. ; ;. Измерение ускорения:.
Тангенциальное (касательное) и нормальное ускорения
Теперь рассмотрим направление вектора ускорения относительно траектории. Для этого примените следующее уравнение Примените правила дифференциации продукта для дифференциации во времени.
Вектор ориентирован вдоль касательной к траектории. В каком направлении движется производная по отношению к моменту времени?
Чтобы ответить на этот вопрос, воспользуемся тем, что длина вектора постоянна и равна единице. В этом случае квадрат его длины также равен единице. В дальнейшем два вектора в скобках — это их ступенчатые произведения. Выделим последнее уравнение во времени: ? ; ;. Произведение градиентов этих векторов равно нулю, поэтому эти векторы перпендикулярны друг другу. Поскольку векторы ориентированы вдоль касательной к траектории, векторы перпендикулярны касательной.
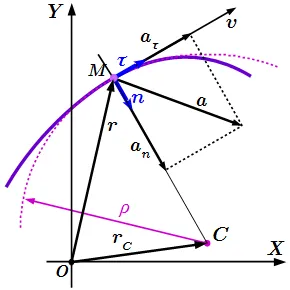
Скорость, тангенциальное и нормальное ускорение в точке M.
Первый компонент называется тангенциальным или касательным ускорением. Второй компонент называется нормальным ускорением. Далее, общее ускорение:. Это уравнение представляет собой анализ ускорения двух компонентов, перпендикулярных орбите и перпендикулярных друг другу.
Тангенциальное (касательное) ускорение
Для скорости введите алгебраическое значение вектора тангенциального ускорения. Если векторы тангенциального ускорения направлены в ту же сторону, что и случае эти векторы противоположны. Абсолютное значение тангенциального ускорения обозначено прямыми скобками. Итак
Умножьте обе части уравнения (2) на градусы. В конечном итоге Итак ;. Место здесь:. Таким образом, мы видим, что алгебраическое значение тангенциального ускорения равно проекции полного ускорения на тангенциальное направление траектории. Это также равно производной по времени от алгебраического значения скорости точки.
Заменив эти два показателя, мы получим, что Мы учтем это здесь.
Найдите производную по времени от коэффициента скорости. Примените правило дифференциации:? .
Да Если угол между вектором ускорения и вектором скорости составляет острый угол, то движение ускоряется. Абсолютное значение скорости увеличивается. Если угол между ними тупой:, движение замедляется. Абсолютное значение скорости уменьшается.
Выразите ускорение через тангенс и нормаль:, и оно дано. Получить:. Первое может быть выражено в терминах тангенциального ускорения. Если тангенциальное ускорение и вектор скорости направлены в одну сторону, то движение ускоряется. Если они расположены в противоположных направлениях, движение замедляется.
Радиус кривизны траектории
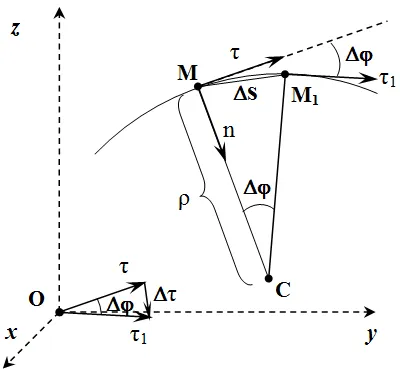
Рассмотрим векторы в двух точках в момент времени t и в момент времени t.1. Представьте символизм:. Согласно определению деривативов:. Предположим, что в момент времени t точка находится в положении M, а в момент времени t:.1 -позиция M1 (см. схему).
Значение ускорения определяется с учетом векторных свойств физической величины. В связи с ин. Мужчина. Единицей измерения ускорения являются метры/секунду в квадрате.
Мгновенное ускорение.
Мгновенное ускорение объекта (точки массы) в данный момент времени — это физическая величина, равная пределу, в котором среднее ускорение стремится к нулю. Другими словами, это ускорение, с которым объект развивается в течение очень долгого времени Время. Короткий период времени:.
Ускорение происходит в том же направлении, что и изменение скорости ΔX, изменение скорости в направлении изменения скорости ∆XY, изменение скорости в направлении изменения скорости ∆XZ).
При ускоренном линейном движении скорость объекта увеличивается по модулю. Это означает, что v2 > v1вектор ускорения имеет то же направление, что и вектор скорости2(v > v).
Если скорость объекта по модулю (v2 < v1), вектор ускорения имеет противоположное направление вектору скорости 2. Другими словами, в данном случае мы наблюдаем замедление движения (ускорение отрицательное и< 0). На рисунке ниже изображено направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.
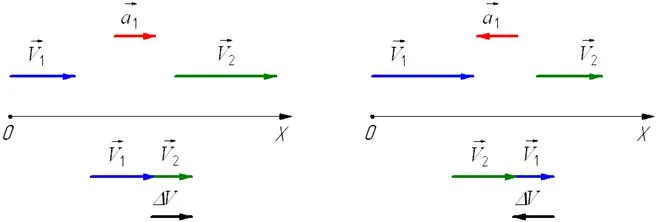
Если происходит движение по изогнутому пути, измеренные скорость и направление изменятся. Это означает, что вектор ускорения представлен в виде двух компонентов.
Тангенциальное ускорение.
Тангенциальное ускорение — это компонент вектора ускорения, направленный по касательной к треку в определенной точке трека. Тангенциальное ускорение представляет собой степень изменения скорости при криволинейном движении.
Вектор тангенциального ускорения t (см. выше) находится в том же направлении, что и линейная скорость, или наоборот. Это означает, что вектор тангенциального ускорения лежит на той же оси, что и орбита тела, — касательной окружности.
Нормальное ускорение.
Нормальное ускорение — это часть вектора ускорений, направленная перпендикулярно траектории движения в конкретной точке траектории тела. Другими словами, вектор нормального ускорения перпендикулярен линейной скорости движения (см. схему выше). Нормальное ускорение представляет собой степень изменения скорости в данном направлении и обозначается n.n. Вектор нормального ускорения направлен вдоль радиуса кривизны дорожки.
Полное ускорение криволинейного движения складывается из тангенциального и нормального ускорений по правилу сложения векторов и рассчитывается по следующему уравнению.
(Пифагорейская теорема для прямоугольников). Используя правило сложения векторов, вычисляется также направление суммарного ускорения
где α — ускорение тела м / с 2, V — мгновенная скорость м / с, V0 — начальная скорость м/с, а t — время с.
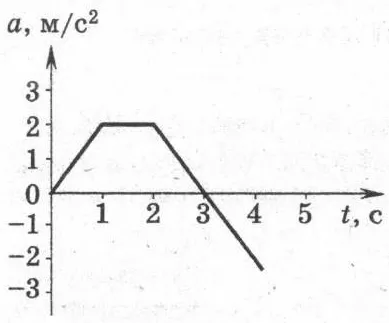
п.4. Определение пути и перемещения по графику скорости
В § 10 данного пособия было рассмотрено нерегулярное линейное движение. Это может быть разделено на отдельные, однородные секции. Для таких движений путь равен сумме коэффициентов участков, определенных на графике скорости. Смещение также будет равно сумме поверхностей, но при этом учитывается знак. Этот подход может быть распространен на любое поточное движение.
Предположим, что график скорости линейного движения разбит на ዄ (n \) сегментов, площадь которых можно легко определить (треугольники, прямоугольники, таблицы). Тогда: общее пройденное расстояние равно сумме коэффициентов площадей всех отрезков: $ s = | s_1 | + | s_2|+. + | s_n | Величина смещения вдоль оси OX равна сумме площадей всех сегментов с учетом следующего знака. $\ треугольник x= s_1 +s_2+. s_n $Окончательные координаты: ǫ(x_k = x_0 + ǫ-треугольник xǫ)
Пример определения путей и перемещений из графика скоростейДля графика скоростей, построенного выше, получены следующие участки:1) ΔABE, площадь которого равна $ s_1 = \ frac12 AE \ cdot BE = \ frac12 \ cdot 5 \ cdot 20 = 50 \(м)$ 2) прямоугольник EBCF, площадь которого равна $ s_2 = = EF \ cdot BE = 10 \ cdot 20 = 200 \ (м)$ 3) ΔCFD, площадь которого равна $ s_2 = \ frac12 FD \ cdot GF = \ frac12 \ cdot 4 \ cdot 20 = 40 \ (м)$ Все расстояния: $ s = s_1 + s_2 + s_3 = 50 + 200 + 40 = 290 \ (м). ) $Скорость автомобиля всегда оставалась положительной (потому что направление движения не менялось), а пройденный объем равен пройденному расстоянию. $\ треугольник х = с = 290 \(м)$.
п.5. Задачи
Задача 1.За 1 минуту скорость автобуса увеличилась с 28,8 км/ч до 72 км/ч. Найдите его ускорение и изобразите графически зависимость между скоростью и временем.
Дано:Ў(t = 1 \ мин = 60 \ с \)Ў(v_0 = 28,8 \ км/ч = 8 \ м/с \)Ў(v = 72 \ км/ч = 20 \ м/с \)__________________ \(a-? (\) Как перевести км/ч в м/с — см. §7 данного руководства.
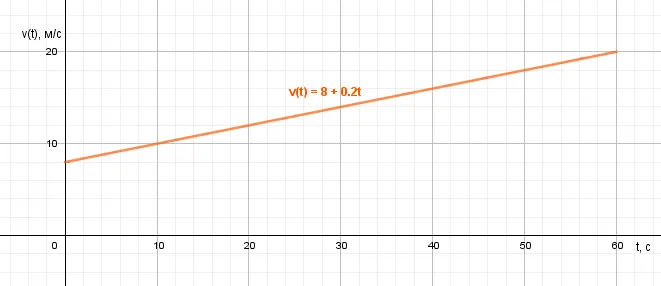
Поверните вал КРС в направлении движения автобуса. Автобус не меняет направления движения, проекции ускорения и скорости всегда положительны и равны по цене и величине. $ a = \ frac = 0.2 \ слева (⌘ frac \ справа)$ Уравнение времени удалено Время: ⌘ begin v(t) = v_0+at \ v(t) = 8+0.2t \ end график: reply: reply: 0.2 м/с 2
Вопрос 2. Один поезд двигался по ровной прямой линии со скоростью 18 км/ч. Во время торможения он ускорился и остановился через 10 с. Найдите коэффициент ускорения. Постройте график зависимости между скоростью и ускорением и найдите расстояние, пройденное поездом за все время.
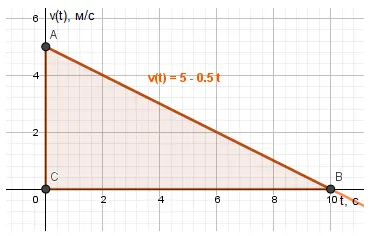
Укажите: \(v_0 = 18 \ км/ч = 5 \ м/с \)\(v = 0 \)\(t = 10 \ с \)__________________ \(a, \ с-? \ˉ) Повернем вал коровы в направлении скорости ˉ (v_0 \). Тогда проекция ускорения: $ a_x = \ frac, ˈ \ a_x = \ frac = -0.5 \ (м/с^2)$ Проекция при замедлении отрицательна. Величина ускорения (модуль): $ a = | a_x | = 0.5 \ м/с^2 $ Зависимость от скорости: ⌘ begin v(t) = v_0+a_x t \ v(t) = 5- 0.5t \ end График: пройденное расстояние равно площади треугольника DABC: $ s = \ frac12 ac \ cdot bc = \ frac12 \ cdot 5 \ cdot 10 = 25 \ (м) $ $: 0,5 м/с 2; 25 м
Вопрос 3*. С каким ускорением двигался автомобиль, если его скорость увеличилась с 36 км/ч до 72 км/ч на пути 600 м? Постройте график зависимости скорости от времени и используйте график для нахождения времени в пути и маршрута, а также проверьте полученные значения маршрута.
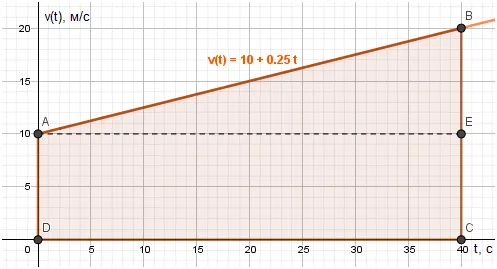
Укажите: Ј(v_0 = 36 \ км/ч = 10 \ м/с \)Ј(v = 72 \ км/ч = 20 \ м/с \)Ј(s = 600 \ м \)__________________ \(a-?, Ј t-? \ዄ) ускорение равно: ዄ(a = \ frac \). Один момент равен следующему моменту: \(t = \ frac \) Средняя скорость в течение: \(v = \ frac \) Всего времени: $ s = \ frac \ cdot \ frac = \ frac $ поэтому ускорение равно. Замена $ a = \ frac $: $ a = \ frac = 0,25 \ слева (\ frac \ справа) $ v(t) = 10+0,25t \ конечный график: скорость достигает значения Ў (v = 20 \ м/с \) в момент времени \ (t = 40 \ с \). Это означает, что время в пути составляет 40 секунд.
Корень из графика скорости равен площади четырехугольника ABCD. \ begin s_ = s_+s _ = \ frac12 ae \ cdot eb+ae \ cdot ad = \ frac12 \ cdot 40 \ cdot 10+40 \ cdot 10 = 200+400 = 600 \ (m)ޣ s = 600 \ m \ ends цена найденного маршрута соответствует рассматриваемому договору. Все параметры движения были найдены правильно. Ответ: 0,25 м/с 2; 40 c
Шкипер подошел к холму на высоте 36 м со скоростью 3 м/с и спустился за несколько секунд с конечной скоростью 15 м/с. Положение шкипера определяется через 2 с после начала движения от начала координат.
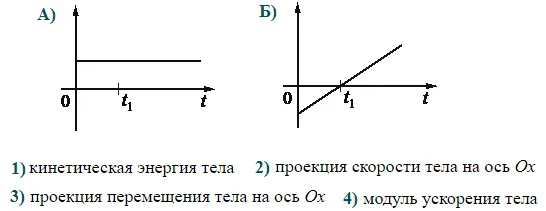
Графики равноускоренного движения
Математически, зависимость координат от времени в равноускоренном движении является функцией квадрата, а график — притчей.
Обратите внимание, что когда проекция скорости меняет знак, автомобиль поворачивается и движется в противоположном направлении.
Наша жизнь находится в движении, и онлайн-уроки физики на SkySmart помогут вам ускорить свой курс на покорение теорий и решение различных задач!








