Затем рисуется вид со смещением. Согласно этому уравнению, проекция смещения линейно зависит от времени. Поэтому его график является линейным, а направление и угол наклона относительно оси времени зависит от проекции вектора скорости на координатные оси.
Равномерное прямолинейное движение
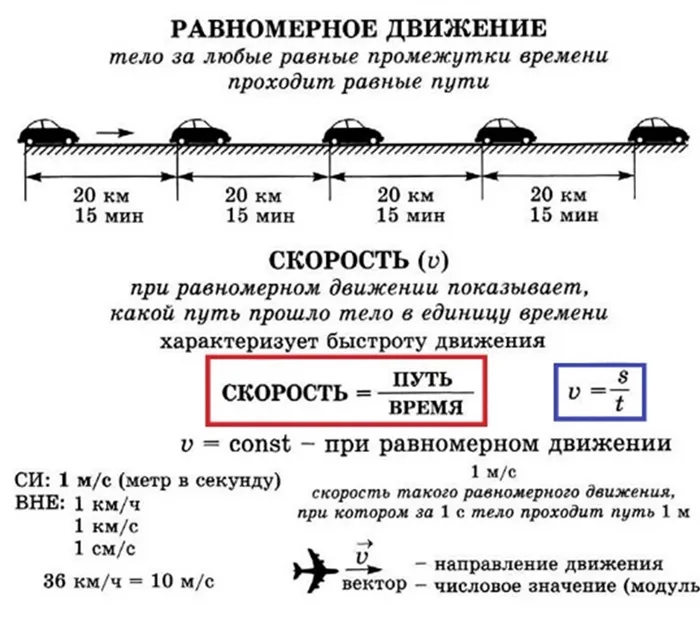
Равномерное прямолинейное движение — это движение, при котором тело движется равномерно за любой равный промежуток времени.
Если объект движется равномерно по прямой линии, его скорость остается постоянной как по измерению, так и по направлению. Ускорение в этом случае равно нулю.
Векторный способ записи скорости при равномерном прямолинейном движении: s — вектор перемещения, ΔR — изменение радиус-вектора, t — время, а ∆t — его изменение. Проекция скорости на ось ОХ: sЧаны. — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы). Знак модуля скорости зависит от направления вектора скорости и оси координат:
Основной единицей измерения скорости является 1 метр в секунду. Сокращенно она обозначается 1 м/с.
- 1 км/ч (километр в час) = 1000 м/3600 с.
- 1 км/мин (километр в минуту) = 1000 м/60 с.
- 1 км/с (километр в секунду) = 1000 м/с.
- 1 м/мин (метр в минуту) = 1 м/60 с.
- 1 см/с (сантиметр в секунду) = 0,01 м/с.
Спидометр — это устройство для измерения скорости движения тела.
График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Это происходит следующим образом.
- Если график скорости лежит выше оси времени, тело движется в направлении оси ОХ.
- Если график скорости лежит ниже оси времени, тело движется против оси ОХ.
- Если график скорости совпадает с осью времени, тело покоится.
Чтобы сравнить молекулы скорости на графике, необходимо оценить расстояние до оси времени. Чем дальше график находится от оси времени, тем больше показатель.
Пример 1.Найдите меру скорости и направления движения объекта относительно оси Ох. Выразите скорость в км/ч.
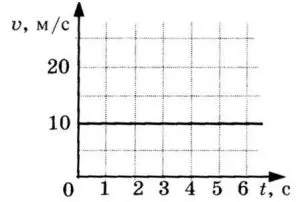
Диаграмма скоростей пересекает ось в точке со значением 10. Единица измерения — м/с. Таким образом, измеренное значение скорости равно 10 м/с. График лежит на оси времени. Это означает, что тело движется в направлении оси OX. Чтобы выразить скорость в км/ч, необходимо перевести 10 м в километры и 1 секунду в часы.
Затем разделите километры на время.
Перемещение и координаты тела при равномерном прямолинейном движении
Геометрический смысл смещения заключается в том, что его измеренная величина равна площади фигуры, ограниченной графиком скорости, осями скорости и времени и линией, проведенной перпендикулярно оси времени.
При прямолинейном равномерном движении эта форма представляет собой прямоугольник. Таким образом, измерение смещения рассчитывается по следующему уравнению
Вектор перемещения равен произведению вектора скорости на время движения:
При равномерном линейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, может быть найден с помощью того же уравнения.
Уравнение для отображения сдвига:.
График проекции перемещения
График проекции смещения показывает зависимость этой проекции от времени. Для линейного равномерного движения он представляет собой радиус, исходящий из начальной точки координат. Это происходит следующим образом.
- Если луч лежит выше оси времени, тело движется в направлении оси ОХ.
- Если луч лежит ниже оси времени, тело движется против оси ОХ.
- Если луч совпадает с этой осью, тело покоится.
Для сравнения числителя скорости из графика проекции смещения необходимо сравнить угол наклона относительно оси sЧаны. Чем меньше угол, тем больше показатель эластичности. Согласно приведенной схеме, на рисунках 1 и 3 видно, что скорости соответствующих объектов равны. Они больше, чем показатели скорости тела 2 из-за большего угла с.Чаны. Маленький.
График координаты
Координатный график — это график зависимости между координатами и временем. Он заключается в следующем.
Так как координатный график является графиком линейной функции, то координатное уравнение становится
- Если с течением времени координата увеличивается (график идет снизу вверх), тело движется в направлении оси ОХ. На картинке выше этому соответствуют графики тел 1 и 2.
- Если с течением времени координата уменьшается (график идет сверху вниз), тело движется противоположно направлению оси ОХ. На картинке выше этому соответствует график тела 3.
- Если координата не изменяется, тело покоится.
Чтобы сравнить числитель скорости объекта на координатном графике, необходимо сравнить угол наклона графика с координатной осью. Чем меньше угол, тем больше скорость. На приведенной выше диаграмме наибольший коэффициент скорости соответствует графику 1. В формах сигнала 2 и 3 коэффициенты равны.
Чтобы найти время слияния двух объектов на графике, необходимо провести вертикальную линию из точки пересечения графиков на оси времени.
Пример №2. График зависимости координаты тела от времени имеет вид:
Изучите график и выберите два правильных утверждения на его основе.
- На участке 1 скорость тела постоянна, а на участке 2 равна нулю.
- Проекция ускорения тела на участке 1 положительна, а на участке 2 — отрицательна.
- На участке 1 тело движется равномерно, а на участке 2 оно покоится.
- На участке 1 тело движется равноускорено, а на участке 2 оно движется равномерно.
- Проекция ускорения тела на участке 1 отрицательна, а на участке 2 — положительна.
Ответ на этот вопрос зависит от типа движения, которое совершает тело. Сначала мы рассмотрим самый простой вид движения — равномерное прямолинейное движение.
Как записывается кинематический закон прямолинейного равномерного движения
Основная задача инженерии — указать положение тела в пространстве в любой момент времени. Это помогает предсказать положение тела в любой момент как в будущем, так и в настоящем. Законы движения способствуют достижению этой цели.
Законы движения — это математические формулировки, которые описывают, как движется тело. Это набор зависимостей, которые раскрывают данные о движении точечного материала.
Если в момент времени t тело движется равномерно по прямой линии вдоль оси кислоты, то уравнение имеет вид
Это уравнение вытекает из двух уравнений.
Если тело движется против положительного направления оси ˉ (o_x \), то проекция вала отрицательна, а скорость тела, как говорят, меньше нуля. Тогда уравнение принимает вид
Скорость при прямолинейном равномерном движении
Скорость движения (v) имеет величину, равную отношению перемещений тела за этот промежуток времени.
Другими словами, скорость движения тела показывает, насколько тело перемещается в единицу времени. Чем больше смещение за определенный период времени, тем выше скорость.
На прямой линии скорость остается постоянной с точки зрения измерения и направления. Ускорение равно нулю.
В СИ основной единицей измерения скорости является 1 метр в секунду.
Это аббревиатура для 1 м/с. Можно использовать дополнительные устройства.
- 1 км/ч = 1000 м/3600 с;
- 1 км/мин = 1000 м/60 с;
- 1 км/с = 1000 м/с;
- 1 м/мин = 1 м/60 с;
- 1 см/с = 0,01м/с.
Коэффициенты скорости измеряются с помощью измерителя скорости.
Основные формулы
Перемещение указывается в векторных единицах.
Скорость также указывается в векторных единицах. Это означает, что существует не только одно измерение, но и одно направление.
Время, с другой стороны, не указывается и имеет размер шага.
Из определения следует, что скорость теперь равна делению перемещения на время.
Запишите уравнение в векторной форме.
Если направление скорости и перемещения не имеет значения для решения задачи, векторы можно не указывать. Затем расчет по скорости и перемещению выполняется так же, как и для обычных пошаговых величин.
Создайте дополнительные типы.
Векторное перемещение, или пошаговая траектория движения, равна скорости во времени.
)
Время, необходимое телу со скоростью V для перемещения на расстояние s, равно
Примеры равномерного прямолинейного движения
Равномерное прямолинейное движение — почти неслыханное явление в жизни. Это идеализация, которая упрощает расчеты, используя свойства прямолинейного движения. Практически невозможно создать условия, при которых тело могло бы двигаться с одной и той же скоростью в течение длительного времени. Однако в идеальном мире реальные движения могут быть приближены к равномерному движению с некоторой степенью погрешности.
Наиболее близким к естественному равномерному движению является движение небесных тел в пространстве, где они взаимодействуют друг с другом, а влияние других сил можно игнорировать.
Есть примеры других движений, которые ближе к линейным.
- Автомобиль едет по прямой автомагистрали с постоянной скоростью.
- Человек или другое живое существо идет по прямой дороге с неизменной скоростью.
Наконец, существует график зависимости между координатами тела и временем. Это также называется графиком движения. Чтобы построить такой график, необходимо знать уравнения движения тела. Давайте составим такое уравнение для велосипедистов.
Равномерное прямолинейное движение

1. равномерное прямолинейное движение — движение, при котором равные промежутки времени тела движутся одинаково. Слово «произвольный» подразумевает, что тело совершает одно и то же движение каждый час, каждую минуту, каждые полчаса, каждую секунду, каждую секунду.
Равномерное движение — это идеализация. Это связано с тем, что практически невозможно создать условия, при которых движения тела были бы равномерными во времени. Фактическое движение может лишь приближаться к равномерному движению с разной степенью точности. 2.
2. изменение положения тела в пространстве при равномерном движении может происходить с разной скоростью. Эта характеристика движения, его «скорость», характеризуется его естественным размером, называемым скоростью.
Скорость равномерного линейного движения — это натуральная величина вектора, равная отношению смещения к времени, за которое произошло смещение.
Если тело движется ᢙ (t \) во времени, то скорость ᢙ (ᢙ vec \) равна ᢙ (ᢙ vec = ᢙ frac<\vec> (\frac).
Единицы измерения скорости: 슰 (슰, v \, = \ frac \); 슰 (슰, v, = \ frac = 1 \ frac \). Единицей измерения скорости является 1 м/с — это скорость равномерного движения, при которой тело перемещается на 1 м за 1 секунду.
Зная скорость равномерного движения, можно найти перемещение в любой момент времени: ɛ (ɛ vec = \ vect \). Вектор скорости и вектор перемещения направлены в ту же сторону, что и направление движения тела.
3. основной задачей инженерии является определение положения тела, т.е. его координированного состояния, в любой момент времени, поэтому уравнение координированной зависимости тела от времени при равномерном движении должно быть записано.
Тело заставляют меняться (рис. 11). Направьте ось координат ox в направлении смещения. Найдите величину смещения в направлении OX. На рисунке ⌘(x_0 \) — это координата начальной точки перемещения, а ⌘(x \) — координата конечной точки перемещения. Показание перемещения равно разности между координатами принципиальной точки и конца перемещения: ⌘(⌘ vec_x = x-x_0 \). С другой стороны, индикация перемещения равна проекции скорости на время: \(\ vec_x = \ vec_xt \). Отсюда \(x-x_0 = \ vec_xt \) или \(x = x_0+\ vec_xt \). Если начальные координаты\(x_0 \) = 0, то \(x = \ vec_xt \).
Этот тип позволяет определить координаты равномерно движущегося тела в любой момент времени при условии, что известны начальные координаты и проекция движения.
Проекция скорости может быть как положительной, так и отрицательной. Проекция скорости положительна, если направление движения совпадает с положительным направлением оси ОХ (рис. 12). В этом случае \( x>x_0 \) . Проекция скорости отрицательна, если тело движется против положительного направления оси ОХ (рис. 12). В этом случае \( x
4. скорректированная временная зависимость может быть представлена графически.
Предположим, что тело движется от начала координат вдоль положительного направления вала КРС с постоянной скоростью. Покажите, что скорость вала равна 4 м/с. Уравнение движения в этом случае имеет вид \(x) = 4 м/с — \(t \). Скорректированная временная зависимость является линейной. Эта зависимость проводится в виде прямой линии через первую (рис. 13).
ПРИМЕРЫ ЗАДАНИЙ
1. если показание сдвига на 4 с равно 80 м, какова расчетная скорость равномерно движущегося автомобиля?
1) 320 м/с 2) 80 м/с 3) 20 м/с 4) 0,05 м/с.
2. если лететь со скоростью 5 м/с, каково смещение маховика за 0,5 мин?
1) 0,25 м 2) 6 м 3) 10 м 4) 150 м
Автомобиль Renault преодолевает расстояние в 1,2 км за 1 минуту. Peugeot проехал 0,2 км за 20 секунд. Сравните скорости Renault ˉ (v_1 \) и Peugeot ˉ (v_2 \).
1) \(V_1 = V_2 \) 2) \(V_1 = 2V_2 \) 3) \(2V_1 = V_2 \) 4) \(1,2V_1 = 10V_2 \)
4.На рисунке изображена гистограмма. Он представляет собой маршрут, пройденный мухой (1) и воробьем (2) в равномерном движении. Скорости сравниваются с сопоставлениями\(v_1 \)и\(v_2 \).

1) \(V_1 = V_2 \) 2) \(V_1 = 2V_2 \) 3) \(3V_1 = V_2 \) 4) \(2V_1 = V_2 \)
5.На рисунке представлен график зависимости скорости равномерного движения от времени. Измерения движения в течение 2 с.
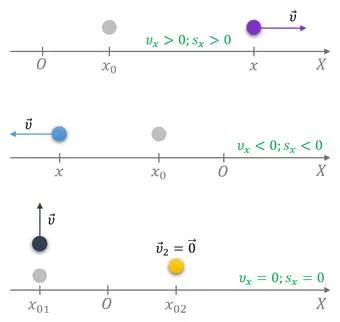
1) 20 м 2) 40 м 3) 80 м 4) 160 м
6.На диаграмме показано расстояние, которое проходит тело при равномерном движении, в зависимости от времени. Показателями скорости тела являются.
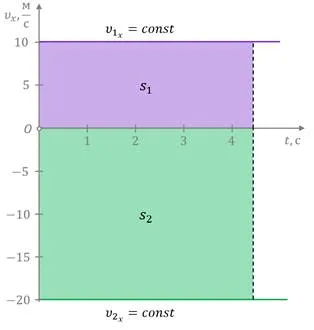
1) 0,1 м/с 2) 10 м/с 3) 20 м/с 4) 40 м/с.
7.На рисунке показан график зависимости времени трех тел от времени. Сравните значения скоростей ⌘(v_1 \), ⌘(v_2 \) и ⌘(v_3 \) этих движений тела.

1) \( v_1=v_2=v_3 \) 2) \( v_1>v_2>v_3 \) 3) \( v_1 4) \( v_1=v_2 \), \( v_3
8.Какой из следующих графиков отображает зависимость между маршрутом и временем при равномерном движении тела?
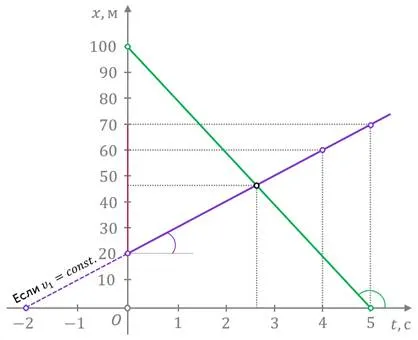
9.График координат времени тела показан на диаграмме. Каковы координаты тела в момент времени 6 секунд?

10.Уравнение движения объекта на графике в вопросе 9 имеет вид
1) Ј(x = 1t \) (m) 2) Ј(x = 2+3t \) (m) 3) Ј(x = 2-1t \) (m) 4) Ј(x = 4+2t \)
11. установите соответствие между величинами в левом столбце в соответствии со значением выбранной величины системы отсчета в правом столбце. В таблице под количеством когнитивных элементов в левой колонке напишите соответствующий номер выбранного элемента правой колонки.
Изменение a) перемещения b) времени c) скорости
Независимо от надежности 1) 2) в системе секций кафедры.
12 На рисунке вы видите график зависимости между координатами тела и временем. Какие выводы вы можете сделать на основе графического анализа? Даны два правильных ответа.

Скорость равномерного прямолинейного движения равна отношению пройденного расстояния к затраченному времени: $ v = \ frac st = const $ эта величина постоянна (константа).
п.5. Задачи
Вопрос 1: Если скорость реки равна 1,2 м/с, на какое расстояние она удалится от берега за 20 минут? Выразите расстояние в километрах.
Дано: t = 20 мин = 1200 с v = 1,2 м/с ______________________ с-?
Расстояние по прямой: s = vt Подставим: s =1,2∙1200= 1440 (м) = 1,44 (км) Ответ: 1,44 км
Вопрос 2. Выражается в метрах в секунду. Следующие значения скорости: 36 км/ч, 1,8 км/ч, 540 км/ч, 7,2 км/ч
Работа 3. Выразите следующие скорости в 10 км/ч: 10 м/с, 15 м/с, 25 м/с, 8 м/с.
Работа 4: Усэйн Болт, чемпион мира в беге на 100 м, пробежал дистанцию за 9,58 с. Если скорость ветра 6 м/с, можно ли сказать, что он бежит быстрее ветра? Какова скорость ураганного ветра при скорости 33 м/с? Сколько раз.
Скорость курсора ߡ (v = \ frac st \). \ (v = \ frac \ amptx 10.4 \ (ᢙ text) ᢙ gt v _> \) ᢙ (ᢙ frac)
Ответ: В 1,7 раза выше, чем при умеренном ветре. Это в 3,2 раза больше ураганного ветра.
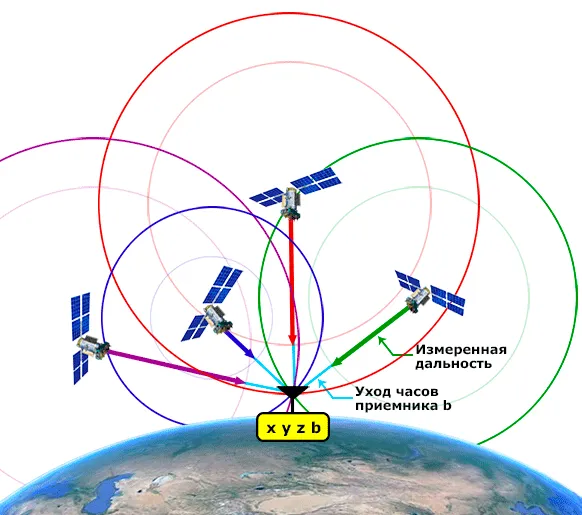
Вопрос 5.Во время сближения минимальное расстояние между Землей и Марсом составляет 55 миллионов километров. Если ответ придет вскоре после получения сигнала, сколько времени оператор потратит на Земле, чтобы получить ответ на запрос, отправленный на Марс по каналу связи? Скорость сигнала равна скорости света. Если планета находится на расстоянии более 404 миллионов километров, как долго вам придется ждать ответа?
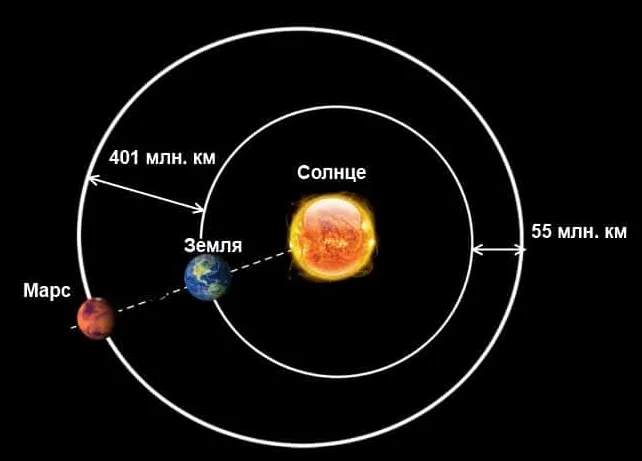
Дано: смин.= 55- 10 6 км = 55-10 9 м c = 3- 10 8 м/с sМакс.= 401- 10 6 км = 4.01-10 11 м __________________________
Сигнал посылается с Земли, переносится на Марс, и оттуда сразу же приходит ответ. Расстояние в обоих направлениях составляет 2 с. Требуемое время ожидания: ⌘(t = \ frac)⌘ begin t _ = \ frac = 367 \(c) = 6 \ text \ 7 \ \ text \ t _ = \ frac> = 2673 \(c) = 44) 44 мин 33 сек.








