Всегда проверяйте режим измерения перед подключением мультиметра к цепи и намеренно выбирайте диапазон измерительного прибора по измеряемому току. После первого измерения можно перейти в режим более низкого диапазона.
РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Цепи непрерывного тока имеют фиксированное напряжение, стабильный ток и только элементы плеча (резисторы).
Идеальный источник напряжения — это источник, в котором напряжение на зажимах, создаваемое внутренней мощностью (HED), не зависит от тока, создаваемого в нагрузке (рис. 6.1a). В этом случае выполняется равенство. Характерные напряжения идеального источника напряжения показаны на рис. 6.1 башня.
Идеальный источник тока — это источник, который обеспечивает электроэнергией нагрузку независимо от напряжения на клеммах источника. Рис. 6.2а. его характерное напряжение-вольт показано на рис. 6.2 круг.
В резисторах зависимость между напряжением и током определяется законом Ома вида
Пример схемы показан на рис. 6.3. ветвь, состоящая из многих последовательно соединенных элементов (источник E и резистор) или одного элемента (и) и узел и узел — это точки соединения трех или более ветвей, отмеченные сильной точкой. В приведенном примере есть ветвь и узел.

Кроме того, в цепи есть независимые замкнутые контуры, которые не содержат идеального источника тока. Их количество одинаково. В примере на рис. 6.3 эти числа, например, схемы с секторами пузырьков, и показаны на рисунке. 6.3Стрелка от эллипса показывает положительное направление цепи.
Связь между током и напряжением в цепи определяется законами Кирхгофа.
Первый закон Кирхгофа: алгебра токов, сходящихся в узле электрической цепи, равна нулю.
Токи, втекающие в узел, имеют знак плюс, а вытекающие — знак минус.
Второй закон Кирхгофа: алгебраическая сумма тенденций элементов замкнутой независимой цепи равна алгебраической сумме идеальных источников напряжения в этой цепи.
Тренд и ИМ получены при положительном сигнале. Если его положительное направление совпадает с адресом пересечения цикла, то синус использует отрицательное значение.
Для примера, показанного на рис. 6.3 Получение подсистем компонентных уравнений в соответствии с законом Ома
Согласно закону Кирхгофа, подсистема уравнения топологической цепи имеет вид
Расчет на основе закона Ома
Этот метод полезен для расчета относительно простых цепей источника e- включает в себя расчет сопротивления тех частей цепи, в которых
По цепи, где ток (или напряжение) известен, определяется неизвестное напряжение (или ток). Рассмотрим пример схемы, показанной на рис. 6.4, идеальный источник тока A и резистор Ом, Ом и Ом. Необходимо определить ток ветви и направление резистора.
(рис. 6.4, )
Напряжение на источнике тока (резисторе Ω) равно
Затем можно найти ток ветви и тренд
Используя первый закон Кирхгофа в форме, можно проверить полученные результаты. Подставляя вычисленные значения, мы получаем A, соответствующую источнику.
Зная поток ветви, нетрудно найти направление резистора (цена уже найдена).
По второму закону Кирхгофа. Обобщая полученные результаты, мы проверяем их выполнение.
Расчет цепи по уравнениям Кирхгофа
Рассчитайте ток и тренд фигурной цепи. 6.3 в и. цепь описывается системой уравнений (6.4) и (6.5), от которых идут ветви ветвей
из первого уравнения представляем и из третьего уравнения получаем.
Тогда из второго уравнения имеем
Из уравнения закона Ома следует, что
Легко видеть, что второй закон Кирхгофа выполняется.
Подставляя числовые значения
Только закон Ома дает тот же результат.
Может потребоваться знание токов в электрических цепях. Это можно определить как расчетным путем, так и путем прямого измерения. В последнем случае необходимую информацию можно получить из технических характеристик оборудования.
Расчёт электрических цепей с помощью законов Кирхгофа
Существует несколько методов расчета электрических цепей, которые различаются по определяемым параметрам и количеству необходимых вычислений.
Первый — это общий метод расчета схемы, но получаемые расчеты могут быть неоправданно большими. Этот метод расчета основан на законе Ома и Кирхгофа и используется для расчета небольших цепей с малым количеством контуров. Это система уравнений, состоящая из (q —1) уравнений узлов цепи и n уравнений независимых цепей. Независимые схемы характеризуются тем, что каждое новое уравнение схемы содержит по крайней мере одну новую ветвь, не включенную в предыдущую схему. Поэтому количество уравнений в системе уравнений при таком способе вычисления схем определяется следующим уравнением
В качестве примера рассчитаем цепь, показанную на схеме ниже
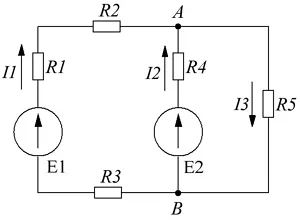
Пример электрической цепи, рассчитанной по закону Ома и Кирхгофа.
В качестве примера возьмем следующие параметры цепи: E1 = 50 В, E2 = 30 В, R1 = R3 = 10 Ом, R2 = R5 = 20 Ом, R4 = 25 Ом.
-
Составим уравнение по первому закону Кирхгофа. Так как узла у нас два, то выберем узел А и составим для него уравнение. Я выбрал условно, что токи I1 и I2 втекают в узел, а I3 – вытекает, тогда уравнение будет иметь вид

Таким образом, полученная система уравнений имеет вид
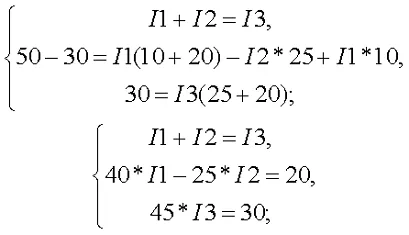
Решение этой системы дает следующие результаты: I1 ≈ 0,564 A, I2 ≈ 0,103 A, I2 ≈ 0,667 A.
Решив таким образом систему уравнений, можно доказать, что ток отрицательный. Это означает, что фактическое направление тока противоположно выбранному направлению.
Метод контурных токов
Приведенный выше метод расчета электрических цепей при анализе больших разветвленных цепей используется редко, так как приводит к неоправданно длительным вычислениям. Метод контурных токов является более распространенным и позволяет значительно сократить количество уравнений. В нем вместо токов в ветвях электрической цепи по второму закону Кирхгофа определяются так называемые контурные токи. Поэтому количество необходимых уравнений равно количеству независимых схем. В качестве примера рассчитаем цепь, показанную на схеме ниже
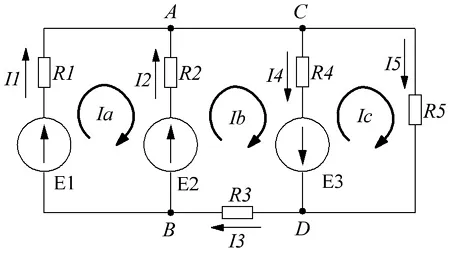
Расчет цепи по методу циркулирующего тока.
При расчете цепи по методу Ома и Кирхгофа необходимо решить систему из пяти уравнений. Метод контурных токов требует только трех уравнений.
В начале расчета определяются независимые цепи. В данном случае это E1R1R2E2, E2R2R4E3R3 и E3R4R5. Затем арбитражу присваивается произвольно направленный контурный ток с одинаковым направлением во всех частях выбранного контура. В этом случае для первого контура ток контура равен Ia, для второго Ib и для третьего Ic. Как показано на диаграмме, некоторые контурные токи соответствуют бифуркационным токам.
Другие токи можно найти как разность между двумя контурными токами
После выбора токов контура система уравнений может быть решена в соответствии со вторым законом Кирхгофа
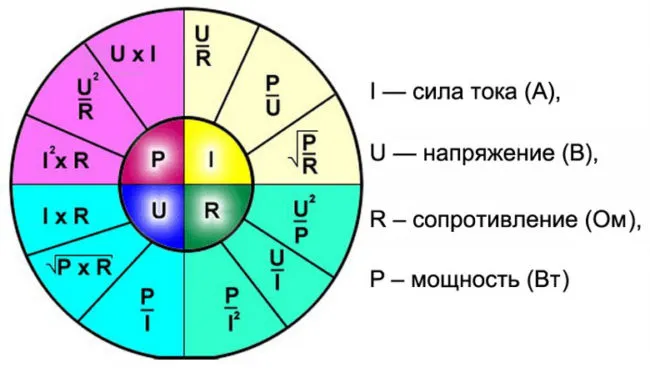
Рассчитайте цепь, показанную на схеме выше, используя следующие параметры: E1 = E3 = 100 В, E2 = 50 В, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишите систему уравнений.

В результате разрешения системы IA = I1 = 4,286 A, IB = I3 = 3,571 A, IC = I5 = -0,714 A, I2 = -0,715 A и I4 = 4,285 A. Негативно, фактическое направление противоположно предположению. Таким образом, токи i2 и i5 имеют направления, противоположные тем, что показаны на схеме.
Метод узловых напряжений
В дополнение к методу контуров применяется метод ключевых напряжений с еще меньшим числом уравнений, когда этот метод достигает своей цели, чтобы уменьшить сложность вычислений.
Где Q — количество узлов в электрической цепи.
Принцип расчета электрической цепи заключается в следующем: количество узлов в электрической цепи равно количеству узлов в цепи.
- Принимаем один из узлов цепи за базисный и присваиваем ему потенциал равный нулю;
- Для оставшихся узлов составляем уравнения по первому закону Кирхгофа, заменяя токи в ветвях по закону Ома через напряжение и сопротивление;
- После решения получившейся системы уравнений вычисляем токи в ветвях по обобщенному закону Ома.
Возьмем в качестве примера предыдущую схему и составим систему уравнений
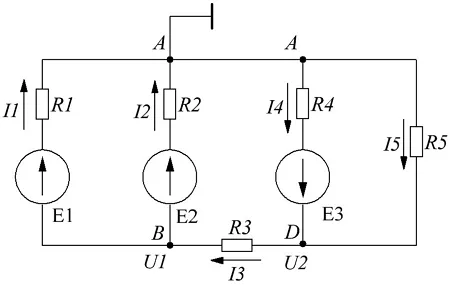
Схема решения уравнений методом динамических узлов.
Возьмите узел A в качестве базы и заземлите его. Для других узлов B и D составим уравнения в соответствии с первым законом Кирхгофа
Возьмем динамику b = u1 и d = u2. Токи в ветвях выражаются обобщенным законом Ома
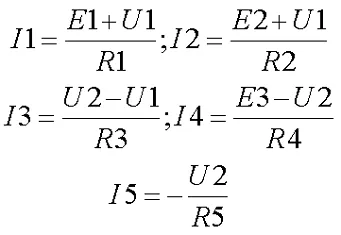
Полученная система имеет следующий вид
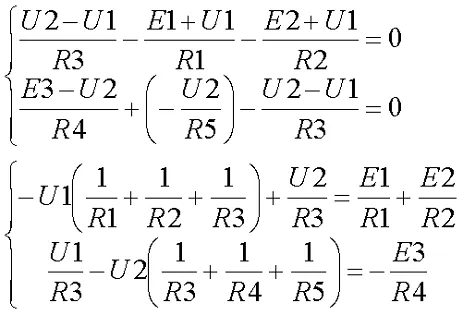
Рассчитайте цепь, показанную на схеме выше, используя следующие параметры: E1 = E3 = 100 В, E2 = 50 В, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишите систему уравнений.

В результате решения системы уравнений получите следующие результаты Мощность в узле B -U1 = -57,14 В и узле D -U2 = 14,29 В.
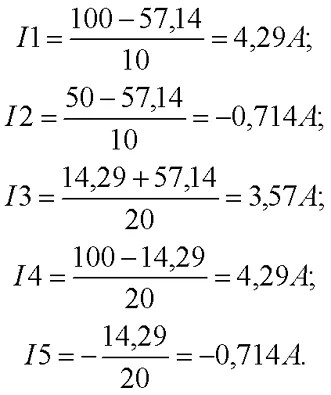
Результаты решения для токов i2 и i5 отрицательны, потому что фактическое направление токов противоположно направлению, показанному на графике. Эти результаты согласуются с результатами для той же цепи при использовании описанного метода тока.
Теория хороша, но нам нужно опробовать ее на практике.
Представьте себе, что есть трубка, в которую заталкивают камень. Вода, текущая по этой трубе, начинает замедляться, потому что она оказывает сопротивление. То же самое происходит и с электричеством.
Измерительными приборами
Если у вас есть измерительный прибор, то с его помощью очень легко найти источник питания. Все, что от вас требуется, — соблюдать правила измерения и знать правила безопасности.
Амперметром
При использовании измерителей силы тока помните, что они подключаются последовательно. Внутреннее сопротивление амперметра настолько мало, что его легко разрушить, если измерять сверх той цены, на которую он рассчитан.
Схема подключения амперметра показана на рисунке 3. Обратите внимание, что на измеряемом участке электрической цепи всегда должна быть нагрузка.
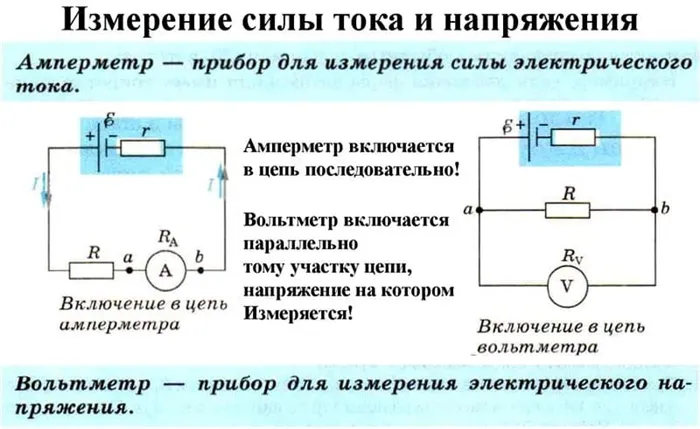
Рис. 3: Схема подключения амперметра
Большинство аналоговых схем амперметров, таких как на рисунке 4, подходят для измерения цепей непрерывного тока.
Рис. 4.Аналоговый амперометр
Наблюдайте за распределением на шкале амперометра. Первое значение разделения — 50 A, а в этих зонах все последующие — 10 A. В этом смысле гибкость амперметров ограничена.
При измерении постоянного тока при подключении амперметра необходимо соблюдать полярность детектора. Для подключения прибора необходимо отключить цепь. Это не всегда удобно. Иногда желательно рассчитывать ток по одному типу, особенно если измерения необходимо проводить в сложных электрических цепях.
Мультиметром
Преимущество мультиметров в том, что они многофункциональны. Современные мультиметры являются цифровыми. Они оснащены функциями измерения постоянного и переменного тока. В режиме измерения тока измеритель подключается к цепи так же, как и амперметр.
Всегда проверяйте режим измерения перед подключением мультиметра к цепи и намеренно выбирайте диапазон измерительного прибора по измеряемому току. После первого измерения можно перейти в режим более низкого диапазона.
Для переменного напряжения переключитесь в соответствующий режим. Когда цифры перестанут мигать, считайте значение с экрана.
Примеры
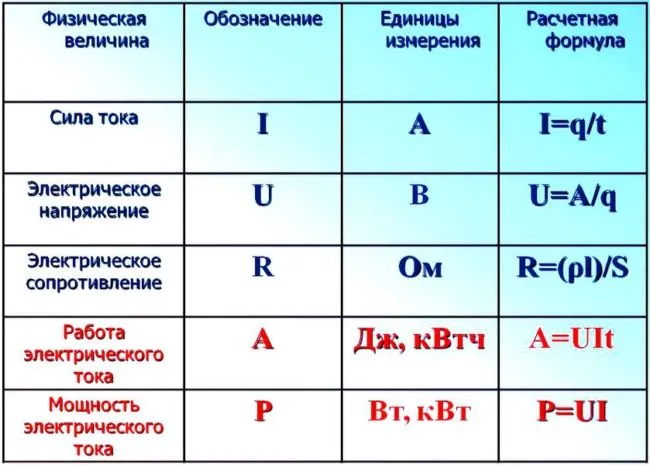
На простом примере покажите, как формула может быть использована для решения текущей вычислительной задачи.
Три резистора соединены параллельно в цепи (см. рисунок 5). Сопротивление резисторов равно: R1 =5 Омс-Р2 =25 Омс-Р3 = 50 Ом.Если поддерживается постоянное напряжение 100 В, необходимо рассчитать ток через каждый резистор и секцию.
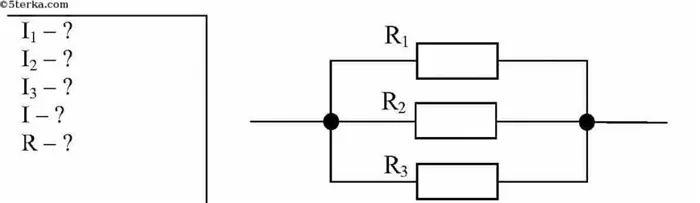
Рис. 5.Пример 1.
Решение: если элементы нагрузки соединены параллельно, то U = const, т.е. напряжение одинаково на всех резисторах и составляет 100 В. Тогда, согласно закону Ома, I = U / R
Для расчета параметров, необходимых для всей цепи, необходимо знать общее сопротивление цепи. Если элементы нагрузки в цепи соединены параллельно, то их общее сопротивление составляет
1 / R = 1/5 + 1/25 + 1/50 = 13 / 50- R = 50 /13 ≈ 3,85 (Ом)
Тогда: I = U / R = 100 В/3,85 Ом ≈ 26 А.
- Сила тока на сопротивлениях: I1 = 20 A- I2 = 4 A- I3 = 2 А.
- Сила тока, поступающего на рассматриваемый участок цепи равна 26 А.
Мощность чайника составляет 2 кВт. Чайник подключен к местной электросети 220 В, сколько электроэнергии потребляет этот прибор?
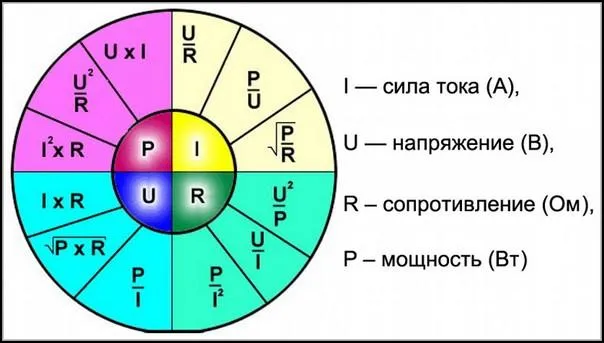
Используйте уравнение для нахождения напряжения и тока с учетом мощности: I =P/U.
- 2 кВт преобразим в ватты: 2 кВт = 2000 Вт.
- Подставляем данные: I = 2 000 Вт/ 220 В ≈ 9 А
- Ответ: Нагревательный элемент электрочайника рассчитан на 9 А.
Если известно, что сопротивление 5 Ом, АДР источника питания 6 В, а внутреннее сопротивление 1 Ом, рассчитайте ток в цепи.
Примените закон Ома к полной цепи и напишите: I =ε/(R + r’)
Ответ: Ток равен 1 A.
Если сопротивление нагревательного элемента составляет 40 Ω, сколько энергии будет потреблять электроплита за 2 часа работы?
В момент времени t электричество совершает работу A = U * I*t.
Напряжение в сети известно — оно составляет 220 В. Найдите силу тока по следующей формуле: I = U / R, тогда A = (U 2 / R)*t или
A = ((220 В) 2/40 Ом) * 2ч = 2420 Втч = 2,42 кВтч
ОТВЕТ: электрическая плита потребляет 2,42 кВт/ч электроэнергии за 2 часа работы.
Применяя формулу для расчета параметров электричества, вы можете использовать основные законы физики, чтобы найти неизвестные сведения о компонентах цепи или устройства и оценить их состояние. Во всех случаях необходимо определить известные параметры тока, которые могут быть использованы в последующих расчетах. Как правило, это напряжение, мощность или сопротивление нагрузки.
Если можно обойтись без измерений амперметром, лучше всего полагаться на расчеты, даже если требуется измерение напряжения. Такие измерения можно проводить без прерывания цепи, что невозможно при использовании амперметра.
Рассчитайте ток и тренд фигурной цепи. 6.3 в и. цепь описывается системой уравнений (6.4) и (6.5), от которых идут ветви ветвей
С помощью электродвижущей силы, внутреннего сопротивления и нагрузки
В некоторых учебниках для студентов есть так называемые конгрессные задачи. К ним относятся электродвигатели и значения внутреннего сопротивления.
Вспоминая закон Ома, электрическую интенсивность можно получить следующим образом: i= e/(r+r)
Это мощность, а R — внутреннее сопротивление. r представляет собой нагрузку.
С помощью закона Джоуля-Ленца
Некоторым людям трудно определить интенсивность потока, если таковой имеется.
Для решения задачи используйте закон Джоуля-Ленца: Q = I2RT
Исходя из этого типа, расчет должен быть следующим: i2 = qrt
Практические примеры
Чтобы правильно понять все вышеперечисленные типы, давайте рассмотрим некоторые примеры, которые можно найти в учебниках по физике.
Первый пример: вычислить ток от двух резисторов, используя последовательное и параллельное подключение к цели. Источник питания имеет напряжение 12 вольт.
Исходя из целевых условий, необходимо получить два значения: одно для последовательного соединения и одно для параллельного соединения.

Чтобы получить значения соединения последовательно, добавьте резистор и получите целое: R1+R2 = 1+2 = 3 Ом.
Кроме того, силу потока можно определить по закону Ома: i = u/r = 12/3 = 4 ампера
Для параллельных соединений расчет следующий: Ro = (r1*r2)/(r1+r2) = 1*2/3 = 2/3 = 0,67
Если применить закон Ома, то получится: i= 12*0,67 = 18a.
Второй пример: при соединении различных элементов цепи необходимо найти силу тока. На выходе 24 вольта, а резисторы с первого по третий — 1, 2 и 3 Ω соответственно.
В этом случае, используя формулу, определенную выше, получается следующий расчет: rrприв=(R2*R3)/(R2+R3) = (3*3)|(3+3) = 9/6 = 3/2 = 1,5 Ом.
Для этого типа схема выглядит следующим образом
Теперь определите силу тока: i = u/(r1+rprv) = 24/(1+1,5) = 24/2,5 = 9,6 ампера
Все это способы определения выносливости. Практикуя эти расчеты для типичных задач, вы сможете лучше понять, как рассчитать ток в электрической цепи!








