Интерференция света — Явление увеличения или уменьшения амплитуды результирующей световыx колебаний в разных точках пространства вследствие сложения двух когерентных световых волн.
Интерференция и дифракция
Интерференция — это изменение средней плотности потока энергии, вызванное суперпозицией волн.
Или немного по-другому: Интерполяция — это пространственное сложение волн, приводящее к временному постоянному распределению амплитуды суммарных колебаний.
Интерференцией волн света это комбинация волн, в которой существует временная постоянная картина усиления или ослабления суммарных колебаний света в различных пространственных точках. Термин интерференция в науку ввел Т. Юнг.
Условия возникновения интерференции
Для того чтобы суперпозиция волн имела постоянную интерференционДля получения стабильного изображения источники волн должны иметь одинаковую частоту и постоянную разность фаз. Такие источники называются когерентными. Когерентные волны — это волны, генерируемые когерентными источниками.
Поэтому только суперпозиция когерентных волн приводит к стабильному интерференционная картина.
В оптике для того, чтобы создать интерференционкогерентная схема, генерируются когерентные волны:
- делением амплитуды волны;
- делением фронта волны.
Условие минимумов интерференции
Амплитуда колебаний интерферирующих волн в рассматриваемой точке минимальна, если разность путей ( ) волн в этой точке содержит нечетное число полуволн ( ):
 Определение дифракции
Определение дифракции
Слово рефракция происходит от латинского и означает преломление.
Явление дифракции объясняется принципом Гюйгенса. Вторичные волны, испускаемые частями материи (среды), попадают за края препятствия на пути волны. Согласно теории Френеля, поверхность волны в любой момент времени является не только огибающей вторичных волн, но и результатом их интерференции.
Условия, при которых наблюдается дифракция
Дифракция особенно ярко выражена, когда размер препятствия меньше или сопоставим с длиной волны.
Волны любого типа могут быть как дифрагированными, так и возмущенными.
Условие минимумов интенсивности
При дифракции световоПри нормальных условиях падения для минимальной интенсивности в щели
 Условие главных максимумов интенсивности при дифракции на дифракционной решетке
Условие главных максимумов интенсивности при дифракции на дифракционной решетке
Условие максимума основной интенсивности дифракции света в дифракционной решетке при перпендикулярном падении лучей записывается так

Интерференция в тонких пленках. Альфа — угол падения, бета — угол отражения, желтый луч отделяется от оранжевого, они сводятся глазом в один и взаимодействуют.
Получить устойчивую интерференционную картину для света от двух пространственно отдельных и независимых источников света не так так же легко, как источники волн в воде. Атомы излучают свет за очень короткое время, и когерентность нарушается. Относительно простой такую шаблон получается следующим образом так, Рассеяние волн одного и того же цуга 1. Таким образом, интерференция получается при расщеплении исходного луча света на два луча при прохождении через тонкую пленку, напр.светлённых объективов. Луч света, проходя через плёнку толщиной » width=»» height=»» />где нм, толщина пленки 550:4=137,5 нм.
Лучи соседних частей спектра по обе стороны от
— минимальное требование,
где k=0,1,2. и — длины оптических путей первого и второго пучков, соответственно.
Явление интерференции наблюдается в тонком слое несмешивающихся жидкостей (парафин или масло на поверхности воды), в мыльных пузырях, бензине, крыльях бабочки, цвете беж и т.д.
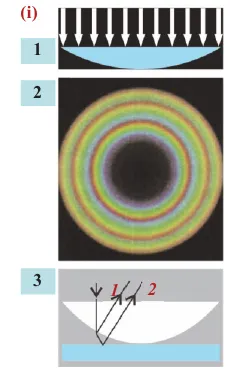
Кольца Ньютона
Другой метод получения стабильного интерференционной картины для света заключается в использовании слоя воздуха, основанного на одинаковой разнице путей двух частей волны, одна из которых отражается непосредственно от внутренней поверхности линзы, а другая прошла через слой воздуха внизу и затем отражается. Для этого выпуклую линзу помещают на стеклянную пластину, изогнутую вниз. Если линза освещается сверху монохроматическим светом светом у вас есть темное пятно в месте достаточного контакта линзы и пластины, окруженное чередующимися темными и концентрическими кольцами разных цветов. и светлыми концентрические кольца различной интенсивности. Более темные кольца соответствуют интерференционным минимумам, а светлые — темные кольца соответствуют самым большим, в то же время темные кольца соответствуют самым темным. и светлые кольца являются изоляторами с одинаковой толщиной воздушного зазора. Измерение радиуса светлогo или темное кольцо и определив его порядковый номер от центра, можно определить длину волны монохроматического света. Чем круче поверхность линзы, особенно вблизи краев, тем короче расстояние между соседними светлыми или темные кольца 2 .
Математическое описание
Интерференция двух плоских волн
Пусть имеются две плоские волны: _>\cdot \exp^
Согласно принципу суперпозиции, результирующее поле при пересечении этих волн определяется суммой:
_2″ width=»» height=»» />
Интенсивность определяется соотношением:
_1 <\mathbf E>^*_1+<\mathbf E>_1 <\mathbf E>^*_2+<\mathbf E>_2 <\mathbf E>^*_1 + <\mathbf E>_2 <\mathbf E>^*_2″ width=»» height=»» />
Откуда с учетом: , I_2=E^2_» width=»» height=»» /> :
><\mathbf E>_>\cdot \cos(<\mathbf k>_1<\mathbf r>_1-<\mathbf k>_2<\mathbf r>_2+_1 — _2)» width=»» height=»» />
Для простоты мы рассмотрим одномерный случай и выпрямление поляризованных волн, чтобы выражение для интенсивности можно было переписать в более простой форме:
E_>\cdot \cos(k_-k_)x+_1 — _2″ width=»» height=»» />
Интерференционная картина представляет собой чередование светлых и темных полос, шаг которых равен: -k_>» width=»» height=»» />
Примером такого случая является интерференционинтерференционная картина света, отраженного от поверхности плоскопараллельной пластины. свете.
Случай неравных частот
В некоторых учебниках и руководствах говорится, что что интерференция света возможно только для волн, генерируемых источником света с амплитудой или расстоянием между полями волновых фронтов. Это утверждение неверно. В смысле принципа суперпозиции. интерференция Она присутствует всегда, даже если волны от двух разных источников взаимодействуют. света. Правильнее было бы говорить о наблюдении или наблюдаемости. интерференционПоследнее не может быть постоянным. Последние не могут быть стабильными во времени, поэтому они размываются и исчезают. интерференционГраницы исчезнут. Рассмотрим две плоские волны с разными частотами:
_>\cdot \exp
Согласно принципу суперпозиции, результирующее поле при пересечении этих волн определяется суммой:
_2″ width=»» height=»» />
Устройство, имеющее определенное характерное время записи (время экспозиции), делает изображение интерференционизображение. В физической оптике интенсивность — это усредненный по времени поток световочерез единицу площади, перпендикулярной направлению распространения волны. Время вычисления среднего значения определяется временем интеграции фотодетектора, а для устройств, работающих в режиме накопления сигнала (камеры, фотопленка и т.д.), — временем экспозиции. Поэтому приемники оптического излучения реагируют на среднее значение тока энергии. То есть, сигнал фотодетектора пропорционален
>^2<>>_\tau» width=»» height=»» />
где <> означает среднее значение. Во многих научных и технических приложениях эта концепция обобщается на все волны, включая непланарные. Поскольку в большинстве случаев, например, в соединенных с интерференцией и дифракцией света, В задачах, где речь идет в основном о пространственном положении максимумов и минимумов и их относительной интенсивности, постоянными множителями, не зависящими от пространственных координат, часто пренебрегают. По этой причине его часто рассматривают:
1 \int_^ E^2 dt = I_1+I_2+2\frac<<\mathbf E>_><\mathbf E>_>> \int_^ \cos(\Delta\omega t+\Delta<\mathbf
>+\Delta\varphi) dt» width=»» height=»» />, где , I_2=E^2_» width=»» height=»» /> — Интенсивность волн
Зеркала Френеля.
На рисунке 2 показано схематическое изображение этого эксперимента. Два плоских зеркала и образуют почти перевернутый угол и дают два близко расположенных изображения и точечный источник. света. Вдали находится экран, который экранирует прямые лучи от источника. Только лучи, исходящие от источника, достигают экрана, таким На экран попадают только отражения от зеркал.
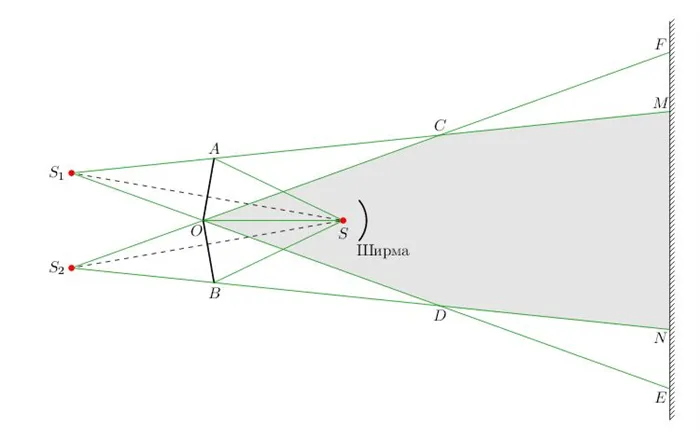 |
| Рис. 2: Интерференционный эксперимент с зеркалами Френеля. |
Как обычно, лучи света показаны зеленым цветом. Мы не указываем направления лучей, чтобы не перегружать картину. В конце концов, у вас за спиной геометрическая оптика, так можно легко понять путь лучей без указания их направления :-).
Лучи, отраженные от зеркала, образуют луч, который, как кажется, исходит из воображаемого изображения источника. Аналогично, лучи, отраженные от зеркала, образуют пучок света, как если бы они исходили от воображаемого изображения.
Эти лучи оказываются когерентными, поскольку мнимые источники и являются изображениями одного и того же источника, поэтому их частоты совпадают и сдвиг фаз между ними равен нулю. Поэтому в области, где лучи пересекаются, можно наблюдать постоянную интерференционмодель. Фактически, в любой точке этой области один и тот же луч пересекается в любой момент времени — с одним и тем же постоянным для этой точки фазовым сдвигом, вызванным разницей в путях от источников и .
Теперь мы видим, что эта ситуация вполне аналогична проблеме об интерференции волн от двух когерентных точечных источников, рассмотренных в конце предыдущей раздачи. В частности, амплитуда интерференционполос, наблюдаемых в эксперименте с зеркалом Френеля, составляет, где и — расстояние от прямой линии на экране. Значения и несложно найти геометрически.
Интерференция в тонких плёнках
Если вы смотрите на переливающийся разными цветами мыльный пузырь, на радужные отблески масляных или бензиновых пятен на поверхности воды, вы не воспринимаете ничего другого, как интерференцию света!
Давайте посмотрим на рис. 3 На поверхность тонкой прозрачной пленки падает световой луч .
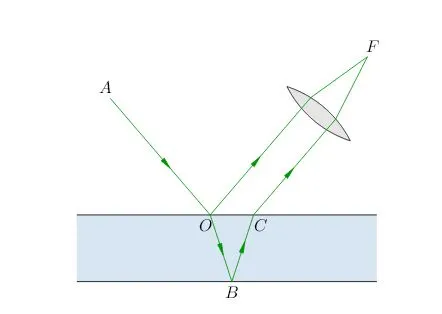 |
| Рис. 3. Интерференция на тонкой пленке |
Падающий луч разделяется на два луча: отраженный и преломленный. После вторичного отражения и преломления второй луч выходит из пленки параллельно отраженному лучу.
Оба луча фокусируются в точку с помощью фокусирующей линзы. Это, пожалуй, самая распространенная линза (при наблюдении интерференционПервый луч фокусируется оптической системой нормального глаза (при прямом наблюдении).
Две волны и, которые являются частью одной волны, являются когерентными. В действительности, две копии цуга сходятся в одной точке с постоянным сдвигом фаз между ними; этот сдвиг обеспечивается разницей в пути между волнами и. Поэтому волны взаимодействуют друг с другом и создают в окружающем пространстве изображение чередующихся максимумов и минимумов.
Предположим, что пленка освещается белым светом. светом. Как вы знаете, белые свет представляет собой смесь волн с различными частотами; эти частоты соответствуют цветам от красного до фиолетового. Например, предположим, что разница в длине волны между и равна интегральному числу длин волн красного цвета света. Тогда красная составляющая белого света будет усилен, и свет, отраженный от пленки свет будет казаться нам красным.
Небольшое изменение угла падения (или толщины пленки) также изменит разность путей. Таким образом, если поверхность пленки неровная (или если мы смотрим с немного другого направления), то новая разность путей может соответствовать целому ряду длин волн, например, зеленому цвету света. Теперь зеленый компонент белого цвета усиливается. света, и отражается от фильма. свет мы увидим зелёным.
Все это мы можем наблюдать, глядя на мыльный пузырь. Смещение поверхности приводит к постоянному изменению разности при определенном укорочении. Усиливается один цвет, затем другой, и в результате получается пузырь, который светится всеми цветами радуги.
Кольца Ньютона.
Возьмите плосковыпуклую линзу с достаточно большим радиусом сферической поверхности и поместите выпуклую линзу на стеклянную пластину. Если мы посмотрим сверху, то увидим через линзу концентрический интерференционконцентрические кольца (Рисунок 4).
 |
| рис. 4. ньютоновские кольца красного цвета свете |
Это кольца Ньютона; они были изучены Ньютоном, когда были освещены белым светом, так и монохроматическим светом. Происхождение колец Ньютона весьма схоже. интерференции в тонких слоях (рис. 5).
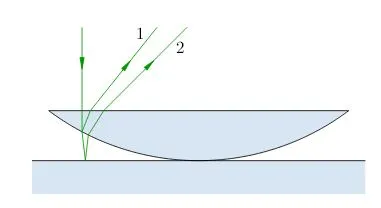 |
| Рисунок 5. Происхождение колец Ньютона |
Падающий луч разделяется на два луча 1 и 2, которые отражаются от сферической поверхности линзы и от пластины соответственно; получается и интерполируется разность путей между этими лучами. Три луча, показанные на рисунке, почти сливаются из-за небольшой кривизны поверхности линзы.
Вычислим радиусы светлых Кольца Ньютона. Предположим, что точка падения луча на сферическую поверхность находится на расстоянии y от пластины (рис. 6).
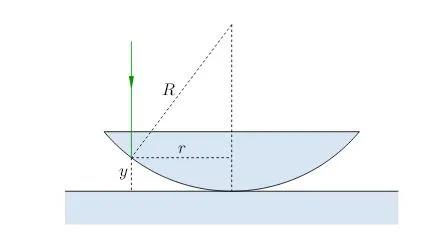 |
| Рисунок 6. Вычислить радиусы колец. |
Пусть — — радиус кривизны сферической поверхности линзы, — — расстояние точки падения от оси симметрии линзы. Теперь у нас есть это:
Поскольку воздушный слой очень тонкий ( ), этой величиной можно пренебречь по сравнению с :
Как и на рис. 5, путь второго луча примерно на 2y длиннее, чем путь первого луча. Однако разница в пути будет больше, чем 2y, потому что она вмешивается в важный эффект.
Отражение в левой части рис. 7 показывает отражение на границе раздела между воздухом и стеклом с левой стороны. Примечание: Фаза отраженной волны отличается от фазы падающей волны. Продемонстрирован общий факт: Отражение от оптически более плотной среды (т.е. среды с более высоким показателем преломления) изменяет фазу на, что соответствует сдвигу отраженной волны на половину длины волны по отношению к падающей волне.
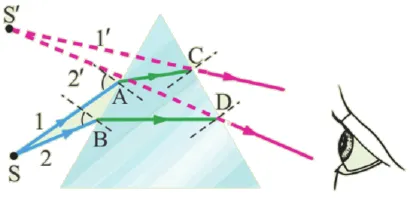 |
| Рис. 7. Отражение с полуволновым сдвигом и без него. |
В правой части рисунка 7 показано отражение на границе со стеклом. 7 показано отражение на границе раздела между стеклом и воздухом. Нет никакого сдвига фаз! В общем случае, при отражении от оптически менее плотной среды фазы отраженной и падающей волн совпадают.
Возвращаясь к рис. 5 и 6, мы видим, что луч 2 не только проходит дополнительный путь 2y, но и смещается на половину волны при отражении от границы раздела между воздухом и пластиной. На балку 1 не влияет смещение такого на границе раздела между воздухом и стеклом. Таким образом, разница в длине пути d между лучами 1 и 2 оказывается больше, чем 2y, на половину длины волны:
Короче говоря, схема формирования интерференционизображения следующим образом. Когда две волны одинаковой амплитуды встречаются, их сумма дает определенное значение амплитуды: от нуля до удвоенной амплитуды.
Интерференция света
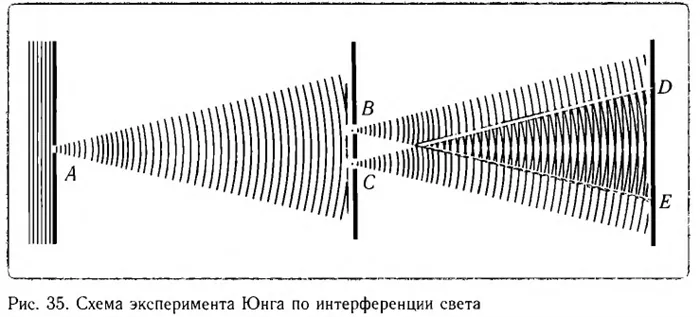
Для всех волн характерен эффект интерференции и дифракции. Если свет — волна, то также эти явления должны быть присущи ей. Такого мнения придерживались ученые, которые считали что свет имел волновой характер. Первое экспериментальное доказательство интерференции и дифракции света Томас Юнг в 1801 году.
Это интересно! Явление интерференции света был описан и объяснен в 1801 году, но сам термининтерференция света» был введен несколько позже, в 1803 году.
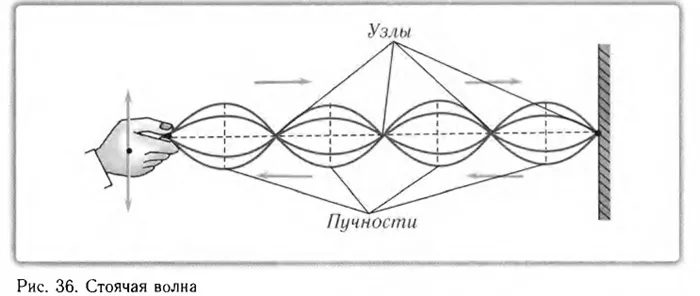
Интерференция механических волн
Для лучшего понимания этого явления интерференции, Давайте сначала объясним это на примере механических волн, которые легче наблюдать. Часто бывает так, что в среде одновременно распространяются несколько различных волн. Например, когда в помещении одновременно присутствуют несколько источников звука. Что же происходит, когда волны пересекают друг друга? Поясним это на примере волн, образующихся на поверхности воды.
Если бросить в воду два камешка, образуются две круговые волны. Если наблюдать за их распространением, то можно увидеть, что каждая волна проходит через другую. И она ведет себя так, как будто другой волны никогда не существовало. Именно так В воздухе может одновременно распространяться любое количество звуковых волн. И они не будут влиять друг на друга. Количество музыкальных инструментов в оркестре или голосов в хоре создает звуковые волны, которые мы воспринимаем одновременно. Звуки не превращаются в шум: Наши слуховые аппараты легко различают отдельные звуки.

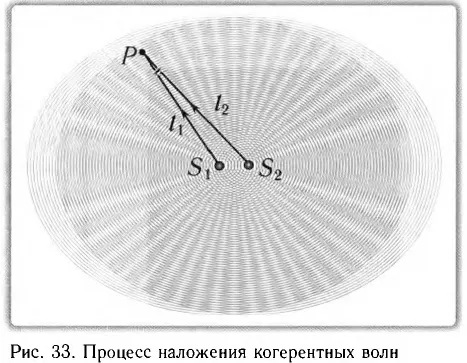
Теперь давайте более подробно рассмотрим процесс наложения волн. Для этого мы будем наблюдать за рябью на поверхности воды, исходящей от двух камней, брошенных в воду. Таким образом, мы увидим, что некоторые участки поверхности остаются ненарушенными, в то время как на других участках нарушенность увеличилась. Если два пика двух волн встречаются в одной точке, то возмущение поверхности воды в этой точке становится сильнее. Если гребень одной волны встречается со впадиной другой, поверхность воды в этой точке остается спокойной. Видно, что в любой точке среды колебания, вызванные двумя волнами, складываются. Результирующее смещение любой частицы в среде является алгебраической суммой смещений, которые произошли бы, если бы одна из волн распространялась в отсутствие другой.
Интерференция — это сумма волн в пространстве, которая производит постоянное во времени распределение амплитуд результирующих колебаний частиц в среде.
Чтобы определить условия, при которых человек наблюдает интерференция Возбудим две круговые волны в ванне с помощью двух сфер, прикрепленных к стержням и вибрирующих по гармоническому закону.

Теперь давайте воспроизведем это явление интерференции схематично. В любой точке M на поверхности воды колебания вызываются двумя волнами от источников O1 и О2 (Амплитуды колебаний, создаваемых двумя волнами в любой точке M, различны, если волны движутся по разным путям d1 и г2. Однако, если расстояние l между источниками намного меньше этих путей, можно считать, что две амплитуды приблизительно равны.
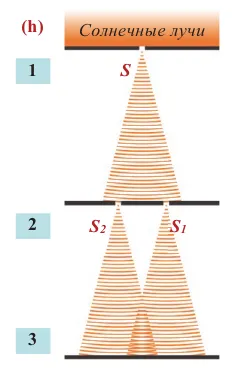
Результат сложения волн, приходящих в точку М, зависит от разности фаз между ними. Проходя различные расстояния d1 и г2 волны имеют разность путей, определяемую формулой:
Если разность путей равна длине волны λ, то вторая волна отстает от первой на один период. Поскольку волна проходит расстояние, равное ее длине волны, за один период, их фазы совпадают в точке, где две волны встречаются. Если в этой точке волны имеют пики, то пики совпадают; если впадины, то впадины совпадают.
Интерференция света
Ели свет — Если фаза волны — это поток волн, то следует рассмотреть явление интерференции. Однако получить интерференционЕсли два независимых источника (например, две лампы) попеременно создают минимум и максимум, мы должны быть в состоянии нарисовать картину волн, когда они поднимаются и опускаются. света (например, две лампы) невозможно. Включение второй лампы только увеличивает яркость поверхности, но не создает картину минимальных и максимальных значений. Это происходит потому, что волны не координируются. Для достижения постоянного интерференционстабильная картина требует согласованной, т.е. когерентной световые волны. Они должны иметь равные длины волн и постоянную разность фаз во времени в каждой точке пространства.
Однако наблюдать интерференцию света Это все еще возможно. Вы замечали это, когда пускали мыльные пузыри или рассматривали масляную пленку на поверхности воды.

Томас Юнг был первым ученым, который дал объяснение изменению цвета тонких пленок путем добавления волн. Он предположил, что одна волна отражается от внешней поверхности пленки, а другая — от внутренней. Это приводит к явлению, называемому интерференцией световых волн .
Усиление света когда дифрагированная волна задерживается относительно отраженной волны на целое число длин волн. Здесь применимо понятие максимума, упомянутое выше:
Если вторая волна задержана по отношению к первой волне на половину длины волны или на нечетное число полуволн, то затухание составляет света. Здесь действует условие минимумов, из которых мы также уже говорили:
D d = ( 2 k + 1 ) λ 2 .
Четкая интерференционТакое изображение создается благодаря тому, что волны, отраженные от внутренней и внешней оболочек тонкой пленки, когерентны. Когерентность этих волн объясняется тем, что они являются частью одного и того же же светового луча.
Юнг пришел к выводу, что разнообразие цветов в мыльной пленке обусловлено различными длинами волн. Если при освещении белым светом пленка имеет неравномерную толщину. светом и вы получите разные цвета.
Простую интерференционную картину также получают, помещая на поверхность стекла плосковыпуклую линзу, сферическая поверхность которой имеет большой радиус кривизны. Полученная интерференционная картина таким называется кольцами Ньютона.
Исаак Ньютон исследовал интерференционрисунок, полученный в тонком слое воздуха между стеклом и линзой, не только белого цвета, но и с свете, но и когда линза освещалась монохроматическим светом. Поэтому он обнаружил, что радиусы колец с одинаковым атомным номером увеличиваются по мере продвижения от фиолетового конца спектра к красному. Поэтому красные кольца имеют максимальный радиус. Расстояние между соседними кольцами уменьшается по мере увеличения радиуса.
Ньютон мог получать кольца, но не мог объяснить их появление. Но Юнг сделал это. Его эксперимент показал, что волна определенной длины падает почти вертикально на плоскую изгибающуюся линзу. Волна 1 обусловлена отражением от изогнутой поверхности линзы на границе раздела воздух-стекло, а волна 2 — отражением от пластины на границе раздела воздух-стекло.
Как и на рис. 5, путь второго луча примерно на 2y длиннее, чем путь первого луча. Однако разница в пути будет больше, чем 2y, потому что она вмешивается в важный эффект.
Интерференция света
В этом видеоуроке мы вместе с детьми вспоминаем, что называется интерференцией волны и при каких условиях происходит это явление. Мы выясним, в чем суть этого явления. интерференции света. Мы ознакомимся с первыми попытками наблюдения за интерференцией света. А также Помните об условиях образования интерференционВспомним условия образования максимумов и минимумов.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим обучающим видео в комплекте, вам необходимо добавить его в свой личный кабинет, купив его в каталоге.
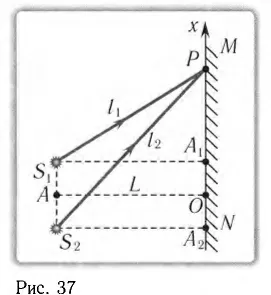

Когда разница в пути волн равна нечетному числу полуволн, волны приходят в точку P в противофазном состоянии и ослабляют друг друга. Это соответствует выполнению минимального условия:
Интерференция волн
В ходе исследования вы наблюдали эффект сложения когерентных волн, генерируемых на поверхности воды гармоническими колебаниями сфер-осцилляторов с одинаковой частотой.
Когерентные волны — это волны, порожденные различными источниками колебаний, которые имеют одинаковую частоту колебаний и постоянную разность фаз, не зависящую от времени.
Колебания, возникающие в результате суммы когерентных волн, либо усиливаются, либо ослабляются в зависимости от разницы между расстояниями между источником колебаний и точкой их встречи — это происходит интерференция волн.
Интерференция волн — это усиление или ослабление амплитуды колебаний результирующей волны в результате сложения когерентных волн (лат. «inter» — взаимный, «ferio» — встречаться).
Усиление или ослабление амплитуды результирующей волны определяется условиями максимальной и минимальной амплитуды. интерференции.
Условие максимума интерференции
Максимум интерференции Он наблюдается в точках пространства (поверхности), где максимумы кумулятивных волн перекрываются. Она зависит от разницы в путях, пройденных волнами от источника колебаний до этой точки.
Интерференционный максимум результирующей волны образуется в точках, где разность путей сложенных волн равна нулю или четному числу полуволн (разность фаз равна нулю или четному числу) (d):
Здесь k — порядок максимума и целое число: k= 0,1, 2. такая связь:
При использовании выражения (1) в формуле (2) для максимальной разности фаз получаются следующие результаты интерференции получим:
Поскольку ширины сложенных волн равны, амплитуда результирующего колебания в этом случае равна сумме ширин исходных волн (e) :
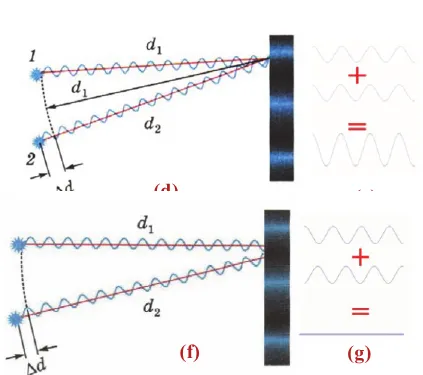
Условие минимума интерференции
Минимумы интерференции наблюдаются в тех точках пространства, где волны достигают противофазного состояния. Максимум одной волны совпадает с минимумом другой. В результате волны ослабляют друг друга.
Минимум интерференции происходит в точках, где разность путей суммарных волн равна нечетному числу полупериодов полуволн (разность фаз равна нечетному числу (f) :

Если в этом случае амплитуды добавочных волн равны, то в точке минимума интерференции амплитуда результирующей волны уменьшается до нуля (g) :
Интерференция света
Интерполяция является характерным свойством всех типов волн, таких как. и световых. Так, две световыКогда волны складываются в пространстве, они могут усиливать или ослаблять друг друга, и даже могут быть и такой вариант: свет + свет = темнота.
Интерференция света — Явление увеличения или уменьшения амплитуды результирующей световыx колебаний в разных точках пространства вследствие сложения двух когерентных световых волн.
В течение многих лет было невозможно найти способ создания когерентных икс-волн световых-волны, поэтому было невозможно световыневозможно было продемонстрировать способность Х-волн к интерференции.
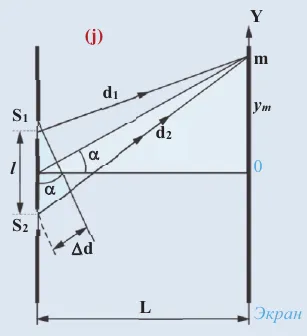
Только в начале XIX века Томас Юнг, используя простой прибор, смог наблюдать интерференцию света (h) .








