Идеальный одноатомный газ. Как изменяется внутренняя энергия одноатомного идеального газа

Содержание

1. кинетическая энергия непрерывного хаотического движения частиц тела. 2. потенциальная энергия молекул (индивидов), обусловленная силами взаимодействия алмазов. 3. индивидуальная электронная энергия. 4. эндогенная ядерная энергия.

Идеальный одноатомный газ. Формула внутренней энергии. Решение задач

Изучение свойств и поведения идеальных газов является ключом к пониманию физики в целом. В этой статье мы рассмотрим, что входит в понятие идеального газа человека, его положение и уравнения, описывающие его внутреннюю энергию. Студенты также решат некоторые проблемы, связанные с этим вопросом.

Каждый ученик знает, что газ — это одно из трех совокупных состояний вещества. Он отличается от твердых тел и жидкостей тем, что не сохраняет свой объем. Он также не сохраняет свою форму и всегда заполняет все объемы. Действительно, последнее свойство применимо к ТАК НАЗЫВАЕМОМУ идеальному газу.

Концепция идеального газа тесно связана с теорией молекулярных скоростей (MKS). Согласно ей, частицы в газовой системе хаотично движутся во всех направлениях. Их скорость соответствует максвелловскому распределению. Частицы не взаимодействуют друг с другом, и расстояние между ними намного больше их размера. Если все эти условия выполняются с определенной степенью точности, газ можно считать идеальным.

Все реальные среды практически идеальны, когда плотность мала, а абсолютная температура высока. Кроме того, они должны состоять из химически инертных молекул или индивидуумов. Так, водяной пар не считается идеальным газом из-за наличия сильных водородных взаимодействий между молекулами H2O, тогда как воздух, состоящий из неполярных молекул, является таковым.

Закон Клапейрона-Менделеева

При анализе, в терминах MCT, поведение газового баланса может привести к следующим уравнениям, которые связывают основные термодинамические параметры системы.

Здесь давление, объем и температура обозначаются латинскими буквами P, V и T соответственно. Цена n — это количество вещества, позволяющее определить число частиц в системе; R — постоянная газа, которая не зависит от химических свойств газа. Другими словами, каждый идеальный газ объемом 1 моль будет расширяться при нагревании на 1 К и совершать работу, равную 8,314 дж/(к*моль).

Записанное уравнение называется универсальным законом Клапейрона-Менделеева. Почему; назван в честь французского естествоиспытателя Эмиля Клапейрона в 30-х годах XIX века, который изучал ранее установленный экспериментально газовый закон. Позже Дмитрий Менделеев привел его к современной форме, введя константу R

Внутренняя энергия одноатомной среды

Идеальный газ человека отличается от многоатомного тем, что частица имеет только три степени свободы (специфическое фороподобное движение вдоль трех пространственных осей). Это приводит к следующему виду средней кинетической энергии человека.

Скорость V называется среднеквадратичной скоростью. Масса и постоянная Больцмана человека обозначаются как M и KB соответственно.

Согласно определению внутренней энергии, она представляет собой сумму кинетической и динамической составляющих. Давайте рассмотрим подробнее. Поскольку идеальный газ не имеет потенциальной энергии, его внутренняя энергия является кинетической энергией. Каков его тип? Вычислив энергию всех частиц n в системе, мы получаем следующее уравнение для внутренней энергии u человека.

Согласно Федеральному закону N273-ФЗ «Об образовании в Российской Федерации» в организации обеспечения образовательной деятельности следует отметить, что обучение и воспитание обучающихся с ограниченными возможностями здоровья организуется совместно с другими обучающимися либо в отдельных классах или группах.

Внутренняя энергия одноатомного идеального газа

Обратите внимание, что молекулы идеального газа представлены в виде материальных точек, которые не взаимодействуют друг с другом на расстоянии. Отсутствие сил взаимодействия между молекулами означает, что потенциальная энергия взаимодействия молекул постоянна. Поскольку молекулы не изменяются во время теплового процесса, полная энергия покоя самих молекул также постоянна. Поэтому внутренняя энергия идеального одноатомного газа равна сумме кинетической энергии метафорического движения молекул и константы.

Внутренняя энергия газа обозначается U и описана выше.

$\U=E_<k1>+E_<k2>+\dots +E_<kN>+const \qquad (1)\» width=»352″ height=»18″ />где — полная кинетическая энергия образного движения молекул; N — число молекул в газе. Предположим, что средняя кинетическая энергия () молекул равна<img decoding=$ _k\right\rangle =\frac+E_+\dots +E_> \qquad (2)\» width=»305″ height=»38″ />

В соответствии с законом равномерного распределения энергии по степеням свободы.

-постоянная Больцмана-Т — температура Кельвина.

Внутренняя энергия идеального газа из атомов может быть записана как

$\U=N\left\langle <\varepsilon>_k\right\rangle +const=N\frac<3><2>kT+const \qquad (5)\» width=»364″ height=»38″ />Константу в уравнении (5) обычно опускают, так как она не участвует в расчете.Уравнение (5) показывает, что внутренняя энергия идеального газа определяется его температурой. Она является функцией состояния и не зависит от процессов, которые происходили до достижения газом этой температуры. Изменение внутренней энергии идеального газа определяется только его начальным и конечным состояниями и не зависит от характера процесса.Уравнение (5) часто используется в следующей форме<img decoding=$ <2>\frac<\mu>RT=\frac<3><2>\nu RT \qquad (6)\» width=»238″ height=»42″ />

где m — масса газа — молекулярная масса газа — универсальная постоянная газа — количество вещества.

Теплоемкость одноатомного идеального газа

Для равностороннего треугольного процесса, происходящего в идеальном газе, работа равна нулю (A), поэтому первый закон термодинамики гласит

где — теплоемкость постоянного объема газа. Используя уравнения (8) и (6), имеем

$\C_V\Delta T=\frac<3><2>\nu R\Delta T\to \ C_V=\frac<3><2>\nu R \qquad (9)\» width=»333″ height=»38″ />Уравнение (10) может быть использовано для расчета молекулярной теплоемкости любого газа атомов в постоянном объеме.Молекулярная теплоемкость ( ) отдельного атомарного газа в равновесном процессе связана с уравнением связи Мейера<img decoding=$ =c_<\mu V>+R=\frac<5><2>R \qquad(11)\» width=»239″ height=»39″ />

Примеры решения задач

Задание	Получите формулу для вычисления молярной теплоемкости ( ) одноатомного идеального газа ( ) для процесса, в котором масса газа остается постоянной, закон изменения процесса задан выражением: .
Решение	Первое начало термодинамики запишем в дифференциальной форме:

$\\delta Q=\frac<3><2>\nu RdT+pdV \qquad (1.1)\» width=»242″ height=»38″ />Где<img decoding=$ dT=\frac<3><2>\nu RdT+pdV\to \ c_<\mu>=\frac<3r><2>+\frac<\nu dT> \qquad (1.2)\» width=»437″ height=»39″ />

Из уравнений процесса: мы знаем, что

$\\frac<dV><dT>=-\frac<2\cdot const><T^3> \qquad (1.3)\» width=»211″ height=»39″ />Из уравнения закона для идеального газа мы имеем<img decoding=$ \qquad (1.4)\» width=»270″ height=»38″ />

Используя уравнения (1.3) и (1.4) и уравнение процедуры, уравнение (1.2) преобразуется следующим образом

$\c_<\mu>=\frac<3R><2>-\frac<\nu RT\cdot 2\cdot const><\nu T^3V>=\frac<3R><2>-\frac<R\cdot 2\cdot const><T^2V>=\frac<3R><2>-\frac<R\cdot 2\cdot const><const>=-0,5R\» width=»623″ height=»37″ /><img decoding=$

$\\Delta U=U_2-U_1=\frac<3\nu R><2>\left(T_2-T_1\right) \qquad (2.1)\» width=»340″ height=»38″ />Процесс МА условно является изотермическим, так как в изотермических процессах температура не изменяется.На рисунке 1 показано, что оба процесса начинаются из одной и той же точки. Поэтому эти процессы имеют одинаковые параметры. Это означает, что начальные температуры процессов MA и MV одинаковы. Давайте посмотрим, что происходит с температурой во время процесса MA.Температуры в точках M и A равны в соответствии с процедурой (). Сравнивая температуры, можно определить, повышается ли температура в процессе MB. Для этого рассмотрите варианты внутри страны. Равнопространственные процессы следуют закону Шарля.Из рисунка 1 видно, что температура процесса MB снижается. Поэтому в процессе MB внутренняя энергия идеального газа уменьшается.<blockquote>Решение проблем — это занятие, которое нравится не всем. Здесь мы стараемся потратить как можно больше времени без ущерба для качества решения. Предметом данной статьи является вопрос внутренней энергии.</blockquote><h2>Функция состояния</h2>Наиболее важным свойством внутренней энергии является то, что она является функцией состояния термодинамической системы. То есть, внутренняя энергия однозначно определяется набором макроскопических параметров, характеризующих систему, «предысторией» системы, то есть предыдущим состоянием системы, и не зависит от того, как именно это состояние было достигнуто.Таким образом, когда система переходит из одного состояния в другое, изменение ее внутренней энергии определяется исключительно исходным конечным состоянием системы и не зависит от пути перехода из исходного состояния в конечное. Если система возвращается в исходное состояние, то изменение ее внутренней энергии равно нулю.Опыт показывает, что существует только два способа, с помощью которых тело может изменить свою внутреннюю энергию.— Механические проекты — теплопередача.Проще говоря, существует только два основных способа нагрева чайника. Натрите его чем-нибудь и подожгите :-). Давайте рассмотрим эти методы подробнее.<h2>Изменение внутренней энергии: совершение работы</h2>По мере того, как организм выполняет свою работу, внутренняя энергия организма увеличивается.Например, ноготь после удара молотком нагревается и слегка деформируется. Однако температура — это мера средней кинетической энергии частиц в теле. Нагревание гвоздя указывает на увеличение кинетической энергии его частиц. Частицы ускоряются под действием удара молотка и трения гвоздя.Деформация есть не что иное, как смещение частиц между собой — после удара гвоздь испытывает сжимающую деформацию, его частицы перемещаются ближе друг к другу и силы отталкивания друг с другом увеличиваются, что приводит к увеличению динамической энергии частиц гвоздя.Таким образом, внутренняя энергия гвоздя увеличилась. Это был результат проделанной над ним работы — работа была совершена молотком и силами трения о доску.Когда работа выполняется самим телом, внутренняя энергия тела уменьшается.Предположим, например, что сжатый воздух в изоляционном контейнере под поршнем расширяется и поднимает некоторый вес (процесс в изоляционном контейнере называется изоляцией — см. ниже). (Процессы изоляции изучаются во время первой проверки закона). В таком процессе воздух охлаждается — его молекулы сталкиваются с движущимся поршнем, отдавая ему часть своей кинетической энергии. (Аналогично футболист останавливает быстро летящий мяч ногами и снижает его скорость, убегая от него). Таким образом, внутренняя энергия воздуха уменьшается.Таким образом, воздух выполняет свою задачу за счет своей внутренней энергии. Поскольку контейнер изолирован, в воздух не поступает энергия из внешних источников, и воздух может черпать энергию для выполнения задач только из собственных запасов.<h2>Изменение внутренней энергии: теплопередача</h2>Теплопередача — это процесс передачи внутренней энергии от теплого тела к холодному, механическая задача. Тепло может передаваться через прямой контакт или через промежуточную среду (вакуум). Теплопередачу также называют теплообменом.Существует три вида теплопередачи: обработка, синагога и излучение.Сейчас мы рассмотрим их более подробно.<blockquote>Сравните внутреннюю энергию газа, оставшегося в бутылке после равновесного нагревания, с внутренней энергией газа в открытой бутылке до нагревания</blockquote><h2>Как изменяется внутренняя энергия идеального газа человека при увеличении давления в три раза и уменьшении объема в два раза?</h2>Как изменяется внутренняя энергия идеального газа человека при увеличении давления в три раза и уменьшении объема в два раза?<img decoding=$

Таким образом, U = 3/2 * 3P * V / 2 = 6PV / 4 = 1, 5PV

Ответ: U увеличивается в 1,5 раза.

Во сколько раз изменится давление индивидуального идеального газа, если средняя кинетическая энергия теплового движения его атомов увеличится в 3 раза, а объем газа уменьшится в 2 раза?

Во сколько раз изменится давление индивидуального идеального газа, если средняя кинетическая энергия теплового движения его атомов увеличится в 3 раза, а объем газа уменьшится в 2 раза?

Как изменяется внутренняя энергия постоянного объема индивидуального идеального газа при уменьшении изопространственного давления?

1) обратно пропорционально увеличению давления 2) увеличивается или уменьшается при изменении объема 3) уменьшается прямо пропорционально давлению 4) увеличивается или уменьшается при изменении молекулярной массы газа.

На этой странице вы найдете ответ на вопрос Как изменяется внутренняя энергия идеального одноатомного газа при увеличении давления в три раза и уменьшении объема в два раза, который относится к категории Физика. Уровень сложности вопросов соответствует базовым знаниям учащихся 10-11 классов. Для получения дополнительной информации воспользуйтесь поисковой системой, чтобы найти другие соответствующие вопросы. Кроме того, нажмите на кнопку в верхней части страницы и создайте новый вопрос, используя ключевые слова, соответствующие вашим критериям. Обсудите эту тему с посетителями вашей страницы. Возможно, их ответы помогут вам найти информацию, которую вы ищете.

При анализе, в терминах MCT, поведение газового баланса может привести к следующим уравнениям, которые связывают основные термодинамические параметры системы.

Презентация к уроку по физике «Внутренняя энергия идеального одноатомного газа» 10 класс

Согласно Федеральному закону N273-ФЗ «Об образовании в Российской Федерации» в организации обеспечения образовательной деятельности следует отметить, что обучение и воспитание обучающихся с ограниченными возможностями здоровья организуется совместно с другими обучающимися либо в отдельных классах или группах.

Курсы повышения квалификации

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 учебных материалов для школьного и домашнего обучения

Внутренняя энергия идеальных газов

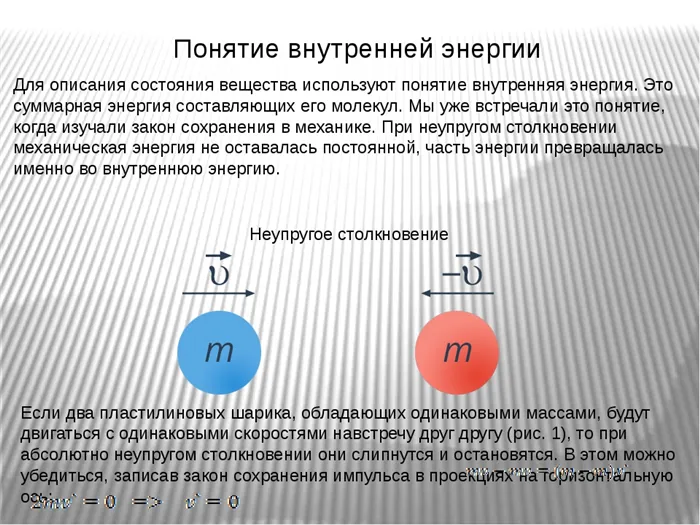
Термин «внутренняя энергия» используется для описания состояния материи. Это общая энергия составляющих его молекул. Мы уже сталкивались с этой концепцией при изучении законов сохранения в технике. При неупругих столкновениях механическая энергия не сохраняется постоянной, но часть энергии преобразуется во внутреннюю энергию. Если два глиняных шарика одинаковой массы движутся с одинаковой скоростью друг к другу (рис. 1), то при абсолютно неупругом столкновении они прилипнут друг к другу и остановятся. Это можно понять, записав закон сохранения импульса в поперечной проекции.

До столкновения полная кинетическая энергия системы была следующей После столкновения и остановки шарика кинетическая энергия системы составила Таким образом, потерянная системой энергия (в данном случае вся кинетическая энергия) перешла во внутреннюю энергию шара. Другими словами, молекулы или атомы, составляющие вещество, приобрели дополнительную кинетическую энергию и движутся быстрее. Кроме того, при введении одного из макропараметров — температуры — пришлось столкнуться с понятием внутренней энергии в молекулярно-кинетической теории. Температура — это мера внутренней энергии материи. Если речь идет об идеальном или разреженном реальном газе, то потенциальной энергией взаимодействия его частиц можно пренебречь. В этом случае температура пропорциональна средней кинетической энергии молекул. Почему в среднем? Потому что число молекул в этом количестве вещества обычно огромно. Поскольку энергия отдельных молекул не представляет интереса, происходит статистический процесс и используется средняя энергия. Для газов, жидкостей и твердых тел высокой плотности гораздо сложнее выразить внутреннюю энергию в терминах макроскопических параметров. Внутренняя энергия очень плотных газов также может зависеть от объема, особенно если расстояния между молекулами малы, так как потенциальная энергия взаимодействия между частицами вносит значительный вклад во внутреннюю энергию. Таким образом, зависимость между температурой и средней кинетической энергией для идеальных, разреженных реальных газов выглядит следующим образом

Тогда внутренняя энергия этих газов равна общей кинетической энергии всех молекул. Другими словами, это произведение средней кинетической энергии молекул и их количества. Внутренняя энергия обычно выражается в виде большой буквы U и измеряется в джоулях.