В замкнутой системе векторная сумма импульсов всех тел системы остается постоянной по отношению к взаимодействиям тел этой системы между собой.
Импульс
USHD Codemeter Темы: толчок тела, импульс системы тела, как поддерживается импульс.
Толчок тела — это векторная величина, равная произведению веса тела на его скорость.
Специального блока импульсов не существует. Размерность толчка — это просто произведение размерности массы на размерность скорости.
Почему концепция импульса интересна? Оказывается, его можно использовать для придания несколько иной и очень полезной формы второму закону Ньютона.
Второй закон Ньютона в импульсной форме
Не в последнюю очередь — чистое воздействие силы на тело массы. Начнем с обычной символики второго закона Ньютона.
Поскольку ускорение тела равно производной от вектора его скорости, второй закон Ньютона переформулируется следующим образом
Поместите твердое место под производным знаком:.
Как вы видите, левая часть содержит производную от импульса.
Соотношение (1) — это новая письменная форма второго закона Ньютона.
Второй закон Ньютона в форме импульса. Производная импульса тела — это чистый эффект силы, приложенной к телу.
Также можно сказать, что Составляющая силы, действующей на тело, равна скорости изменения импульса тела.
Производная типа (1) может быть заменена основанием для конечной дополнительной платы.
В этом случае на тело действует средняя сила в течение определенного периода времени. Чем ниже цена, тем ближе причина к производной, и тем ближе средняя сила приближается к своему мгновенному значению в конкретный момент времени.
В принципе, времени очень мало. Например, это время столкновения мяча со стеной и средняя сила, действующая на мяч со стороны стены во время удара.
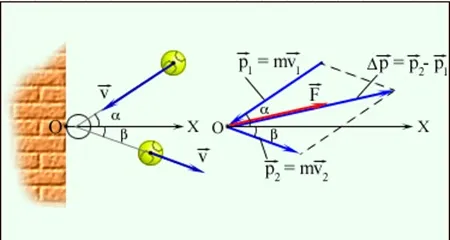
Вектор в левой части уравнения (2) называется изменением импульса во времени. Изменение импульса — это разница между концом края и исходным вектором. Другими словами, импульс тела в определенный начальный момент времени, импульс тела через некоторое время, изменение импульса — это разница.
Еще раз подчеркнем, что изменение импульса — это разность векторов (рис. 1).
 |
| Рис. 1. Изменение импульса |
Например, мяч летит перпендикулярно стене (импульс до равного удара) и отскакивает назад, не теряя скорости (импульс после удара). В modulo () импульс не изменился, но есть изменение импульса.
Геометрически эта ситуация показана на рисунке 2.
 |
| Рис. 2. Изменение импульса при отскоке назад |
Как мы видим, мера импульса равна удвоенному первоначальному импульсу мяча.
Перепишите тип (2) следующим образом.
Или запишите изменение импульса, как указано выше:.
Эта величина называется импульсом импульса. Для импульса силы не существует конкретной единицы измерения — стимул импульса силы является просто произведением размеров силы и времени.
(Обратите внимание на то, что оказалось еще одной возможной единицей измерения импульса тела).
Словесная формулировка равенства (3) выглядит следующим образом. Изменение импульса тела равно импульсу силы, действующей на тело за определенный промежуток времени. Конечно, он снова является вторым законом Ньютона в форме толчка.
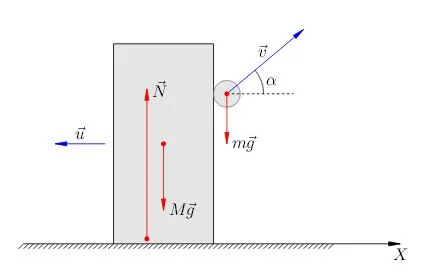
Пример вычисления силы
В качестве примера реализации второго закона Ньютона в форме толчка рассмотрим следующую задачу
Проблема. Шар массой G, летящий горизонтально со скоростью м/с, врезается в гладкую вертикальную стену и отскакивает назад, не теряя скорости. Угол падения шарика (т.е. угол между направлением его движения и углом, перпендикулярным стене) равен. За ударом следует с. Найдите среднюю силу, приложенную к мячу во время удара.
Решение. Сначала покажите, что угол отражения равен углу падения. Это означает, что мяч отскочит от стены под тем же углом (рис. 3).
 |
| Рис. 3. К задаче (вид сверху) |
Ключевым моментом здесь является то, чтобы стена была гладкой. Это означает, что между мячом и стенкой нет трения. Следовательно, единственной силой, приложенной к сфере со стороны стены, является сила упругости, перпендикулярная стене (рис. 4).
 |
| Рис. 4. К задаче |
(Согласно (3):. Вектор изменения импульса оказывается соэкстенсивным с вектором. Это означает, что она перпендикулярна стене в направлении прыгающего мяча (рис. 5).
 |
| Рис. 5. К задаче |
Она равна по модулю вектору (так как скорость шарика не изменилась). Поэтому он представляет собой треугольник, состоящий из векторов и изоклеток. Поэтому угол между векторами равен углу отражения, т.е. фактически равен углу падения.
Обратите внимание, что наш треугольник изоклеток имеет угол (угол падения). Поэтому обратите внимание, что этот треугольник равносторонний. Поэтому:.
Тогда средняя сила, приложенная к сфере, — это то, что мы ищем.
Применение этих законов затруднено, когда оценивается кратковременное взаимодействие объектов. В этом случае для расчета удобнее использовать законы, сохраняющие силу и количество движения.
Импульс силы
Это размер вектора, определяемый типом
Изменение движущей силы тела равно импульсу силы, действующей на тело. Это другая формулировка второго закона Ньютона
Рассмотрим задачу о том, как показать связь между импульсом силы и изменением импульса тела.
Пример. Масса шарика равна 400 г. Скорость, приобретенная шариком после удара, равна 30 м/с. Сила, оказываемая ногой на мяч, равна 1500 Н. Продолжительность удара составляет 8 мс. Найдите силу тяги тела и тягу изменения.

Изменение импульса тела
Как определяется изменение тяги тела? Найдите арифметическое значение импульса сразу, затем найдите импульс через некоторое время. Отнимите первое значение от второго найденного значения. Внимание! Удалите вектор, а не номер. Другими словами, отнимите первый вектор от второго вектора импульса. См. раздел «Удаление вектора».
Пример. Оцените среднюю силу со стороны пола, приложенную к мячу во время удара.
1) Во время удара на мяч действуют две силы: сила опоры и сила тяжести.
Поскольку сила реакции изменяется в течение времени удара, можно найти среднюю силу реакции пола.
2) Изменения импульса тела показаны на диаграмме
3) Из второго закона Ньютона.
Главное запомнить
1) Тип движения тела и импульс силы. 2) Направление вектора импульса. 3) Найдите изменение выталкивающей силы тела.
Момент силы численно равен площади фигуры под графиком f (t).
Если сила не стабильна во времени, например, если F = kt увеличивается линейно, то импульс этой силы равен площади треугольника. Эту силу можно заменить постоянной силой, которая одновременно изменяет импульс тела на ту же величину.
Она равна по модулю вектору (так как скорость шарика не изменилась). Поэтому он представляет собой треугольник, состоящий из векторов и изоклеток. Поэтому угол между векторами равен углу отражения, т.е. фактически равен углу падения.
Импульс тела. Закон сохранения импульса

Эксперименты и наблюдения свидетельствуют, что результат силы (взаимодействия) зависит от времени действия. Например, если один тяжелый груз размещен на нити, к которой снизу присоединена другая нить, и нижнюю нить внезапно потянули, нижняя нить повреждается, но верхняя остается целой. Если нижнюю нить тянуть медленно, верхняя нить оборвется. По этой причине размер используется для описания действия силы, называемой импульсом силы.
Импульс силы — это векторная величина, равная произведению этой силы и времени ее действия ϭ (ϭ vect)ϭ. Силовое давление — это мера действия силы за определенный период времени.
Единица импульса силы равна ⌘ (⌘, F \ cdot t \, ⌘) = 1 Н-с.
2.С другой стороны, действие силы также зависит от свойств тела, к которому эта сила приложена.
Зависимость действия силы от массы объекта можно проиллюстрировать на следующем простом примере. Футбольный мяч, летящий с постоянной скоростью, ударившись о пустую картонную коробку, сдвинется с заданной позиции, но если он ударится о ту же коробку, наполненную металлическими предметами, то легче отскочит назад, а коробка останется неподвижной.
Мяч, летящий со скоростью 2 м/с, ударившись о деревянную стену, в лучшем случае оставит вмятину, тогда как мяч, летящий со скоростью 200 м/с, пробьет стену насквозь. Поэтому действие сил зависит от массы и скорости взаимодействующих объектов.
3. величина, равная произведению массы объекта и его скорости, называется импульсом объекта. \ век
= m \ vec \) — это импульс (или просто импульс) тела. Единицей импульса является ᢙ (ᢙ, p \, ᢙ) = 1 кг -м /с2.
Импульс — это векторная величина, потому что масса — это масштабируемая величина, а скорость — векторная величина.
Импульс является относительной величиной, и его значение зависит от выбора системы отчетности, так же как скорость является относительной величиной. 4.4.
Момент силы и изменение импульса тела взаимосвязаны.
Запишите второй закон движения Ньютона: ǫ (ǫ vec = m \ vec \).
Левая часть уравнения — это импульс силы. Правая часть представляет собой разность между конечным и начальным импульсом тела, т.е. изменение импульса тела. \ vect = \ Delta(m \ vec)\).
Поэтому импульс силы равен изменению импульса тела.
Это еще одна формулировка второго закона Ньютона. Таким образом, Ньютон сформулировал свой закон.
5. тела, взаимодействующие друг с другом, образуют систему тел. Между телами системы действуют взаимодействующие силы. Сила ⌘ (⌘ vec_1 \) действует на одно тело, а сила ⌘ (⌘ vec_2 \) действует на другое тело. В этом случае сила равна и противоположна мощности: \(\ vec_1 =-\ vec_2 \) (рис. 41).
Силы, взаимодействующие с телом системы, называются внутренними силами.
Помимо внутренних сил, на тело системы действуют и внешние силы. Таким образом, взаимодействующие объекты притягиваются к земле. В этом случае гравитация является внешней силой. При движении объектов на них действуют аэродинамические силы и силы трения. А это внешние силы, связанные с системой, которая в данном случае состоит из двух объектов. Ни земля, ни воздух не являются частью этой системы тел.
ПРИМЕРЫ ЗАДАНИЙ
(1) Объект движется с силой 10 Н в течение 5 секунд. Каково изменение импульса тела?
1) 2 Н/с 2) 5 Н-с 3) 50 Н-с 4) Не могу ответить на этот вопрос, потому что масса и скорость объекта неизвестны.
2.Каково значение импульса автомобиля массой 1,5 т, движущегося со скоростью 20 м/с, в системе отсчета, связанной с автомобилем, движущимся в том же направлении и с той же скоростью?
1) 0 2) 15,000 кг-м/с 3) 30,000 кг-м/с 4) 60,000 кг-м/с
3В системе отсчета, относящейся к автомобилю, движущемуся с одинаковой скоростью в противоположных направлениях, каков импульс автомобиля массой 1,5 т, движущегося со скоростью 20 м/с?
1) 0 2) 15,000 кг-м/с 3) 30,000 кг-м/с 4) 60,000 кг-м/с
4. На графике показано изменение скорости велосипедиста с течением времени. Если велосипедист весит 50 кг, каково изменение импульса велосипедиста через 4 секунды после начала движения?
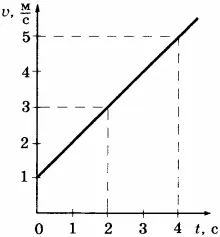
1) 200 кг-м/с 2) 2500 кг-м/с 3) 2000 кг-м/с 4) 2500 кг-м/с
5. тело движется в положительном направлении осевой ɑ (ox \). На этом рисунке представлен график зависимости проекции силы ⌘ (f_x \), действующей на тело ⌘ (t \), от времени. Проекция выталкивающей силы тела на ось между 0 и 5 секундами ߡ (f_x \)

1) уменьшение на 5 кг м/с 2) без изменений 3) увеличение на 10 кг м/с 4) увеличение на 5 кг м/с
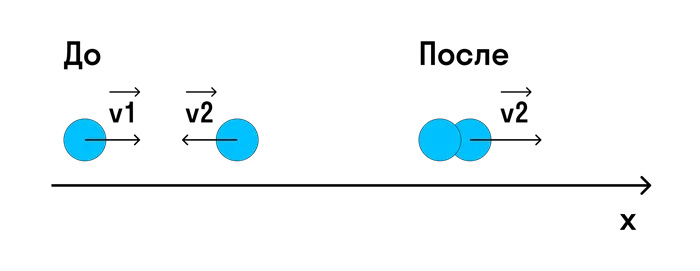
6. два шара массой ⌘(m_1 \) и ⌘(m_2 \) движутся в одном направлении со скоростями ⌘(x_1 \) и ⌘(x_2 \) соответственно на гладком горизонтальном столе (см. форму). Суммарные импульсы сферической системы (p \) равны по модулю

1)ʰ (p = m_2x_2-mx_1 \) и направлен влево, ←2)ʰ (p = m_1x_1-m_2x_2 \) и направлен вправо → 3)←4)ʰ (p = m_1x_1-m_2x_2 \) и направлен вправо →
7. два шарика массами 50 г и 100 г движутся со скоростями 0,6 м/с и 0,4 м/с соответственно. Направление движения сфер образует угол 90°. Мера полного импульса двух сфер равна
1) 0,15 кг-м/с 2) 0,07 кг-м/с 3) 0,05 кг-м/с 4) 0,01 кг-м/с.
8. снаряд, импульс которого равен ⌘ (⌘ vec
\모) он устремился вверх и взорвался на два фрагмента. Импульс фрагментов \(\ vec
_1 \) в момент взрыва был горизонтальным (рис. 1). \Что было направлением импульса ᤩ vec
(_2 \) второго фрагмента) (рис. 2);

9. масса мальчика в три раза больше массы лодки. В момент прыжка с лодки скорость мальчика составляет 1,5 м/с. В то же время лодки получают равные скорости
1) 4,5 м/с 2) 2 м/с 3) 0,5 м/с 4) 0 м/с.
10. сохранение импульса импульс применяется.
é. закрытый b. b в случае любой системы организма.
1) только a) только b 3) и a и b 4) ни a ни b
11. сопоставьте натуральный размер (левая колонка таблицы) с единицей измерения (правая колонка таблицы). Ключ к ответу: напишите выбранное число под соответствующей буквой.
Например, мотоцикл и грузовик с камнями движутся по дороге с одинаковой скоростью. Если грузовик столкнется с забором или другим препятствием, ущерб от грузовика будет гораздо больше, чем от мотоцикла. Это показывает, что понятие «физическое погружение» используется потому, что одной скорости недостаточно для характеристики движения.
Вопрос 8
Физический импульс. Силовой импульс. Закон сохранения импульса.
Краткий ответ.
Толчок тела — это векторная величина, равная произведению веса тела на его скорость.
— Толчок тела, кг-м/с.
Импульс тела направлен в ту же сторону, что и его скорость.
Единицей силы тяги в СИ является 1 кг-м/с.
Натуральная величина, равная произведению силы на ее действие, называется силовым толчком.
Момент силы также является векторной величиной.
Импульс силы равен изменению импульса тела ( II закон Ньютона в импульсной форме ):
Закон сохранения импульса.
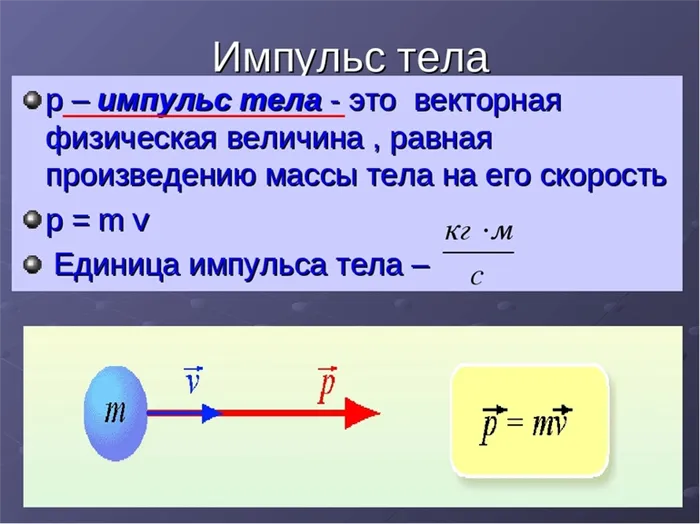
В замкнутой системе векторная сумма импульсов всех тел системы остается постоянной по отношению к взаимодействиям тел этой системы между собой.
1;2 — Скорость тела перед столкновением, м/с
1 ‘,.2 ‘ — скорость тела после столкновения, м/с
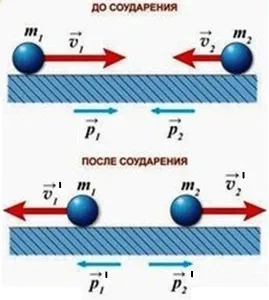
Ответьте на этот вопрос.
Вы когда-нибудь задавались вопросом: ‘ — как скорость тела зависит от его массы и скорости?
- Мяч, летящий с большой скоростью, футболист может остановить ногой или головой, а вагон, движущийся по рельсам даже очень медленно, человек не остановит (масса вагона намного больше массы мяча).
- Стакан с водой находится на длинной полоске прочной бумаги. Если тянуть полоску медленно, то стакан движется вместе с бумагой. а если резко дернуть полоску бумаги — стакан остается неподвижный. (стакан останется неподвижным из-за инерции — явления сохранения скорости тела постоянной при отсутствии действия на него других тел)
- Теннисный мяч, попадая в человека, вреда не причиняет, однако пуля, которая меньше по массе, о движется с большой скоростью (600—800 м/с), оказывается смертельно опасной (скорость пули намного болше, чем мяча).
Поэтому результат взаимодействия тел зависит одновременно от массы тела и его скорости.
Импульс (или количество движения) тела — это векторная величина, равная произведению его массы на его скорость.
— Толчок тела, кг-м/с.
Импульс тела направлен в ту же сторону, что и его скорость.
Единицей силы тяги в СИ является 1 кг-м/с.
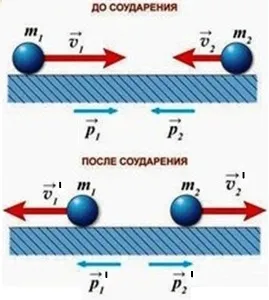
Изменение импульса тела происходит при взаимодействии тел. Когда они сталкиваются друг с другом. Когда тела взаимодействуют, тяга одного тела может быть частично или полностью передана другому телу.
Типы конфликтов:.
Совершенно неупругие удары — это удары, при которых тела совмещаются (слипаются) и движутся как тела.
Пуля прилипает к стержню и движется как тело, плюс кусок пластилина прилеплен к стене
Полный упругий удар — это соревнование, в котором сохраняется механическая энергия системы тела.
После столкновения шарики отскакивают друг от друга в разные стороны. Шары отскакивают от стены.
Предположим, что в течение некоторого короткого промежутка времени на тело массой m действует сила f.
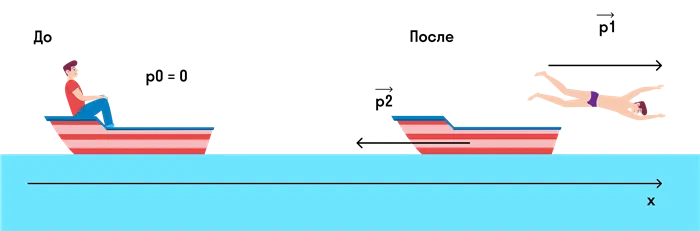
Человек массой m = 45 кг плавает в озере с массой m = 270 кг и решает искупаться. Он останавливает лодку (которая полностью остановилась, чтобы не двигаться) и прыгает с нее с горизонтальной скоростью 3 м/с. С какой скоростью начинает двигаться лодка?
Реактивное движение
Движение некоторых существ, таких как ракеты, фейерверки, кальмары, осьминоги, каракатицы и медузы, основано на законе сохранения импульса. В этих случаях движения тела вызваны разделением частей тела. Это движение называется реактивным движением.
Хорошим примером приведения в движение с помощью реактивного топлива в технике является движение ракеты, когда из ракеты вылетает струя газа, образующаяся в результате сгорания топлива.
Сила, действующая со стороны ракеты на газ, равна метру и противоположна силе, с которой газ отталкивает ракету от себя.
Эта сила называется реактивной силой. Это сила, возникающая при разъединении частей тела. Особенностью реактивной силы является то, что она возникает без какого-либо взаимодействия с внешним телом.
Закон сохранения импульса позволяет оценить скорость ракеты.
Это позволяет выразить скорость ракеты в виде:.
Скорость ракеты в реактивном движении.
Этот тип относится к случаю мгновенного сгорания. Мгновенное горение — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.








