Гармонические колебания. Какие колебания называются гармоническими?

это настоящая гармоника колебание. Таким образом, гармоника колебания можно записать в комплексной форме (7) и выполнить все необходимые вычисления. При выводе результата необходимо взять действительную или мнимую часть, чтобы получить физические величины.

Колебательное движение

Колебательное движение (колебание) — это любое движение или изменение состояния, которое повторяется во времени или повторяются значения физических величин, характеризующих это движение или состояние.

Различные физические явления являются колебания: звуковые колебания, электромагнитные, механические и т.д. Общими для всех этих явлений являются законы и математические методы, с помощью которых они описываются.

Колебательное движение называется периодический, когда переменные этого колебаний повторять через равные промежутки времени.

Колебания называются Свободные, когда они возникают в системе, в которой не действуют внешние силы (или их действие взаимно компенсируется).

Такая система удаляется от состояния равновесия. Когда колебательная система консервативна, потери энергии составляют при колебаниях отсутствует. В этом случае свободный колебания амортизируется. Свободный без демпфирования колебания, возникающие под действием упругих сил, являются гармоническими.

Продолжительность затухания колебаний называют минимальный интервал времени ($T$), после которого значения всех физических параметров, обозначаемых через колебание.

Частотой колебаний ($\nu $) называют обратная величина периода колебаний, количество полных колебаний, колебаний, производимых колебательной системой:

Гармонические колебания

Самым простым типом колебаний считаются гармоничными колебания.

Колебания называют Гармонический, если изменение физического параметра описывается законом синуса или косинуса.

Если мы позволим гармонике колебания параметра $s$, тогда описывается следующим образом как:

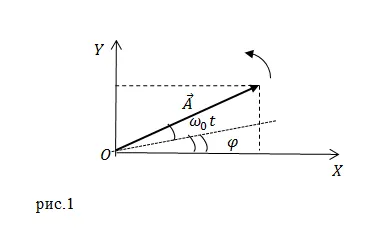
где $A=s_$ — амплитуда колебаний (постоянная во времени); $<\omega >_0$ — циклическая (циклическая) частота колебаний (не зависит от времени) — $\varphi$ — начальная фаза колебаний (фаза при $t=0$); $(<\omega >_0t+\varphi )$ является фазой колебаний. Значение $s$ изменяется $-A\le s\le 3500A.

Те же самые колебания можно описать как:

В течение периода, соответствующего колебаний поэтому фаза изменяется на величину 3500\pi$:

Циклическая частота $<\omega >_0$ равно количеству полных циклов колебаний, которую совершает колебательная система за 3500\pi$:

Дифференциальное уравнение колебательного движения

Линейное дифференциальное уравнение гармонического колебаний это выражение:

Решениями уравнения (6) являются выражения (2) и (3). Уравнение вида (6) называют уравнение гармонического осциллятора и колебательной системы, которое является эти колебания гармонический осциллятор (примерами гармонических осцилляторов являются: Пружинный маятник, естественный маятник, электрический колебательный контур).

Это уравнение эллипса, оси которого произвольно ориентированы относительно координатных осей. Ориентация эллипса и величина его полуосей зависят от амплитуд колебаний и разность фаз.

Содержание

• Свободные колебания осуществляются внутренними силами системы после того, как система отошла от положения равновесия, как система выводится из состояния равновесия. Вокруг бесплатно колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание).
• Вынужденные колебания выполняются под воздействием внешней периодической силы. Для того чтобы колебательная система была гармонической, достаточно, чтобы она была линейной (описывалась линейными уравнениями движения) и чтобы сама внешняя сила изменялась со временем. как гармоническое колебание (то есть чтобы зависимость от времени этой силы была синусоидальной).

Применение

Гармонические колебания можно отличить от всех других типов колебаний по следующим причинам:

• Очень часто 2 малые колебания, как свободные, а также вынужденные, которые возникают в реальных системах, могут рассматриваться как гармоники. колебаний Категория периодических функций может быть разложена на сумму тригонометрических компонентов. Другими словами, каждый колебание может быть представлена как сумма гармонических колебаний.
• Для широкого класса систем откликом на гармоническое воздействие является гармоническое колебание (свойство линейности), а соотношение между воздействием и реакцией является постоянным свойством системы. Ввиду вышеупомянутого свойства это позволяет изучить прохождениеколебаний произвольной формы через системы.

См. также

1. ↑ То есть не равное тождественно нулю.
2. ↑ Подразумеваемым условием здесь является то, что свойства системы должны быть постоянны во времени (что в реальности достаточно часто выполняется, по крайней мере, приближенно).

• Физика. Элементарный учебник физики / Под ред. Г. С. Лансберга. — 3 изд. — М ., 1962. — Т. 3.
• Хайкин С. Э. Физические основы механики. — М ., 1963.
• А. М. Афонин. Физические основы механики. — Изд. МГТУ им. Баумана, 2006.
• Горелик Г. С. Колебания и волны. Введение в акустику, радиофизику и оптику. — М .: Физматлит, 1959. — 572 с.

• Викифицировать список литературы, используя шаблон >, и проставить ISBN.
• Проставив сноски, внести более точные указания на источники.
• Добавить иллюстрации.

Фонд Викимедиа. 2010.

Полезное

Смотреть что такое «Гармонические колебания» в других словарях:

АРМОНИЧЕСКИЕ ДОМИНАЦИИ — АРМОНИЧЕСКИЕ ДОМИНАЦИИ, периодические изменения физической величины, происходящие по закону синусов. Графическое представление гармонического колебания колебания Гармоническое колебание обозначается синусоидальной кривой. Гармонический колебания Простейший тип периодического движения, характеризующийся … Современная энциклопедия

Гармонические колебания — ГАРМОНИЧЕСКИЕ ВИБРАЦИИ, периодические изменения физической величины, происходящие по закону синусоиды. Графически, гармонический колебания Гармоническое колебание обозначается синусоидальной кривой. Гармонический колебания Простейший тип периодического движения, характеризующийся … Иллюстрированный энциклопедический словарь

Гармонические колебания — Колебание, при котором физическая величина изменяется со временем в соответствии с законом синусов или косинусов. Графически H. c. представлена кривой синуса или косинуса (см. рисунок); она может быть записана в следующем виде: x = Asin (ωt + φ) или x … Большая советская энциклопедия

АРМОНИЧЕСКИЕ ДВИЖЕНИЯ — АРМОНИЧЕСКИЕ ДВИЖЕНИЯ, периодическое движение, как. как Движение МАЯТНИКА, атомарное. колебания или колебания В цепи. Тело воспроизводит незатухающие гармоники колебания, когда он колеблется вдоль линии и движется равномерно … … научно-технический энциклопедический словарь

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ — колебания, Когда физическая (или другая) величина изменяется синусоидально со временем: x=Asin(wt+j), где x — значение колеблющейся величины в данный момент времени t (для техники, например, короткое. G. c., например, перемещение или скорость, для … … Энциклопедия физики

гармонические колебания — Механические колебания, Когда обобщенные координаты и/или обобщенная скорость изменяются пропорционально синусу с аргументом, линейно изменяющимся со временем. Сборник рекомендуемых терминов. Выпуск 106. технология. колебания. Академия наук … Руководство для технических переводчиков

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ — колебания, В котором физическая (или другая) величина изменяется синусоидально со временем, x — значение величины, колеблющейся в момент времени t (в технических единицах измерения, например, перемещение и скорость или напряжение и сила тока в электрических аппаратах) … Энциклопедия физики.

АРМОНИЧЕСКИЕ ДВИЖЕНИЯ — (см.), при которых физическая величина изменяется во времени по закону синусов или косинусов (например, перемещение и скорость). при колебании (см.) или изменения (см.) и ток в электрической Г. с.) … Большая техническая энциклопедия

Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость составляют 0,05 м и 0,12 м/с соответственно. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.

Колебания в природе

Различные колебания Это все вокруг нас. Большинство движений в природе, даже направленных, имеют хотя бы небольшой колебательный компонент.

Рисунок 1: Колебания в природе.

Среди колебаний Различают периодические (волны, маятник) и непериодические (шлейф на ветру). Основное различие между ними заключается в том, что каждый периодический колебание по своим характеристикам очень похожа на предыдущую и последующую. Исследование непериодических колебаний показывает, что каждый из них может быть представлен бесконечной суммой периодических значений колебаний. Поэтому описание любого колебательного процесса на основе описания периодических колебаний.

Гармонические колебания и их закон

Изучение колебаний следует начинать с построения его диаграммы. Время $t$ откладывается по оси абсцисс, а отклонение $x$ — по оси ординат. Используется маятник с песком или цветным порошком, а также его колебания, лист бумаги расстилается под ним так, чтобы след от

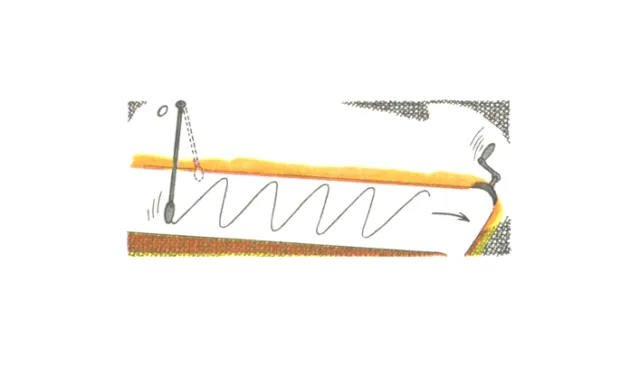
Рис. 2. Запись колебаний маятника.

Вкратце напомним, что причинойколебаний маятника является равновесие, которое равно нулю в среднем и максимальному в крайних положениях и устанавливается во время отклонения. Ускорение маятника при этом не меняется.

Теория высшей математики доказывает, что единственной функцией, ускорение которой пропорционально прогибу и направлено во время прогиба, является кривая синуса $x=A sin(\omega t+\phi)$.

Если вы посмотрите на след маятника на листе, который вы тянете, вы увидите кривую, которая является как раз этой функции.

Колебания подчиняются закону синусов, называются гармоническими колебаниями. Параметр $A$ в приведенных выше формулах называется это амплитуда, параметр $\omega$ — частота (иногда циклическая частота), параметр $\phi$ — фаза (иногда начальная фаза). Хорошие примеры гармоник колебаний это также волны на воде, движение груза на пружине и движение поршня в двигателе автомобиля.

Параметры гармонического колебания

Формула для гармоники колебания имеет три параметра.

• Амплитуда $A$ описывает «амплитуду». колебания. Разность амплитуд колебаний (при прочих равных) означает разность наибольшего отклонения, которое наблюдается у исследуемых явлений. Маятник с большей амплитудой будет качаться на большее отклонение, хотя пройдет точку равновесия одновременно с маятником, у которого амплитуда меньше.
• Частота $\omega$ описывает «скорость». колебания. Разница в частоте означает разницу в количестве колебаний в единицу времени (при прочих одинаковых условиях). Достаточно маятника с вдвое большей частотой. два колебания за время одного колебания другого маятника, хотя амплитуда при этом будет одинакова.
• Фаза $\phi$ описывает «положение в начальный момент времени». Разность фаз означает, что рассматриваемые процессы находятся в разных состояниях в одно и то же время, a колебание Одна проходит через точку равновесия, а другая находится в точке максимального отклонения в этот момент. Маятники с разными фазами (при одинаковых условиях) отклоняются на одну и ту же величину, а число колебаний за одно и то же время у них будет одинаково. Но при этом они всегда будут в разных состояниях, один маятник будет постоянно «догонять» другой.

Определение «гармонический для колебаний возникла в древности в результате изучения музыкальной гармонии, когда стало ясно, что движение вибрирующей струны может быть хорошо описано законом синуса.

Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость составляют 0,05 м и 0,12 м/с соответственно. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.

Применение маятников

Чтобы вычислить энергию гармоники колебаний На практике используются различные приборы, в том числе осциллятор. Он представлен в виде математического маятника со специальной механической системой. Последние элементы находятся в состоянии невесомости, в однородном гравитационном поле. Период незначительной вертикали колебаний не зависит от амплитуды. Он рассчитывается по следующей формуле.

Если для эксперимента используется физический маятник, то твердое тело смещается в поле определенных сил относительно материальной точки, которая не является центром масс тела. Если рассматривается фиксированная ось, колебания перпендикулярны направлению сил и не проходят через центр масс тела. В определенные моменты значение равно нулю или достигает максимального значения.

Чтобы определить величину стоячей волны, мы должны учесть следующее колебания в системе с узловой амплитудой. Аналогичное явление наблюдается при отражении волн от препятствия. При расчете учитывается количество фаз, частота и коэффициент затухания волны в точке отражения. Аналогично колебания генерируется струнами, воздухом в трубе.

В среде также существуют волны потока, которые приносят энергию к точкам излучения/поглощения. При проектировании генерации движения в электромагнитном поле учитываются свойства рассматриваемой волны.

Процесс считается последовательным. Он тесно связан с вектором напряжения, магнитным полем. В то же время магнитное поле изменяется, вызывая колебания в электрическом поле. Для теоретического описания физических явлений используется монохроматическая волна.

Разница в этой модели заключается в том, что в спектр включается только один компонент частоты волны:

• строго гармоническая;
• имеет постоянную частоту;
• имеет начальную фазу;
• имеет амплитуду.

Рассеяние света также характеризуется ГК. В процессе рассеяния света участвуют фазовые скорости и преломление в абсолютных значениях. Теория была открыта Ньютоном в 1672 году.

Классификация системы

Свободные колебания осуществляются внутренними силами системы после ее выхода из состояния равновесия. Для того чтобы движения были гармоничными, необходимо описать линейное уравнение. В системе отсутствуют потери энергии. При его ненулевом значении в системе после возбуждения возникает демпфирование.

Вынужденные движения происходят под воздействием внешней силы, но имеют периодический характер. Для того чтобы процесс был гармоничным, колебательная система должна быть линейной. В этом случае внешняя сила может периодически колебаться. как гармоническое колебание. В этом случае временная зависимость силы имеет синусоидальный характер.

Небольшие вынужденные и свободные МБ часто встречаются в реальных системах. Они могут принимать форму стандартных колебаний или близко к этому. В 1822 году Фурье открыл широкий класс периодических функций, которые могут быть разложены на сумму их тригонометрических компонентов. Ряд Фурье формируется таким образом.

В соответствии с этим, каждое периодическое движение представляется как сумма ГЦ с соответствующими амплитудами, начальными фазами и частотами. Члены этой суммы включают гармонические колебание, характеризуется минимальной частотой. Она называется основной. Само колебание считается основной гармоникой или основным тоном. Частоты других членов, GC, кратны основной частоте.

Такие колебания называются Частоты других членов кратны основной частоте. Они могут быть первичными или вторичными. Устройства, работающие по этому принципу, обладают свойством линейности. Ученые обнаружили взаимосвязь между эффектом и реакцией, что называется постоянное свойство системы. Эта информация позволяет исследовать прохождение смещений, скачков, произвольных колебаний.

Когда в задаче используется ускорение свободного падения, считается, что g — постоянная величина. Она равна 9.8. В зависимости от неизвестных величин, заданных параметров, применяются другие формулы.

Практические пособия издаются по отдельным темам, разделам физики. Так как Уравнение следует графику синуса или косинуса, поэтому практические занятия включают математические упражнения. Некоторые координаты обозначены конкретными значениями. Уравнение решается всеми возможными математическими способами.

Начальное смещение груза не является амплитудой, так как вместе с начальным смещением, скорость, с которой воспринимается нагрузка. Однако полная энергия может быть выражена через амплитуду колебаний:

5. Пружинный, математический и физический маятники.

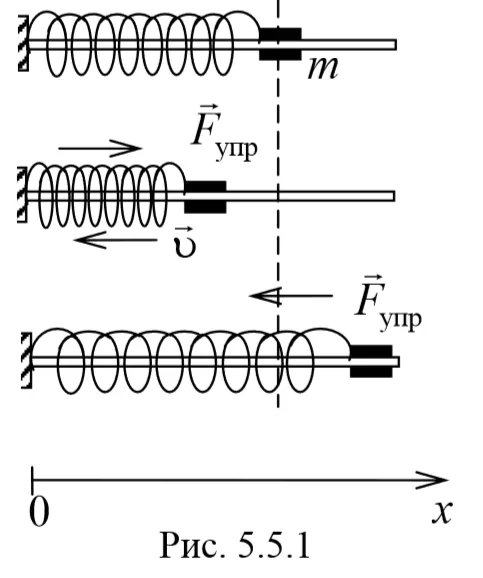
Рассмотрим некоторые более простые системы, генерирующие свободные гармоники колебания.

1) Маятниковая пружина — это материальная точка массой m, подвешенная (или расположенная горизонтально) к идеально упругой пружине жесткостью k и производящая гармонические колебания. колебания под действием упругой силы. Предположим, что шар массой m, прикрепленный к пружине, совершает работу колебания. Чтобы составить дифференциальное уравнение колебаний запишем второй закон Ньютона для движения в проекции на ось Ox F_.=ma Сила упругости F_.= Приравнивая два последних уравнения и применяя определение ускорения, получаем

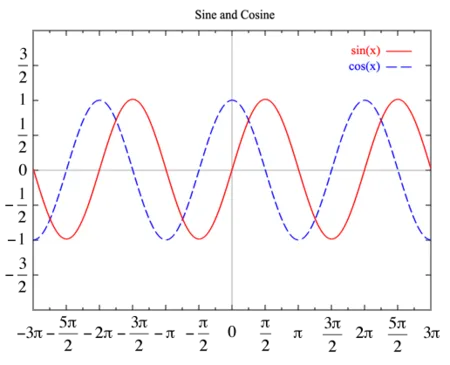
Из сравнения уравнений (5.3.7) и (5.5.2) следует, что маятниковая пружина производит гармоники колебания с частотой

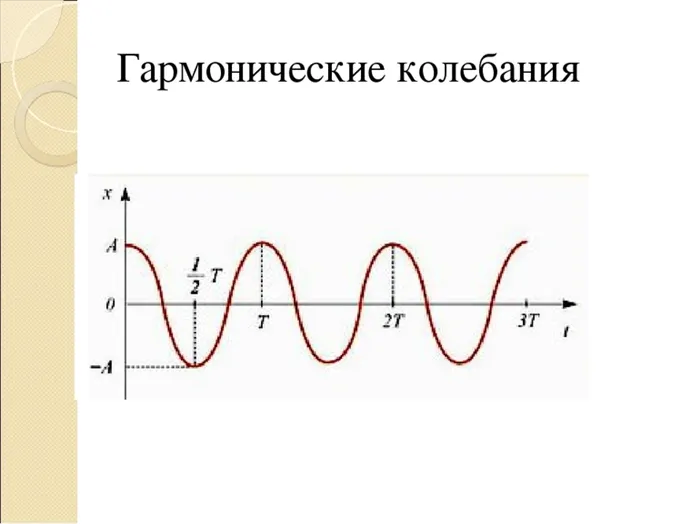
Так как период колебаний определяется формулой T= $2π\over ω_0$, тогда период равен колебаний пружина маятника

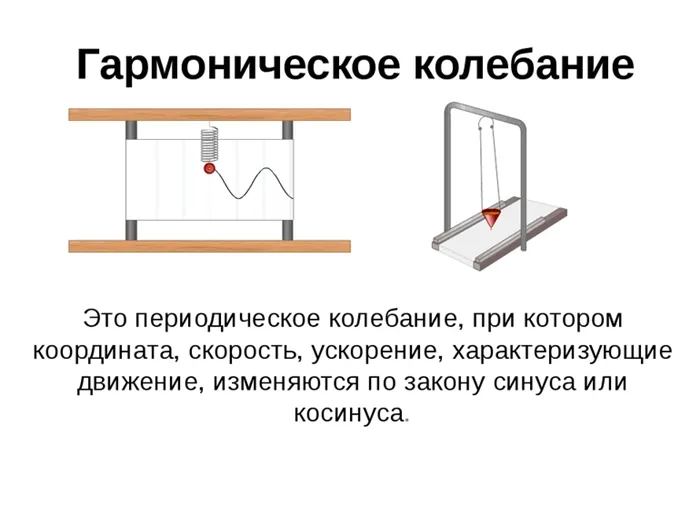
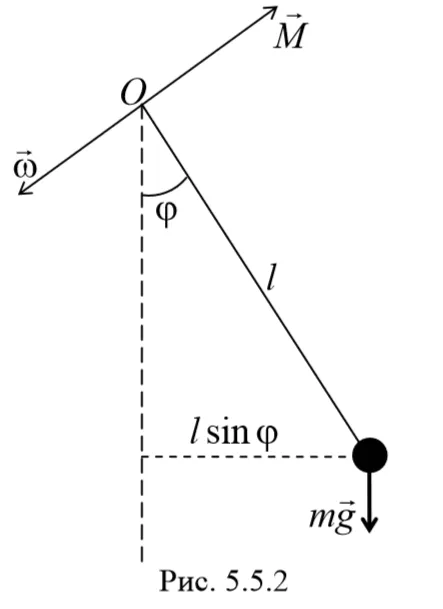
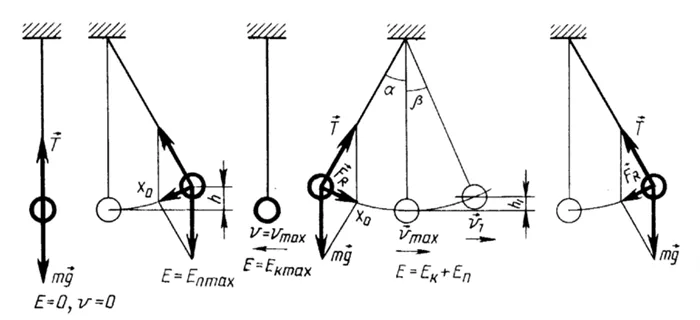
2) Математический маятник — это идеализированная система, состоящая из невесомой и нерастяжимой нити, к которой подвешена материальная точка массой m. Отклонение маятника от положения равновесия характеризуется углом φ, который образует струна с вертикалью.

Когда маятник отклоняется от положения равновесия, возникает момент M, который равен mqlsinφ и имеет то же направление, что и момент, возвращающий маятник в положение равновесия. Таким образом, выражение для крутящего момента: M = mqlsinφ. Давайте применим основной импульс

где L=ml 2 — момент инерции материальной точки. Поскольку угловое ускорение равно ε= $d^2φ\over dt^2$, получаем.

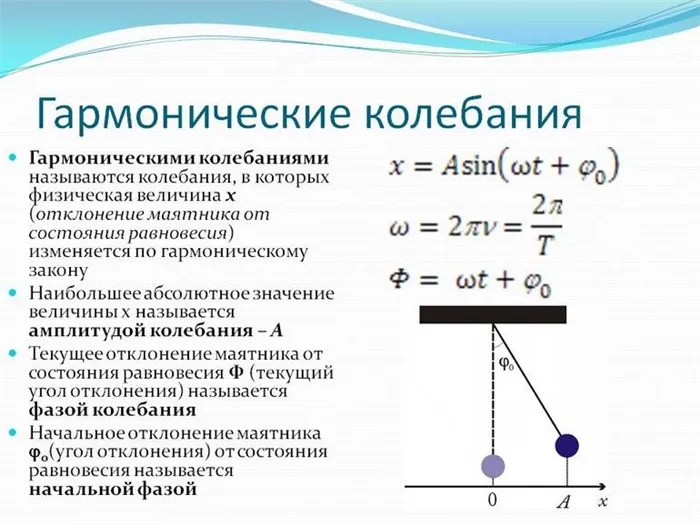
Если у нас есть небольшие колебания, тогда sinφ≈φ. Получаем

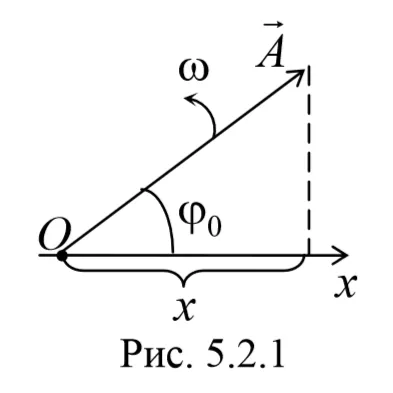
То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой

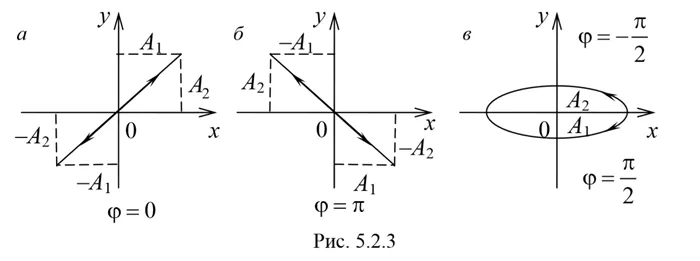
Период колебаний математического маятника

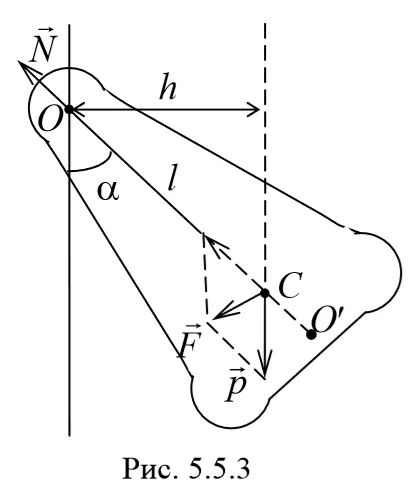
3) Физический маятник — это жесткое тело, которое под действием силы тяжести движется колебания вокруг неподвижной оси, проходящей через точку, не совпадающую с центром масс тела. Если маятник отклоняется от положения равновесия на угол φ, возникает вращающий момент, который заставляет маятник вернуться в положение равновесия. Этот импульс равен M=-mglsinφ .

Согласно основному уравнению динамики вращательного движения, действует следующее

где I — момент инерции маятника относительно оси, проходящей через точку подвеса.

Если у нас есть небольшие колебания, тогда sinφ≈φ. Получаем

То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой

ГАРМОНИЧЕСКИЕ колебания — это периодические колебания. колебания, изменение во времени физической величины происходит по закону синуса или косинуса (см. рис.): s = Asin(wt+f0), где s — отклонение колеблющейся величины от ее среднего значения (равновесия), A=постоянная амплитуда, w=постоянная циклическая … Большой энциклопедический словарь техники

Описание графика, применение маятников

Гармонические колебания имеют важную характеристику, а именно тот факт, что период колебаний не зависит от их частоты. В качестве моделей для демонстрации гармоник. колебаний используются:

• пружинный маятник;
• математический маятник.

Предположим, что восстанавливающая сила — это сила упругости, определяемая по формуле:

Где x — отклонение от положения равновесия,

k — коэффициент эластичности.

Согласно второму закону Ньютона:

Деление полученного уравнения на массу дает выражение для определения ускорения вибрирующего тела:

Если известна угловая частота, то в соответствии со вторым законом Ньютона можно определить линейную частоту или период. колебаний можно рассчитать следующим образом:

Угловая частота для математического маятника может быть определена аналогичным образом. Кроме того, к колебательным движениям применим закон сохранения энергии.

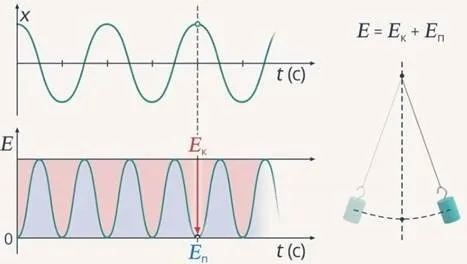
Колебательное движение маятника, которое является гармоническим, может быть вызвано двумя способами. В первом случае вес поднимается из положения равновесия, а затем отпускается. Это движение графически показано на рисунке.

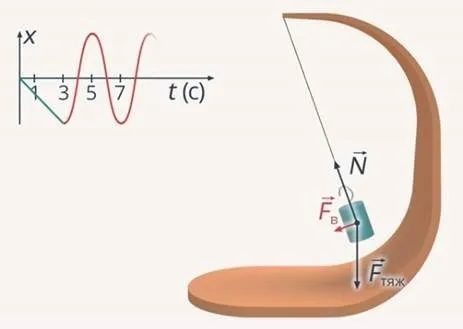
Второй метод — дать телу толчок, после чего оно производит гармоники. колебания. Например, можно толкнуть предмет или сдвинуть качели, сначала выведя их из положения равновесия, а затем отпустив. При каждом промежуточном значении маятника сумма кинетической и динамической энергии равна начальной энергии маятника.

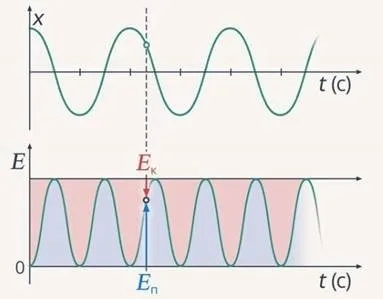
В действительности не существует маятников, которые могли бы качаться долгое время. Такая ситуация является абстрактной.

Маятниковая система не является замкнутой из-за силы трения. Действие этой силы способствует потере энергии при колебательных движениях маятника.

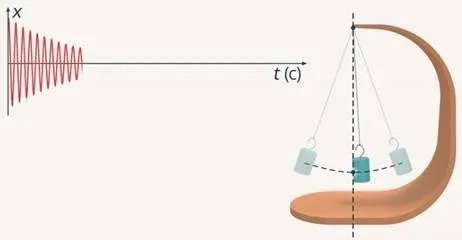
Сила трения может быть внешней или внутренней. В первом случае это окружающий воздух или другая среда. Внутренняя сила может находиться в подвесе маятника.

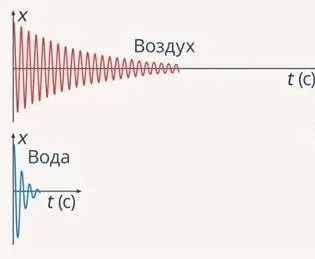
В результате амплитуда будет колебаний быть уменьшены. В конечном итоге это приведет к остановке маятника. В то же время колебания он будет затухать.

Какое уравнение выражает смысл гармонического колебания

Согласно определению, гармоникаколебания имеют кинематические свойства, которые изменяются по закону синуса или косинуса.

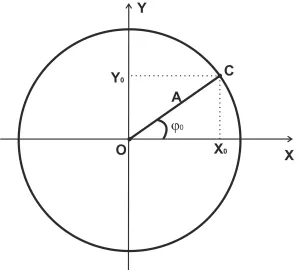
Для визуализации гармоники колебания можно представить как вращательное движение как колебательное движение вдоль двух осей, перпендикулярных друг другу. Предположим, что тело вращается по окружности радиуса A. Его начальное положение совпадает с точкой C. В начале движения радиус-вектор, описывающий эту точку, образует угол \(\varphi _\) с осью OX.

Начальные координаты могут быть вычислены из проекций радиуса на ось:

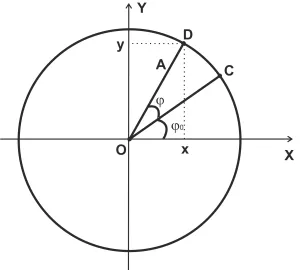
Можно предположить, что тело, имеющее угловую скорость \omega, переместилось в точку D через время t. Угол поворота равен \(\varphi _\). В этом случае угол поворота радиус-вектора относительно начального положения равен \(\varphi.\) Текущие координаты тела одинаковы:

\(x=A\cos(\varphi +\varphi _)\)

\(y=A\sin (\varphi +\varphi _)\)

Если это равномерное движение тела по окружности, то:

\(x=A\cos (\omega*t +\varphi _)\)

\(y=A\sin (\omega*t +\varphi _)\)

Записанные уравнения представляют собой закон движения материальной точки, которая является гармошкой колебания по контуру. Если \(\sin (90^-\alpha )=\cos \alpha,\), то уравнение можно преобразовать следующим образом:

\(x=A\cos (\omega*t +\varphi _)=A\sin (\omega*t-90^ +\varphi _)=A\sin (\omega t+\varphi ^_)\)

где \(\varphi ^_ = \varphi _-90^\) — новый параметр, характеризующий другое начальное положение тела.

Из представленных закономерностей следует, что записанные уравнения теоретически одинаковы при различных начальных условиях. В качестве примера можно проанализировать только первое уравнение. Каждый из представленных параметров, имеющий свой аналог во вращательном движении, по-разному описывается в колебательном движении:

\(x=A\cos (\omega*t +\varphi _)\)

x — текущая координата тела,

А — это амплитуда колебаний (максимальное отклонение тела от положения равновесия),

\(\omega\) — циклическая частота колебания;

t — время движения,

\(\varphi _)\) — представляет собой начальную фазу колебания;

\(\omega*t +\varphi _)\) — текущая фаза колебания (все под тригонометрической функцией).

Имея информацию об общей форме колебательного движения, мы можем определить зависимость скорости и ускорения от времени:

\(x=A\cos (\omega*t +\varphi _)\)

\(v_=-A\omega \sin(\omega*t +\varphi _)\)

где \(v_\) — скорость тела, а \(a_\) — его ускорение.

Это уравнение является основным гармоническим уравнением колебаний, которые часто встречаются при решении проблем.

Применение гармонических колебаний в жизни

Колебания часто встречаются в природе и в технике. Как и вращение, колебательные процессы являются основой для развития таких отраслей, как электротехника и радиотехника. Часто колебания оказывают негативное влияние. Например, крылья самолетов, корпуса кораблей, здания и сооружения колеблются из-за резонанса используемого там оборудования. Это учитывается инженерами в таких проектах.

Вибрации используются при изготовлении музыкальных инструментов. Например, струны вибрируют под руками музыканта, что приводит к колебания и окружающие слышат музыку.

Многие важные внутренние процессы в человеческом организме связаны с вибрациями. Например, человеческое сердце в состоянии покоя совершает около одного колебательного движения в секунду. Повторяющиеся нервные импульсы вызывают постоянные сокращения и растяжения мышц. Люди могут слышать и говорить благодаря колебаниям.

Свет также имеет вибрационную природу. Кроме того, люди также совершают вибрационные движения. Гармонический колебания токи активно используются в производстве технических устройств.

Гармонические сигналы в диапазоне от долей Гц (сверхнизкие частоты) до десятков или сотен ГГц (сверхвысокие частоты) широко используются в радиотехнике и телекоммуникациях. Разнообразные звуки и изображения передаются на большие расстояния с помощью электромагнитных волн.

Электромагнитные волны генерируются при наличии высокочастотного переменного тока с определенным напряжением, подаваемого на передатчик, а электронные генераторы, входящие в конструкцию радиопередатчика, используются для генерации высокочастотного переменного тока.

Гармонические сигналы в диапазоне от долей Гц (сверхнизкие частоты) до десятков или сотен ГГц (сверхвысокие частоты) широко используются в радиотехнике и телекоммуникациях. Разнообразные звуки и изображения передаются на большие расстояния с помощью электромагнитных волн.

Основные параметры гармонических колебаний

a) период колебания

б) частота колебания

Единица измерения c) циклическая частота секунд:

Из формул (5.5) и (5.6) следует гармоническое уравнение колебаний (5.2) можно записать в следующем виде.

Большинство величин, используемых для количественной оценки гармоник колебания, смещения изменяются со временем по закону синуса или косинуса (скорость, ускорение, кинетическая и потенциальная энергия), также изменяются гармонически. Это подтверждается следующими диаграммами и уравнениями:

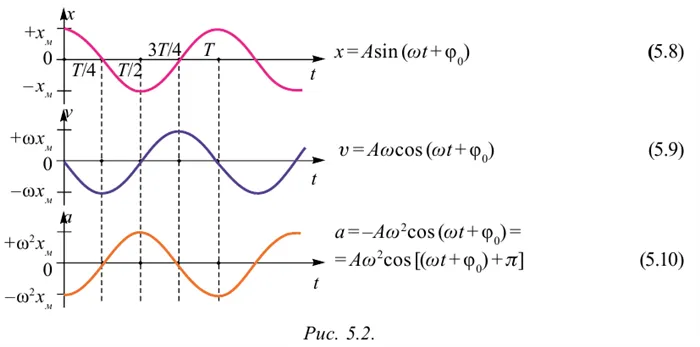
Пример решения проблемы:

Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость составляют 0,05 м и 0,12 м/с соответственно. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.

Формула и решение:

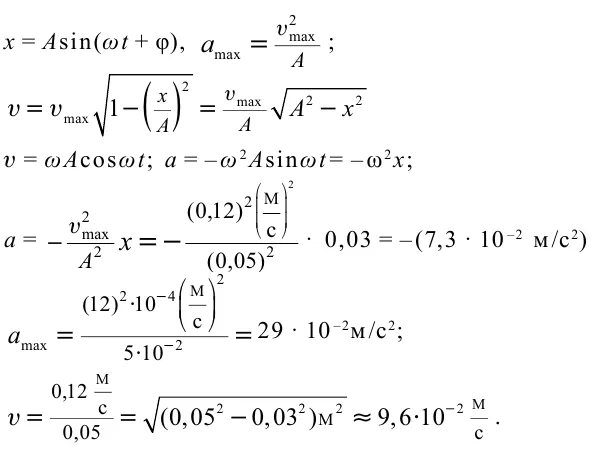
Гармонические колебания пружинного маятника

В 1985 году Мехико пострадал от страшного землетрясения: 5 526 человек погибли, 40 000 человек получили ранения, а 31 000 человек остались без крова. Исследования показали, что основной причиной катастроф во время землетрясения является совпадение частоты разрывов колебаний зданий с частотой принудительной эвакуации из них колебаний земля. Поэтому при строительстве новых зданий в сейсмоопасном районе важно, чтобы эти частоты не совпадали. Это может уменьшить последствия землетрясения. Для этого важно знать, от чего зависят частота и период. колебаний.

Одна из простейших колебательных систем, генерирующих гармоники колебания, это пружинный маятник.

Пружинный маятник — это колебательная система, состоящая из пружины и соединенного с ней тела. Колебания пружинного маятника являются гармоническими. колебаниями:

Под гармоническими колебаниями подразумеваются колебания, Они возникают в результате действия силы, которая прямо пропорциональна перемещению и направлена в направлении движения.

Исследование колебаний Колебания пружинного маятника имеют большое практическое значение, например, для расчета колебаний При исследовании воздействия маятниковой пружины на фундаменты зданий и тяжелых станков колебаний на фундаментах зданий и тяжелой техники, при определении упругости ушных мостиков в диагностике ЛОР-заболеваний. колебаний маятниковой пружины является актуальной проблемой.

Для уменьшения количества сил, действующих на колебательную систему, рекомендуется использовать горизонтально установленную колебательную систему с пружинным шариком (d).

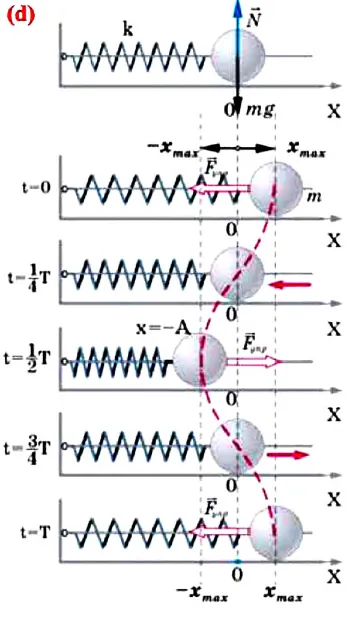
В этой системе силы тяжести и реакции опоры взаимно уравновешивают друг друга. Если шар вывести из состояния равновесия, например, растянув пружину в

Формула (4.9) представляет собой уравнение свободной гармоники колебаний маятниковой пружины.

Здесь — проекция ускорения сферы вдоль оси — удлинение пружины, которое равно амплитуде колебания. Для данной колебательной системы коэффициент равен квадрату циклической частоты

Поэтому уравнение движения пружинного маятника можно записать следующим образом:

Уравнение (4.12) показывает, что колебания маятниковой пружины с циклической частотой

Так как тригонометрическая функция является гармонической функцией, тогда и колебания пружина маятника является гармонической колебаниями.

Гармонические колебания математического маятника

Такая историческая информация дошла до наших дней: В 1583 году итальянский ученый Г. Галилей наблюдал колебания люстры, висящей на длинном тросе в храме в Пизе. Он, сравнивая люстру колебания люстры на свой собственный пульс и заметил, что, несмотря на уменьшающуюся амплитуду колебания, время, необходимое для полного колебание (период колебания) люстры не изменилось. Затем Галилей провел многочисленные исследования для определения периода и частоты маятника, изменяя длину маятника с нитью, вес подвешенного к нему груза и высоту положения маятника (по сравнению с уровнем моря). колебаний маятника.

Гармонические колебания Период и частота маятника также зависят от силы тяжести. Это можно наблюдать с помощью математического маятника.

Математический маятник — это идеализированная колебательная система, состоящая из материальной точки, подвешенной на невесомой и ненатянутой струне.

Для исследования колебаний Система, состоящая из тонкой длинной струны и сферы (b), может быть использована в качестве математического маятника.

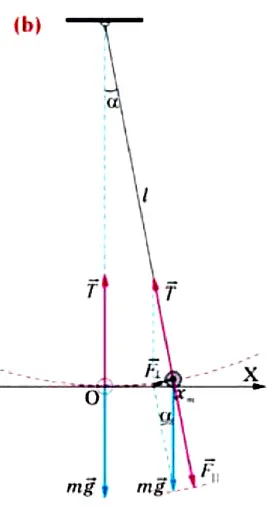
Однако если мы выведем маятник из равновесия, переместив его на небольшой угол и перпендикулярно струне, гравитация и гравитационная составляющая «попытаются» вернуть тело в положение равновесия (см.: рис. b ). Учитывая вышесказанное и ссылаясь на II закон Ньютона, мы можем составить уравнение для колебательного движения тела с массой OX:

Учитывая:

Для уравнения движения математического маятника получаем:

Где находится ускорение свободного падения?

Для этой колебательной системы отношение также соответствует квадрату циклической частоты

Таким образом, уравнение движения математического маятника можно записать следующим образом:

Уравнение (4.19) показывает, что колебания математического маятника является гармоническим колебаниями (4.4) Уравнение (4.4) показывает, что математический маятник имеет угловую частоту с циклической частотой. Из математики известно, что решением этого уравнения является следующая функция:

Так как эта функция является гармонической, тогда и колебания математического маятника является гармоническим колебаниями.

Из этого мы определяем величины, на основе которых период и частота колебаний математического маятника: