Системы счисления в информатике: виды, примеры, характеристики. Что такое системы счисления

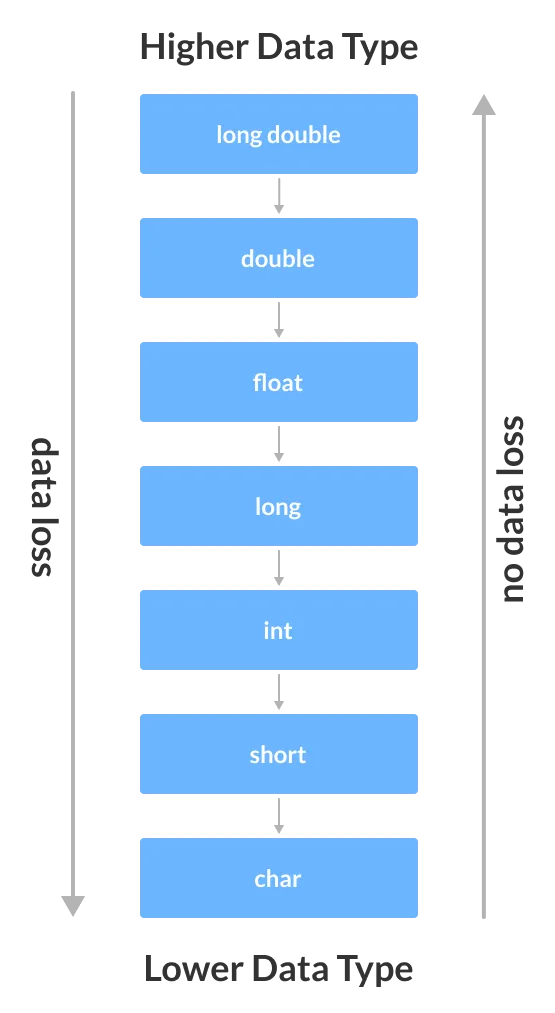
Примером может служить 101. Это аналогично числу 5 в десятичной системе счисления. Для преобразования из 2 в 10 каждый разряд двоичного числа должен быть умножен на основание ‘2’. Она увеличивается на величину, равную одной цифре. Таким образом, число 101₂ = 1*2 2 + 0*2 1 + 1*2 0 = 4 + 0 + 1 = 5₁₀.

Системы счисления в математике

Система нумерации — это набор правил для записи чисел с помощью конечного набора символов (цифр). Системы нумерации могут быть непозитивными (в таких системах значение номера не зависит от его местоположения — его местоположение находится в количестве регистраций).

Неравномерность. Системы нумерации — это числовые системы, в которых каждая цифра имеет фиксированное значение независимо от ее расположения.

Примером неположительных обозначений, которые используются и сегодня, являются римские цифры. В этой системе для записи чисел используются следующие цифры: I, V, X, C, D, M и т.д. Другие числа описываются специальными правилами. Множество соседних одинаковых чисел представляют собой числовые значения, равные сумме числовых значений, соответствующих этим числам. III — 3, а xx — 20; одиночная цифра (представляющая меньшее число) слева от большей цифры (представляющей большее число) представляет собой разность между соответствующими числами. IV — 4, а XL — 40. Это цифра числа справа от старшего разряда, которая представляет собой сумму соответствующих чисел. Xi — 11, VI — 6 и т.д. п.

Система позиционирования

Положение. Система нумерации, в которой значение каждого числа определяется не только самим числом, но и местом, которое оно занимает в числовом регистре, называется позиционной.

База. позиционной системы счисления называется число будем обозначать через

Система позиционирования на основе различных целых чисел.Система, основанная на Система нумерации. Существует различие между тоталитарной базой и симметричной позицией. В полном числе цифра представляет собой непрерывное целое число, начинающееся с нуля в нулевой системе, в симметричной базовой системе позиционирования. Цифра представляет собой непрерывное целое число, расположенное симметрично вокруг нуля и нуля. Обычно позиционная нотация ноль и один означает нулевое число и единицу.

Цифры системы нумерации, разделенные запятыми на целую и дробную части. Если для представления чисел в системе используются буквы, то последовательность чисел такова.

Числовые операции над числами в системе нумерации подчиняются тем же правилам, что и в таблице дробей. Однако, если действие выполняется с использованием чисел в какой-либо системе, необходимо использовать таблицы сложения и умножения для этой системы.

Чтобы отличить, какая системная система пишется, договоритесь называть ее.

Давайте рассмотрим некоторые из наиболее широко используемых в компьютерах систем счисления.

Бинарный.

В этой системе счисления используются две цифры, 0 и 1. Они представляют число ноль и один разряд соответственно. Основой этой системы счисления является число 2.

Ниже приведены некоторые числа в двоичной записи.

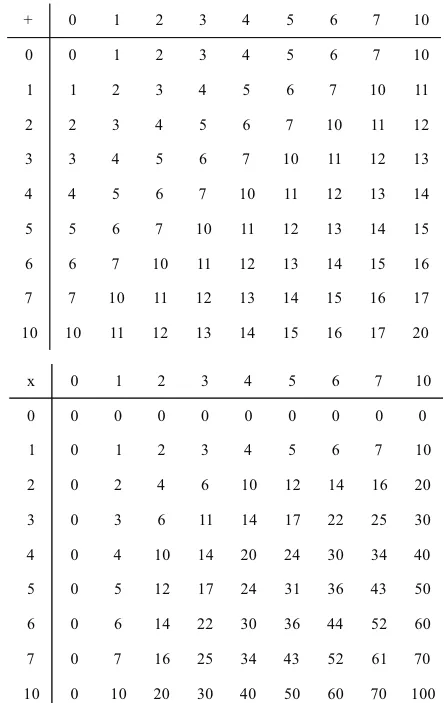
Если вы хотите сложить два числа, записанные в двоичной системе счисления, необходимо использовать дополнительную таблицу.

Таблица умножения в двоичной системе счисления также очень проста.

Единая коллекция цифровых образовательных ресурсов (http://sc.edu.ru/) включает интерактивную анимацию «Преобразование десятичных чисел в цифры» (135050). С его помощью можно наблюдать преобразование любого целого числа в позицию позиционной ноты от 0 до 512, основание которой не превышает 16.

Самая древняя система записи чисел

Жители России не знали чисел, замененных соответствующими символами стоимости. Числа обозначались специальным символом — Titlo — горизонтальной волнистой линией. Например, буква a соответствует 1, b — 2 и d — 3. Десятки имели отдельные буквы: i — 10, k — 20, k — 30 и т.д., а сотни: c f — 200, x — 600.

Египтяне использовали отдельные символы для обозначения чисел. Вертикальные линии использовались для единиц, аналогично букве «l» для десятков, заглавной «e» для сотен и т.д. Например, 345 записывается следующим образом.

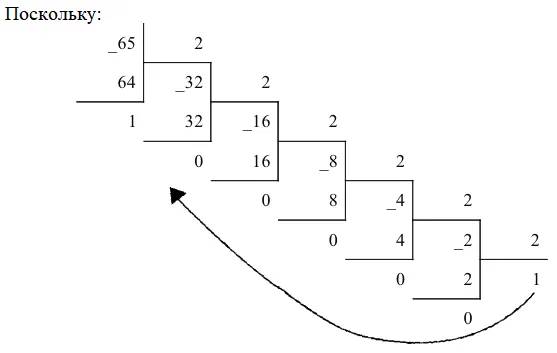
Вавилоняне использовали число 60 SS в своей основе. Благодаря этому наше время составляет 60 минут, а минута — 60 секунд. Для этой СС был характерен сложный метод числовой символики.

Вавилонская и древнерусская системы считаются самыми древними из известных систем счисления.

Были разработаны новые СС для выполнения расчетов с помощью электронных средств. Они сложны и непонятны для людей, но эффективны для машин.

Определение и виды систем счисления

• Возможность записать все числа в нужном диапазоне.
• Естественность представления – любой из комбинаций соответствует только одно значение.
• Обеспечение простоты восприятия и выполнения операций над числами.
• Возможность точного (без или с минимальными погрешностями) перевода значений в другие СС.

Существует два типа арифметических систем: позиционные системы и системы единиц.

Выберите правильный вариант. Буквы, используемые для записи чисел в числовой системе, называются

Позиционная система счисления: что это

Числовая система счисления — это наиболее распространенный тип системы счисления, в которой позиция числа влияет на его значение, но окружающие его значения не влияют на него. Каждая буква обозначает единицу измерения соответствующего числа. Например, помещается десятичное число CC. Если цифра 5 последняя, то она измеряет единицу, вторая обозначает десятки, а четвертая — тысячи. Символы одни и те же, но имеют разное значение.

Преимущества позиционных заметок:.

• Простота запоминания и изображения чисел.
• Удобство совершения математических и логических операций.
• Миниатюрная запись огромных значений.

Числа в информатике включают двоичные, шестнадцатеричные, квадратные и десятичные. Основной системой ЧПУ, используемой в информатике, является двоичная. Это:.

• Обладает минимальными таблицами умножения, сложения.
• Представит любое число посредством двух состояний: единица и ноль.
• Помехоустойчивая по причине всего пары состояний.
• Проста в выполнении арифметических операций.

Шестнадцатеричное число SS также используется в цифровой технике. Его алфавит состоит из первых шести букв латинского алфавита и от D до D.

В десятичной системе используются арабские цифры. Арабские цифры, вероятно, возникли в Индии. Индийская система счисления была описана Аль Кваризми в его работе «Счета Индии».

Десятичная система

Десятичная система счисления, к которой мы привыкли в повседневной жизни, является примером позиционной нотации, с которой мы знакомы с детства и с помощью которой мы производим все наши вычисления. Алфавит десятичной системы состоит из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Алгоритмические числа формируются следующим образом. Значения цифр умножаются на «весовые коэффициенты». Каждое число и все полученные значения суммируются. Это хорошо видно на примере российских цифр.

Основой позиционной символики может быть любое натуральное число q> 1. Наименьшее число всегда равно 0.

Основными преимуществами положительной произвольной системы являются простота числовых манипуляций и ограниченное количество букв, необходимых для представления любого заданного числа.

Позиционная система нумерации, основанная на Q, позволяет представить каждое число в виде

• А — число;
• q — основание системы счисления;
• а_I. — цифры, принадлежащие алфавиту данной системы счисления;
• n — количество целых разрядов числа;
• m — количество дробных разрядов числа;
• q i — «вес» i-го разряда.

Запись числовых значений с использованием уравнения (1) называется расширенным форматом записи. Расширенная форма записи числа выражается в виде 1±a_n-1a_n-2… a₁a₀-1_{… a}… a_{… 1С этого момента рассматриваются только положительные целые числа.} Пример 3.Рассмотрим десятичное число 14351.1. Его сжатая форма настолько хорошо известна, что мы не понимаем, как можно перейти к его развернутой форме, умножая числа на их числовые веса и складывая произведение.

Двоичная система счисления — это позиционная система счисления, основанная на 2. В двоичной системе счисления используются только два числа — 0 и 1.

1.1.2. Двоичная система счисления

Исходя из формулы двоичного целого числа (1), мы можем записать

Эта форма символа «показывает» правила преобразования натуральных двоичных чисел в десятичные символы: в форме двоичных символов необходимо вычислить сумму силы двух, соответствующих единицам.

Из уравнения (1′) выполните правила преобразования целых чисел в двоичные.

Отдельно

n-1_n-1n-2_n-2 —20×2, где коэффициент равен a₀n-1_n-1 —20×2, где коэффициент равен a₁.₀.

.₁.

Это часть двоичного представления исходного числа и совпадает с остатком от последовательного деления на 2.

Поэтому для перевода десятичного целого числа в двоичную систему счисления необходимо указанное число и полученное целое число последовательно разделить на два до получения части, равной нулю. Первое число в двоичной записи синтезируется путем последовательной записи результирующих сегментов, начиная с конца.

Пример 4.Преобразование унарного числа 11 в двоичное. Приведенная выше последовательность функций (алгоритм преобразования) может быть представлена следующим образом

Записывая остаток от деления в направлении, указанном стрелкой, имеем: 11

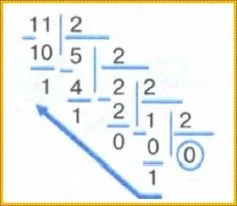
= 1011₁₀.₂.

Восьмеричная система счисления — это позиционная система счисления, основанная на 8. В восьмеричной нотации она используется для записи чисел 0, 1, 2, 3, 4, 5, 6 и 7.

1.1.3. Восьмеричная система счисления

На основании формулы восьмеричного целого числа (1), ее можно записать следующим образом

Пример: 1063

= 1-8 3 + 0-8 2 + 6-8 1 + 3-8 0 = 563₈.₁₀Поэтому, чтобы перевести целое восьмеричное число в десятичную систему счисления, перейдите к его расширенной нотации и вычислите значение полученного выражения.

Чтобы перевести целое число в восьмеричную нотацию, целое число должно делиться на целое число до 8, пока целое число не станет нулем. Первое число в новой нотации заполняется путем последовательной записи результирующих остатков, начиная с конца.

Пример 6.Переведите унарное число 103 в восьмеричную систему счисления.

Система обозначений — это способ представления чисел и соответствующих правил арифметики в терминах чисел. Нотация — это система обозначений, в которой числа записываются по определенным правилам с помощью букв алфавита, называемых цифрами.

Методы нотации можно разделить на три типа: позиционные системы, непозиционные системы и смешанные системы.

Классификация

Изобретение этого типа нумерации приписывается древним шумерам. Здесь значение числа зависит от позиции, занимаемой этим числом. Возьмем для примера 19. Переставьте числа и получите 90.

Позиционные

Системы позиционирования и их использование в математике и информатике, например:.

Здесь позиция числа не важна; количественный эквивалент числа определяется буквой числа.

1. Десятичная – все вы её прекрасно знаете и изучали с первого класса. В качестве алфавита здесь используются цифры от 0 до 9.
2. Двоичная – счисление введенное в семнадцатом веке великим математиком Вильгельмом Лейбницем. В данный момент нашло широкое применение в персональных компьютерах и цифровой технике. Состоит всего из двух знаков 0 и 1.
3. Третичная – состоит из 0, 1 и 2 либо латинских букв A, B, C. На данный момент нигде не применяется. Однако в 1959 году Московским университетом на её основе был выпущен малый компьютер “Сетунь”.
4. Восьмеричная – счисление, широко применяющееся в высокоуровневых языках программирования (например, Java и Python) и разработке цифровой аппаратуры. Свою популярность заслужила из-за легкого перевода в цифровой (двоичный) код. Состоит из цифр от 0 до 7.
5. Двенадцатеричная – распространена на территории Индии и Тибета. Счисление построено на пальце-фаланговом методе счета, при котором большим пальцем считают фаланги той же руки. Попробуйте сами посчитать фаланги, и вы убедитесь, что их действительно 12. Постепенно полностью заменяется десятичной.
6. Шестнадцатеричная – счисление используется в низкоуровневых языках программирования (язык Assembler’а) в информатике. Также в 16-ом виде представляются символы в стандарте Юникода. В её алфавит входят числа от 0 до 9 и латинские буквы A, B, C, D, E и F.

Непозиционные

Пример системы нумерации без позиционирования

Описав классификацию, мы можем теперь говорить о таких понятиях, как база.

– состоит из одного символа. В пример можно привезти зарубки на дереве. Также, скорее всего, каждый из вас видел, как в фильмах люди заключенные в тюрьме считают дни своего заключения, рисуя палочки на стене. Всё это примеры унарного исчисления.
1. Римская – состоит из латинских букв I,X,L,D и M. Нумерация построена с помощью сложения и вычитания. Здесь договорились, что для сложения после большей цифры надо ставить меньшую, а для того чтобы отнять, меньшую цифру ставят перед большей. Например, XI – 11, а IX – 9. – непозиционная нумерация, где цифры представлялись иероглифами.

Смешанные

Этот материал в школьную программу не входит и его достаточно сложно объяснить школьникам, но я все-таки попробую. В смешанной системе исчисления числа с основанием P можно представить числами с основанием Q. Также здесь должно выполняться неравенство Q

Что такое основание

Основание — это числовая цифра, используемая для представления буквы определенной системы счисления.

В математике и информатике он записывается следующим образом.

’20 основано на 10′, что означает, что в определенном алфавите есть 10 букв, которые записывают 10 символов. Это определение используется только в системах позиционной нотации. Символизм низких индексов удобно использовать при работе с различными типами чисел.

Дробные части преобразуются так же, как и целые числа. Однако дробная часть разбивается на группы из трех и четырех цифр справа от десятичной точки, а недостающие цифры дополняются нулями справа.

Рассматриваемые числовые значения относятся к категории позиционной системы. Каждое из этих чисел имеет числовое значение в соответствии с положением числа. Например, в десятичной системе счисления 126 число 100 означает 100, а в числе 216 одно уже другого и означает 10.

Позиционные системы счисления

Каждое число в позиционной нотации может отображаться в усеченной и развернутой формах, например 126: 1*10 2 + 2*10 1 + 6*10 0, то есть 100 + 20 + 6 = 126.

Аналогично, двоичное число 111001 = 1*2 5 + 1*2 4 + 1*2 3 + 0*2 + 0*2 1 + 1*2 0

Восьмеричное число: 247 = 2*8 2 + 4*8 1 + 7*8 0

Шестое число: 2A5F = 2*16 3 + A*16 2 + 5*16 1 + f*16 0

Используя экстенсивную форму, вы можете переводить числа из любой системы счисления в десятичную систему.

Помимо позиционных систем существуют непозиционные системы, в которых положение цифры в числе не влияет на его числовое значение. Например, латинская система счисления основана на i, v, x, l, c, d и m, обозначающих 1, 5, 10, 50, 100, 500 и 1000 соответственно. Таким образом, Рим XVII означает 17, благодаря сложению 10 + 5 + 1 + 1.

Непозиционные системы счисления

Другой пример: число 14 записывается римскими цифрами как XIV. Здесь мы имеем символы x, i и V, означающие 10, 1 и 5. Правило. В соответствии с этим, наименьшее число слева от наибольшего должно быть удалено. То есть i(1) меньше V(5), поэтому 5 — 1 = 4. Тогда число XIV равно 10 + (5-1) = 14.

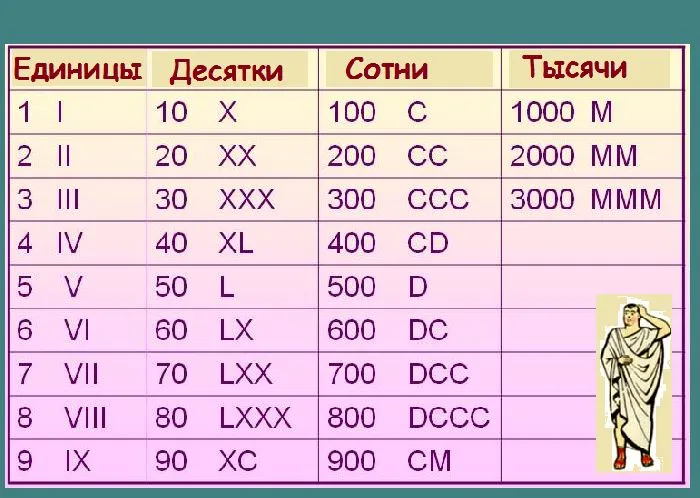
Например, в 1985 году римская система выглядит так: 1000 + (1000-100) + 50 + 10 + 10 + 10 + 10 + 10 + 5 = 1985 год.

Рисунок 2.Таблица с латинскими числами и их значениями.

Первой системой счисления в истории человечества была система единиц, в которой использовался только один символ, а точнее камень, палка или знак. Конечно, в такой системе практически невозможно написать много. Поэтому древние стали заменять группы палочек различными символами.

Рисунок 3.Система нумерации единиц измерения.

Математическая система нумерации