Практические упражнения, как правило, используются на протяжении всего курса, включая начальное закрепление. Они вовлекают учащихся в самостоятельную познавательную деятельность и помогают решить проблему компетентностного подхода к обучению.
Расстояние от точки до прямой — формулы и способы определения
Вычисление расстояния точки от прямой — одна из самых распространенных задач по геометрии в средней школе. Универсальные формулы известны своими решениями, но их использование требует умения применять операции к векторам. Методы, разработанные для определения расстояний между геометрическими элементами, применимы к случаям на плоскости и в трехмерном пространстве.

Точка и прямая
Прежде чем говорить о том, как найти расстояние от прямой линии до точки, необходимо подробно рассмотреть элементы, о которых идет речь.
Известно, что в двух- или трехмерных пространствах геометрии для определения положения объектов вводятся специальные системы координат. Полезно использовать декартову прямоугольную систему, которая представляет пересекающиеся оси под прямыми углами (2 для плоскостей и 3 для трехмерных пространств). Каждый из них имеет масштаб выбранных единиц.
Они обычно однородны. Это означает, что на каждой оси единицей является отрезок одинаковой длины.
Точечный объект
Или просто очки. Это нульмерный объект, который в двумерном пространстве представляет собой набор из двух координат, а в трехмерном пространстве — набор из трех координат. Математически точка описывается как A(x1; y1), где x1 — координаты на оси x, а y1 — координаты на оси y. Чтобы определить значения координат, из точек на соответствующих осях проводят вертикальные линии, пересечения которых указывают на искомые значения. Примеры различных точек на плоскости и в пространстве:.

Точка P находится на оси x, а M — в начальной точке системы координат. В отличие от Q и N, которые могут быть отображены в пространстве, оба отображаются на плоскости. Точки могут иметь и отрицательные координаты, так как координатные оси имеют положительные и отрицательные направления.
Уравнения линии
Прямые линии — один из самых распространенных объектов в геометрии. Они используются для создания многих симметричных форм, таких как пирамиды, призмы, треугольники и прямоугольники (не сферы). Прямая линия представляет собой бесконечный объект в одном направлении и нулевое измерение в двух других направлениях, если говорить о трехмерном пространстве.
Для того чтобы выполнять математические операции над геометрическими элементами, существует несколько типов уравнений, которые их определяют. К ним относятся:.
Первые два типа наиболее часто используются в проблемах. Универсальным уравнением, которое можно легко преобразовать в другие формы, является векторное уравнение. Для трехмерного случая он определяется следующим образом.
(x- y- z)= (x0- y0- z0)+α*(vx- vy- vz).

Где (x; y; z) — координаты любой точки, принадлежащей данной прямой, (x0; y0; z0) — известные точки на объекте, а v (vx; vy; vz) — вектор, параллельный ей. Линия проходит через и называется направляющей. a — произвольный числовой параметр, который может иметь положительные или отрицательные значения. Очевидно, что для квартир количество координат для каждого элемента равно 2.
Векторные уравнения удобны в использовании, так как их легко преобразовать в параметрические или частичные преобразования. В первом случае существует следующая система
Для уравнений в сегментах получаются следующие уравнения
Чтобы получить уравнение общего случая для случая на плоскости из векторной формы, уравнение записывается в виде отрезков, из которых x используется для представления y. Результат будет иметь следующий вид.
Способы определения расстояния
Первое, что необходимо понять, это так называемое расстояние между точкой и линией. Предположим, что существует прямая α и точка A. Если провести отрезок от нулевого объекта на прямой до пересечения с ним под прямым углом в точке A1, то AA1 называется перпендикуляром к a. По определению, расстояние точки от прямой равно длине вертикального отрезка, падающего с нулевого объекта на одномерный объект.

Из геометрической концепции ясно, что длина AA1 является наименьшей из всех возможных отрезков, которые могут быть построены от A до a.
Применение векторных выражений
Как только представление расстояний между геометрическими объектами приобретает смысл, можно переходить к первому универсальному способу решения этой задачи.
Предположим, что существует линия, заданная в векторной форме в двумерном пространстве: (x; y) = (x0; y0) + α∗ (vx; vy).
В той же системе координат дана точка P (x1; y1). Сначала нужно найти вектор u(ux; uy), перпендикулярный направляющей v(vx; vy). Это легко сделать, если помнить, что скалярное произведение вертикальных векторов равно нулю. В результате получается следующее уравнение.
Подстановка любого значения uy в это уравнение дает координаты ux. Если одна из координат вектора v равна нулю, например, vx = 0, uy = 0 для ненулевых значений ux.
Поэтому, когда известны координаты вертикальной направляющей вектора u, можно построить векторное уравнение линии через P.
Далее нам нужно найти точку пересечения двух линий. Для этого представьте y через x в каждой строке и решите систему двух линейных уравнений. Например, возьмем точку Q(x2; y2).
Остался последний шаг для решения этой проблемы. Найдите длину отрезка между точками P и Q. Требуемое уравнение выглядит следующим образом.
Метод, описанный для определения расстояния от прямой линии до точки, может быть использован для решения задач с уровнем. Важно отметить, что в трех измерениях необходимо ввести другое условие для поиска вертикальных сегментов, так как в трех измерениях существует бесконечное количество вертикальных линий в конкретной линии. Заданная прямая и заданная точка. Это усложняет решение проблемы.
Использование формулы
Самый простой способ решения геометрических задач — применение известных формул. Предположим, у нас есть линия, заданная в векторной форме следующим образом.
(x- y- z)= (x0- y0- z0)+α*(vx- vy- vz).

Точка P (x1; y1; z1) также известна. Далее выберите любую точку на прямой и пусть Q (x2; y2; z2). Обратите внимание, что координаты Q удовлетворяют векторному уравнению этой линии. Далее необходимо создать вектор PQ. Его координаты определяются следующим образом.
Векторные уравнения удобны в использовании, так как их легко преобразовать в параметрические или частичные преобразования. В первом случае существует следующая система
Что называется расстоянием от точки до прямой?
Расстояние точки от прямой равно длине перпендикуляра, проведенного из этой точки к прямой. Перпендикуляр — это кратчайшее расстояние от точки до прямой.
Доказательство очень простое. Из точки M на прямой f проведите вертикаль MN и любую прямую MP. Это также известно как градиент. так как градиент всегда больше перпендикуляра.
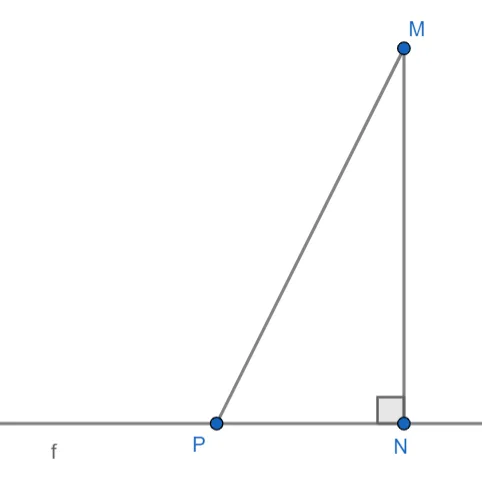
Расстояние между точкой M и прямой f на плоскости задается величиной
Расстояние между параллельными прямыми
А если нужно вычислить расстояние между двумя параллельными путями, какое математическое понятие пригодится в этом случае? Конечно, мы уже догадались, что это расстояние между параллельными прямыми.
Расстояние между параллельными прямыми — это расстояние от одной прямой до другой на плоскости.
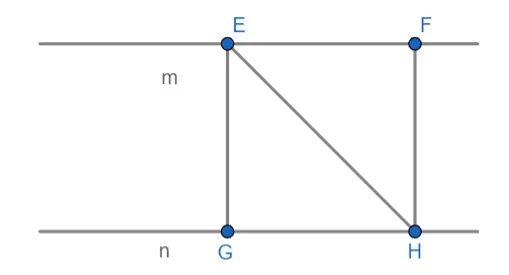
Проверим справедливость этого утверждения, рассмотрев параллельные прямые m и n. Для прямой m выберите две точки E и F, проведите из них перпендикуляр с помощью прямой n, укажите точки пересечения перпендикуляра и прямой n с помощью G и H и соедините E и H отрезком прямой. .
Рассмотрим треугольники GEH и EFH. Сторона EH является общей (как поперечный угол). Таким образом, он является гипотетическим и острым. А из свойств равных треугольников следует, что соответствующие элементы также равны. EG=FH.
Мы пришли к выводу, что расстояние между параллельными прямыми равно длине их общего перпендикуляра.
Расстояние между двумя линиями m и n определяется.
Решение задач
Применяйте свои знания, решая различные задачи.
Задача 1
Точки K, M и N отмечены на клетчатой бумаге размером с клетку. Каково расстояние от прямой MN до точки K?
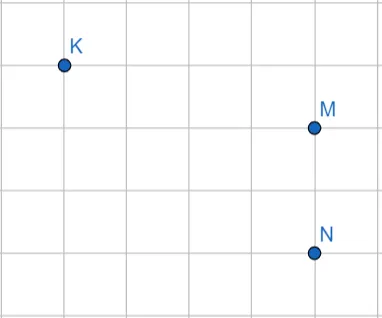
Как вы помните, чтобы найти расстояние от прямой до точки, нужно провести вертикальную линию от точки до прямой и вычислить ее длину.
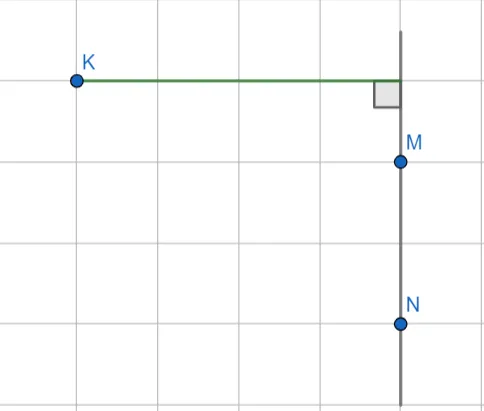
Ответ: 4 см.
Задача 2
Используя данные чертежа, найдите расстояние от Q до прямой PR.
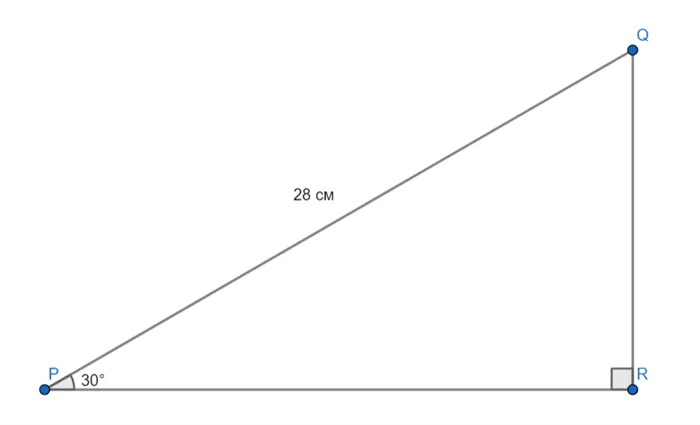
На чертеже видно, что QR перпендикулярен PR, поэтому QR — это расстояние от Q до PR. Поскольку QR перпендикулярна линии PR, QR составляет половину диагонали, то есть 14 см.
Ответ: 14 см.
Задача 3
QS — биссектриса равностороннего треугольника PQR, а ST — расстояние S от прямой QR, равное 12 см. Каково расстояние от линии PR до Q?
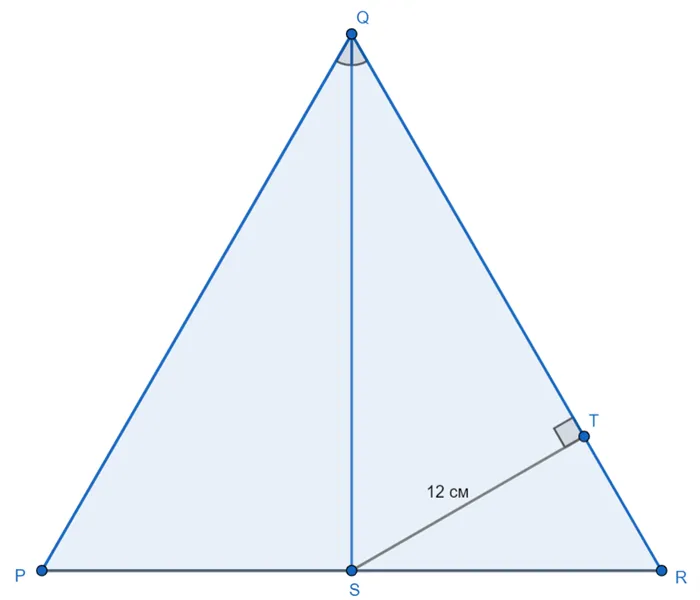
Это равносторонний треугольник, так как по условию QS — биссектриса.
ST — это расстояние от S до линии QR, и поэтому предполагается, что они ортогональны. Кроме того, QS = 2ST = 24 см, так как ST — это ножка угла по отношению к.
Поскольку это равносторонний треугольник, QS не только рассечен, но и приподнят.
Ответ: 24 см.
А что если линия в плоскости слишком далека, чтобы провести перпендикулярную линию, что, конечно, имеет место? В этом может помочь вид расстояния в координатах от точки до линии.
Если уравнение задано прямой f: ax + by + c = 0 и имеется точка M с координатами, то уравнение расстояния от точки до прямой на плоскости имеет вид
Задача 4
Найдите расстояние от точки M (36; 6) до прямой f: 6x + 2y-12 = 0.
Нет необходимости рисовать линии или точки. Нет необходимости выбирать масштаб, соответствующий перпендикуляру. Просто используйте следующую формулу.
Конечно, можно вычислять и без координат, но приведенный выше вариант является наиболее разумным и удобным.
На занятиях по математике в онлайн-школе Skysmart вы всегда узнаете различные способы экономии времени на контрольных и экзаменах. Выберите курс, который соответствует вашему уровню и целям обучения, и начинайте получать удовольствие!
При такой форме символики нетрудно определить, что нормальный вектор этой линии имеет координаты (3; -1). Этот же вектор является направляющим вертикальным вектором.
Расстояние от точки до прямой. Расстояние между параллельными прямыми

После уточнения так называемого расстояния между двумя точками сначала вводится понятие расстояния от точки до прямой, а затем понятие расстояния между параллельными прямыми.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам из комплекта, необходимо приобрести его в каталоге и добавить в личный кабинет.



Конспект урока «Расстояние от точки до прямой. Расстояние между параллельными прямыми»
Расстояние между двумя точками A и B равно длине отрезка AB, соединяющего эти точки.
Обратите внимание, что точки A и B также могут быть объединены таким образом.
Однако кратчайший маршрут, или отрезок AB, — это расстояние между этими точками.
Возьмем некоторую прямую b и точку A, которая не лежит на этой прямой. Пусть A — перпендикуляр, проведенный из A к прямой b.
Полученный отрезок NA называется расстоянием от A до прямой. Потому что это минимальное расстояние между данной точкой и линией.
Действительно, это так. Отметьте точку B на прямой b и рассмотрите прямоугольный треугольник AHB.
AB — гипотенуза, а AH — наклонная плоскость треугольника. Известно, что катет всегда меньше гипотенузы.
AB называется градиентом от точки A к линии b.
Перпендикуляр, проведенный из точки к прямой линии, меньше любого градиента, проведенного из той же точки к прямой линии.
Длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от точки до прямой.
Он символизируется следующим образом:.
Пусть a и b — параллельные прямые. Отметьте две точки A и B на прямой a и проведите из них перпендикуляры AM и BN на прямой b.
b для прямой a|| и отрезков AM⊥b и BN⊥b, где AM = BN и равно расстоянию между параллельными прямыми a и b.
Начертите отрезок AN и рассмотрите треугольники ABN и AMN.

После AM⊥b, и a || b, тогда AM⊥a. отсюда BN⊥b, и a || b, тогда BN⊥a.
Мы видим, что ABN и AMN — правильные треугольники. Их стороны IF являются общими и представляют собой гипотенузы обоих треугольников. Углы ABN и ANM равны, потому что они внутренне склеены с параллелями AB и MN и с квадратиком AN.
Поэтому прямые треугольники ABN и AMN равны косому и острому углам. AM=BN.
Видно, что отрезки AM и BN равны.
Расстояние между двумя прямыми линиями равно длине их общего перпендикуляра.
Он символизируется следующим образом:.
Обратное утверждение также применимо.
Все точки плоскости, находящиеся по одну сторону от прямой и равноудаленные от нее, лежат на прямой, параллельной ей.

На этой диаграмме отрезок AB = 6 см, а ∠Β = 30 градусов. Найдите расстояние от прямой a до точки A.
Расстояние от точки A до прямой α — перпендикуляр AC.
Получен прямоугольный треугольник ABC. ∠ Угол B = 30 градусов, а AB = 6 см.
Известно, что катет прямоугольного треугольника под углом 30 градусов равен половине наклонной стороны. Мы получаем:.
На этой диаграмме расстояние между параллельными прямыми α и β равно 5 см, а расстояние между параллельными прямыми α и γ равно 9 см. Каково расстояние между параллельными прямыми b и c?
Составьте математическую модель реальной ситуации в своем блокноте. Проведите произвольную прямую a и отметьте точку A, которая не лежит на прямой. Проведите перпендикулярную линию от A до a (сколько их можно провести?). -Один ученик на доске.
Решение задачи
Чтобы интегрировать материалы, решите следующую короткую задачу Пусть 3 — точка на плоскости: a (1; 0), b (2; -3), c (-1; 1), то есть треугольник с вершинами и сторонами ab, bc и ca. Нам нужно найти расстояние от точки c до линии av.

Сначала нужно найти вектор направления линии. Его координаты соответствуют следующим значениям
Далее необходимо найти вектор переменного тока.
Вы можете предварительно вычислить коэффициенты векторного произведения AB*AC и длину AB перед нахождением расстояния по формуле
Расстояние d от точки C до прямой, проходящей через точки A и B, равно.
d = 5/10 0, 5 ≈ 1,58 единиц длины.
Поэтому существует два способа определения расстояния между известной линией и точкой в пространстве.

Первый требует использования ряда математических вычетов при расчете. Это относится только к проблемам уровня. Второй метод позволяет использовать универсальные типы.
Точки O и F — середины ребер BC и AB тетраэдра DABC, соответственно. Докажите, что DO = CF (рис. 127, a и b).
Определение расстояние от точки до прямой в пространстве
Вычислите расстояние между точкой и прямой в пространстве, используя уравнение

где ˉ(x_0, y_0, z_0 \) — координаты конкретной точки- (x_1, y_1, z_1 \) — координаты нормального вектора конкретной линии- ˉ(l, m_1, n_1 \) — координаты водителя векторной линии.
Эта формула похожа на формулу уровня, но кажется более сложной. Если вы знаете принципы решения уравнения массива, то в вычислениях нет ничего сложного.
Вам трудно понять это самостоятельно?
Обратитесь за помощью к своему учителю.
Посмотрите, как можно использовать эту формулу для решения задач.
Например, линия m задается \1}<(x-5)\over1>=<(y+1)\over2>=<(z-4)\over4>\ʔ), координаты точки ʔ (K \) (1; 2; 3).
Требуется определить расстояние в пространстве между точкой ⌘(K \) и прямой ⌘(m \).
Направляющий вектор линии m имеет координаты (1; 2; 4), а вектор нормали равен (-5; -1; 4).
Подставляя все значения в формулу, получаем
Ответ: расстояние в пространстве между точкой ⌘ (K \) и прямой ⌘ (m \) равно 5 080.
Не нашли нужную информацию?
Закажите соответствующий материал в нашей службе. У вас есть 59 секунд, чтобы отправить свою работу, и она будет автоматически отправлена в течение 59 секунд. Правильный выбор специалиста позволит вам сэкономить время и силы на учебе.
Вся работа выполняется без посредников, поэтому цена вас приятно удивит.
Улучшения и советы включены
Часть работы выполняется бесплатно и в оговоренные сроки.
Если работа не будет выполнена, мы вернем вам деньги.
Если специалист не справится с этой задачей, мы гарантируем 100% возврат денег.
Техническая поддержка доступна 24 часа в сутки 7 дней в неделю.
Наши менеджеры работают без выходных и праздников, чтобы оперативно ответить на ваши вопросы.
Тысячи сертифицированных экспертов.
Мы выбираем только надежных исполнителей — экспертов в своей области. Все они имеют высшее образование на «хорошо» и «отлично».

Гарантия возврата денег
Эксперты получили деньги, но не выполнили работу? Не с нами!
В течение срока действия задания и гарантии деньги хранятся на вашем балансе.
Если возникнут проблемы, мы гарантируем полный возврат денег.