Произведение чисел это что. Произведение чисел это что

Содержание

Рассмотрим пример: Чтобы нам не писать длинную запись можно записать ее в виде умножения. Число 2 повторяется 11 раз поэтому пример с умножением будет выглядеть так: 2⋅11=22

Умножение и деление целых чисел

При умножении и делении целых чисел действуют другие правила. В этом уроке мы рассмотрим каждый из них.

При умножении и делении целых чисел обращайте внимание на знак чисел. Это определяет правила, которые применяются. Вам также нужно будет выучить некоторые правила умножения и деления. Изучение этих правил поможет вам избежать досадных ошибок в будущем.

Законы умножения

Некоторые из законов математики мы рассматривали в «Законах математики». Однако мы не изучили все законы. Существует множество законов математики, и разумно изучать их в том порядке, в котором они необходимы.

Во-первых, давайте вспомним, что такое умножение. Умножение состоит из трех параметров: коэффициента, множителя и произведения. Например, в уравнении 3 x 2 = 6 число 3 является коэффициентом, число 2 — множителем, а число 6 — произведением.

Множитель указывает, что именно умножается. В данном примере умножается число 3.

Множитель указывает на то, во сколько раз нужно увеличить множитель. В данном примере множителем является число 2. Множитель указывает на то, во сколько раз нужно увеличить множитель 3. Таким образом, операция умножения умножает число 3 на коэффициент 2.

На самом деле произведение — это результат действия умножения. В данном примере продуктом является число 6. Произведение является результатом умножения 3 на 2.

Выражение 3 x 2 можно также понимать как сумму двух троиц. Множитель 2 указывает, сколько раз нужно повторить число 3.

Так, если число 3 повторяется два раза подряд, то в результате получается число 6.

Переместительный закон умножения

Умножения и перемножения обозначаются общим словом multiplier. Транспозиционный закон умножения работает следующим образом.

Изменение положения фактора не изменяет продукт.

Давайте проверим, так ли это. Умножьте 3 на 5. Здесь 3 и 5 являются множителями.

Затем поменяйте местами факторы.

В обоих случаях мы получим ответ 15, поэтому между выражениями 3 x 5 и 5 x 3 можно поставить знак равенства, так как они равны одному и тому же значению.

Тогда, используя переменные, закон умножения можно записать как

Сочетательный закон умножения

Этот закон гласит, что если выражение состоит из нескольких элементов, то продукт не зависит от последовательности действий.

Например, формула 3 x 2 x 4 состоит из многих элементов. Чтобы вычислить его, умножьте 3 на 2, а затем умножьте полученное произведение на остаток 4. Получено следующее.

3 x 2 x 4 = (3 x 2) x 4 = 6 x 4 = 24

Это было первое решение. Второй вариант — умножить 2 на 4, а затем умножить полученное произведение на остаток числа 3. Это дает следующее.

3 x 2 x 4 = 3 x (2 x 4) = 3 x 8 = 24

В обоих случаях ответ — 24. Поэтому, поскольку выражения (3 x 2) x 4 и 3 x (2 x 4) имеют одинаковое значение, между этими выражениями можно поставить знак равенства.

Используя переменные, комбинаторный закон умножения можно записать как

a x b x c = (a x b) x c = a x (b x c)

где a, b и c могут быть любыми числами.

Распределительный закон умножения

Закон распределения позволяет умножить сумму на число. Для этого умножьте каждый сумматор суммы на его числовое значение, а затем сложите результат.

Например, найдите значение выражения (2 + 3) x 5

Выражение в скобках — это сумма. Умножьте эту сумму на число 5. Для этого умножьте каждый член суммы, то есть числа 2 и 3, на число 5, а затем сложите результат.

Умножение целых чисел

Пример 1. Найдите значение выражения — 5 x 2

Это умножение чисел на различные знаки. -5 — отрицательное число, а 2 — положительное. В этих случаях необходимо применять следующие правила

Чтобы умножить число на разные знаки, умножьте числитель и поставьте знак минус перед ответом.

-5 x 2 = — (| -5 | x | 2 |) = — (5 x 2) = (10) = -10

Обычно записывается в краткой форме: -5 × 2 = -10

Каждое умножение может быть выражено в виде суммы чисел. Например, рассмотрим выражение 2 × 3.

Множителем этого выражения является число 3. Этот множитель показывает число, умноженное на два. Однако 2×3 можно понимать как сумму трех дуалов.

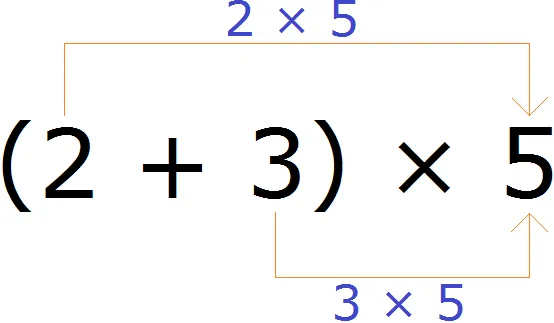
То же самое происходит и с уравнением — 5 x 2. Это выражение можно представить как сумму

и выражение (-5) + (-5) равно -10. Мы знаем это из предыдущего урока. Это дополнения с отрицательным числом. Вспомните, что результатом сложения отрицательных чисел является отрицательное число.

Пример 2. Найдите значение уравнения 12 x (-5).

Это умножение чисел с разными знаками. 12 — положительное число, а (-5) — отрицательное. Снова примените предыдущее правило. Перемножьте произведения чисел и поставьте минус перед полученным ответом.

12 x (-5) = — (| 12 | x | -5 |) = — (12 x 5) = — (60) = -60

Решения обычно пишутся короткими предложениями.

Пример 3. Найдите значение 10 x (-4) x 2

Существует несколько факторов, которые способствуют такому выражению. Сначала умножьте 10 на (-4), а затем умножьте это значение на 2. В то же время применяйте правила, которые вы выучили ранее.

Первое действие:.

10 x (-4) = — (| 10 | x | -4 |) = (10 x 4) = (-40)

Второе действие:.

-40 x 2 = — (| -40 | x| 2 |) = — (40 x 2) = — (80) = -80

Поэтому значение 10 x (-4) x 2 равно -80.

Пример 4. Нахождение значения выражения (-4) × (-2)

Это умножение отрицательных чисел. В этих случаях необходимо применять следующие правила

Чтобы умножить отрицательное число, умножьте на модуль и поставьте его перед ответом; вы получите Syn.

Поскольку мы традиционно не пишем плюс, мы просто пишем ответ 8.

Запишите решение (-4) x (-2) = 8

Возникает вопрос, почему при умножении отрицательного числа вдруг получается положительное число. （Докажем, что (-4) × (-2) равно 8.

Сначала напишите следующее уравнение.

Добавьте к этому уравнению уравнение (-4) × (-2). Мы также поместили их в скобку:.

Мы все приравниваем их к нулю.

Теперь наступает самое интересное. Дело в том, что нам нужно вычислить левую часть этого уравнения и в итоге получить ноль.

Таким образом, первое произведение (4x(-2)) равно -8. Напишите -8 в формуле вместо произведения (4x(-2)).

Временно замените второй продукт на тире

Тогда выражение -8 + … = 0. Ответ очевиден: второй продукт — это тире. Недостаток должен быть заменен положительной 8 и другим числом. Это единственный способ сохранить равенство. -8 + 8 равно 0, потому что.

Рассмотрим пример: Чтобы нам не писать длинную запись можно записать ее в виде умножения. Число 2 повторяется 11 раз поэтому пример с умножением будет выглядеть так: 2⋅11=22

Произведение чисел это что

Важные математические практики являются продуктами чисел. Произведение, умножение и т.д. — что скрывается за этими словами. Именно это и является целью нашей статьи. Давайте начнем с мелочей. Когда происходит много событий, очень трудно сохранить даже информацию. Каким-то образом мы должны уменьшить его до компактного. Допустим, у вас в гардеробе больше двух пар носков. Да, конечно, мы можем написать 2+2+2+2+2 Это неоправданно удобно, пока вы не добавите второе число, связанное с парой носков, т.е. 15, например. Она поставила их в магазин! И здесь проще выразить это в таких терминах У нас есть две пары носков, сфотографированных много раз!

Здесь формируется та самая магия перехода от обычной суммы к произведению, когда подразумевается, что иногда получается число. Пришло время дать определение.

Определение произведения чисел

Произведение двух чисел есть не что иное, как приобретение одним из чисел количества другого числа.

Также! Если продукт равен C, то при количестве не менее b часов получается одно номинальное значение количества, которое и является продуктом. Его можно записать следующим образом

C = A1+A2+A3+A4. +ab, где 1,2,3,4. B — показатель того, что это за число.

Найдите номер примера ‘Product:’.

1) 1.2⋅3;

Ответ: 1,2⋅3= 3,6

2) 4⋅5⋅13

Ответ: 4⋅5⋅13= 260

Свойства произведения чисел

Конфигурация: n⋅m=m⋅nФункция:(n⋅m)⋅k=n⋅(m⋅k)Исходя из этих свойств, можно сделать вывод, что при перестановке множителя значение произведения остается неизменным.

Примеры удобных способов нахождения чисел:.

1) 5⋅17⋅2; 2) 7⋅2⋅15⋅55

Решение. Из свойств умножения:.

5⋅17⋅2= (5 страхов) ⋅17= 10⋅17= 1707⋅2⋅15⋅5= (7⋅15) ⋅5= (7⋅30) ⋅5= 210⋅5 = 1050ответ.

5⋅17⋅2= 1707⋅2⋅15⋅5= 1050

Там, где устное умножение чисел затруднено, используется умножение в столбик. Умножение в столбик можно применять к большим натуральным числам или десятичным дробям.

Примеры чисел ‘найти произведение

1) 156⋅32; 2) 4,71⋅3,1

Разрешение. Запишите числа, которые нужно перемножить, в столбики. Сначала умножьте единицы второго числа на первое число и запишите произведение в строку. Затем умножьте десятки второго числа на первое число. Под первым произведением запишите результат только на одну цифру левее. Наконец, используйте правило сложения столбиком, чтобы найти сумму произведений

Умножение десятичных дробей во втором примере выполняется следующим образом Умножение дробей как целых чисел путем игнорирования сторон и деления на соответствующее количество цифр числа, равного сумме цифр после запятой. Факторные баллы. В нашем случае первый фактор имеет два десятичных знака, а второй — один десятичный знак. Поэтому в ответе необходимо выбрать правильный десятичный знак.

Ответ.

156⋅32= 49924.71⋅3,1= 14,601

Закон распределения позволяет умножить сумму на число. Для этого умножьте каждый сумматор суммы на его числовое значение, а затем сложите результат.

Сочетательный закон умножения.

(2⋅3)⋅4=6⋅4= 24 или 2⋅(3⋅4)=2⋅12= 24 имеем, (2⋅3)⋅4=2⋅(3⋅4)(a⋅b)⋅C=a⋅(bbe c)

Свойство комбинаторного метода умножения: чтобы умножить число на произведение двух чисел, можно сначала умножить первый множитель, а затем умножить полученное произведение на второй множитель.

Различные множители могут быть заключены в скобки взаимозаменяемо, а результат или продукт остается тем же.

Эти законы применимы к каждому натуральному числу.

Умножение любого натурального числа на единицу.

Рассмотрим пример: 7 страх точка = 7 или 1⋅7= 7 a страх 1 = a или 1⋅a= a Если натуральное число умножить на единицу, то произведением всегда будет то же самое число.

6⋅0= 0 или 0⋅6= 0a⋅0= 0 или 0⋅a= 0Если любое натуральное число умножить на ноль, то произведение будет равно нулю.

Вопросы по теме «распространение»:.

Что такое произведение чисел? ОТВЕТ: Умножение числа или чисел представляет собой выражение m⋅n, где m — сумма, а n — количество повторений этой суммы.

Какова цель умножения? Ответ заключается не в том, чтобы написать много чисел, а в том, чтобы написать их вместе. Например, 3+3+3+3+3+3+3+3 =3⋅6= 18

Что является результатом умножения? Ответ: стоимость продукта.

Что подразумевает символика умножения? Ответ: 3⋅5 = 5+5+5 = 3+3+3+3+3+3+3+3+3 = 15

Чему равно произведение при умножении миллиона на ноль? Ответ: ноль.

Пример №1: Замените общее число произведением: а) 12+12+12+12+12+12 б) 3+3+3+3+3+3+3+3+3+3+3+3+3 Ответ: а) 12⋅5= 60 б) 3⋅9= 27

Пример 2: Запишите в виде произведения: a) a+a+a+a+a+a б) c+c+c+c+c+c решение: a) a+a+a+a+a+a =4⋅ab) c+c+c+c+c+c+c =7⋅g

Задача 1: Мать покупает три коробки шоколадных конфет. В каждой коробке находится 8 конфет. Сколько кусочков шоколада купила моя мама? Решение: в коробке восемь конфет, а таких коробок три. 8+8+8+8 =8⋅3= 24 конфеты Ответ.

Задача №2: Учитель рисования велел восьми ученикам подготовить к уроку по семь карандашей. Сколько карандашей было у детей? Решение: можно измерить сумму проблем. У первого ученика было семь карандашей, у второго — семь карандашей и т.д. 7⋅8= 56Ответ: 56 карандашей.

Добавить комментарий Отменить ответ

Вы должны войти в систему, чтобы написать комментарий.

Это нужно для деления отрицательных чисел. Чтобы решить этот пример, разделите коэффициент делимого на коэффициент делителя и поставьте символ плюс перед полученным ответом.

Умножение многозначного числа на однозначное

Умножение 8094 x 3 описывается расстановкой точек под коэффициентами, размещением символа умножения слева и проведением линии, разделяющей произведения.

Чтобы найти сумму трех одинаковых слагаемых, проверьте, что три средства многозначного числа 8094 являются тремя средствами многозначного числа 8094.

Поэтому для умножения многозначного числа все команды умножения должны быть умножены три раза, т.е. три единицы, десятки, сотни и т.д. Поскольку сложение начинается с единицы, умножение должно начинаться с единицы и переходить справа налево к единицам более высокого порядка.

При этом ход расчета представляется устно.

Начните умножение на единицы: 3 x 4 равно 12, 2 под единицей равно 2, а единицы (1 10) применяются к продукту следующего класса путем умножения (или запоминания в уме).

Умножьте на десятки: 3 x 9 получается 27, да, если иметь в виду 28-синус под 8 и 2.

Умножайте на сотни: ноль, умноженный на три, дает ноль, а да 2 — держит в уме 2.

Умножение на тысячи: 3 x 8 = 24, знак 24, так как нет следующего порядка.

Это действие выражается в письменной форме.

Из предыдущего примера вытекают следующие правила Для умножения многозначного числа на однозначное требуется

Подпишите множитель под единицей умножения, поставьте знак умножения слева и проведите черту.

Умножение начинается с простой единицы и перемножает десятки, сотни, тысячи и т.д. с правой руки на левую.

Если при умножении произведение представлено одной цифрой, то она подписывается под числом умножаемого элемента.

Если произведение представлено двузначным числом, то количество единиц подписывается под тем же столбцом, а десятки прибавляются к произведению следующей степени с помощью множителя.

Умножение продолжается до тех пор, пока не появится полный продукт.

Изменение произведения чисел при изменении его сомножителей

Чтобы понять, что происходит с произведением чисел при изменении одного или нескольких факторов, необходимо помнить, что акт умножения — это частный случай акта сложения, комбинация закона изменения и сложения.

Если один из факторов увеличивается во много раз, то и продукт увеличивается во столько же раз.

Рассмотрим пример 18∙2. Например, если мы увеличим второй коэффициент в три раза, то получим другое уравнение: 18∙6.

Умножение любого натурального числа на нуль

6⋅0=0 или 0⋅6=0a⋅0=0 или 0⋅a=0 Умножение любого натурального числа на ноль дает произведение ноль.

Вопросы по теме «распространение»:.

Что такое произведение чисел? ОТВЕТ: Произведением чисел или умножением чисел является выражение m⋅n Где m — сумма, а n — количество повторений этой суммы.

Какова цель умножения? Ответ заключается в том, чтобы не писать длинные сложения чисел, а писать их в сокращенном виде. Например, 3 + 3 + 3 + 3 + 3 + 3 +3=3⋅6=18

Что является результатом умножения? Ответ: стоимость продукта.

Что означает символ умножения 3⋅5? Ответ: 3⋅5 = 5 + 5 + 5 + 5 = 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 15

Если 1 миллион умножить на ноль, что получится? Ответ: ноль.

Пример 1: Замените общее число произведением: a) 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 b) 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 Ответ: a) 12⋅5 = 60 b) 3⋅9 = 27

Пример 2: В виде произведения запишите: а) α+α+α+α+α+α+α б) γ+γ+γ+γ+γ+γ+γ Ответ: а) α+α+α+α+α+α+α= 4⋅α б) γ+γ+γ+γ+γ= 7⋅γ

Вопрос 1: Мать купила три коробки шоколадных конфет. Каждая коробка содержит 8 конфет. Сколько шоколадных конфет купила мать? Решение: в одной коробке 8 конфет, а таких коробок 3. 8 + 8 + 8 = 8⋅3 = 24 конфеты Ответ: 24 конфеты.

Вопрос #2: Учитель рисования сказал восьми ученикам нарисовать по семь карандашей на урок. Сколько карандашей было у детей? Решение: подсчитайте общее количество проблем. У первого ученика было семь карандашей, у второго ученика — семь карандашей. 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 = 56 Символика неприятна и длинна, поэтому замените сумму произведением. 7 ⋅ 8 = 56 Ответ: 56 карандашей.