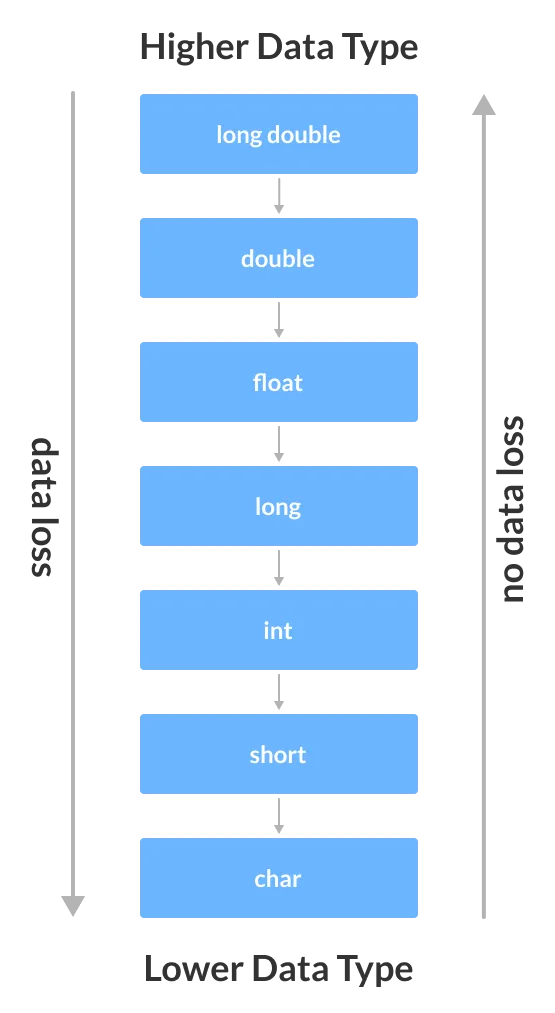
Алгоритм прозрачности всегда должен завершаться за конечное число шагов, но это число не ограничено. Объемные алгоритмы применяются к определенным категориям входных данных (например, числа, пары чисел, наборы букв и т.д.). Не имеет смысла строить алгоритм, который находит наибольший общий делитель одной пары чисел 10 и 15.
Учитель информатики
Информатика. Шаг 8.БосоваЛ.Л. Оглавление.
Ключевые слова.
- алгоритм
- свойства алгоритма
- дискретность
- понятность
- определённость
- результативность
- массовость
- исполнитель
- характеристики исполнителя
- круг решаемых задач
- среда
- режим работы
- система команд
- формальное исполнение алгоритма
2.1.1. Понятие алгоритма
Каждый человек в повседневной жизни, в школе и на работе решает огромное количество задач различной сложности. Сложные задачи требуют длительного обдумывания решения, в то время как простые и привычные задачи решаются автоматически, без раздумий. В большинстве случаев решение каждой задачи можно разбить на простые шаги. Многие такие задачи (например, установка программного обеспечения, сборка шкафчика, создание веб-сайта, управление техническим устройством, покупка билетов на самолет через Интернет) уже разработаны и снабжены пошаговыми инструкциями. В результате они могут привести к желаемым результатам.
Пример 1. Задача «найти среднее арифметическое двух чисел» может быть решена в три этапа
- 1) задумать два числа;
- 2) сложить два задуманных числа;
- 3) полученную сумму разделить на 2.
Пример 2. Задача «положить деньги на телефонный счет» разбита на следующие шаги
- 1) подойти к терминалу по оплате платежей;
- 2) выбрать оператора связи;
- 3) ввести номер телефона;
- 4) проверить правильность введённого номера;
- 5) вставить денежную купюру в купюроприёмник;
- 6) дождаться сообщения о зачислении денег на счёт;
- 7) получить чек.
Пример 3.На схеме показаны шаги по решению задачи «Нарисуй счастливого ежика».

На первый взгляд, нахождение среднего арифметического, внесение денег на телефонный счет и рисование ежика — это совершенно разные процессы. Однако у них есть одна общая черта. Каждая из этих процедур описана в виде серии коротких шагов, которые при правильном выполнении приведут к желаемому результату. Последовательности команд, показанные в примерах 1-3, являются алгоритмами решения соответствующих задач. Исполнителями этих алгоритмов являются люди.
Алгоритм может быть описанием серии вычислений (пример 1) или нематематических шагов (примеры 2-3). В обоих случаях, однако, начальные условия (исходные данные) и то, что произойдет (результаты), должны быть четко определены до начала разработки. Алгоритм — это описание серии шагов для решения проблемы, начиная с исходных данных и заканчивая желаемым результатом.
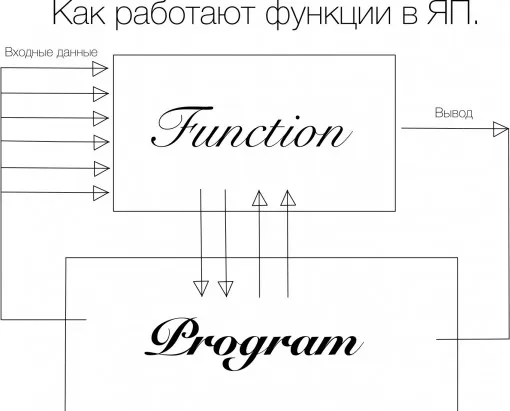
В целом, форма алгоритма может быть представлена следующим образом (рисунок 2.1)
Алгоритмы — это правила сложения, вычитания, умножения и деления чисел, многие грамматические правила и правила геометрического построения, которые мы изучаем в школе.
Анимации «Алгоритмические операции» (193576), «Меньшие общие числа» (170363) и «Меньшие общие числа» (170390) помогают вспомнить некоторые алгоритмы, изучаемые на уроках русского языка и математики. (http:/ /sc.edu.ru/).
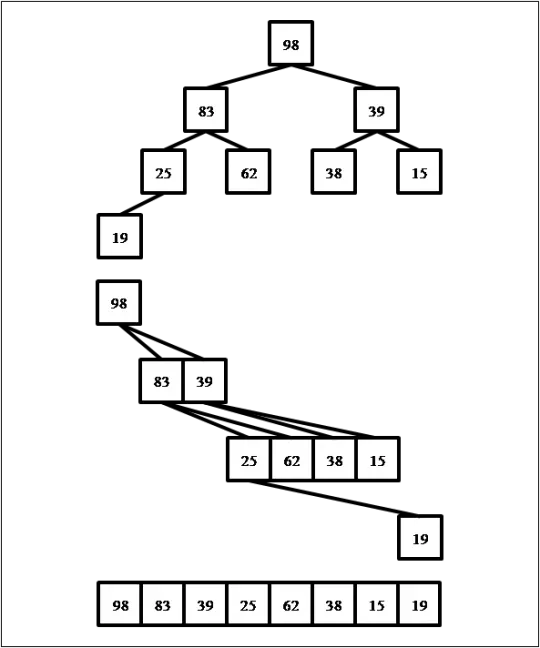
ПРИМЕР 4. Алгоритм генерирует новую строку символов из строки следующим образом.
- 1. Вычисляется длина (в символах) исходной цепочки символов.
- 2. Если длина исходной цепочки нечётна, то к исходной цепочке справа приписывается цифра 1, иначе цепочка не изменяется.
- 3. Символы попарно меняются местами (первый — со вторым, третий — с четвёртым, пятый — с шестым и т. д).
- 4. Справа к полученной цепочке приписывается цифра 2.
2.1.2. Исполнитель алгоритма
Каждый алгоритм предназначен для конкретного исполнителя.
Исполнители — это объекты (люди, животные, технические устройства), которые могут выполнять определенный набор команд.
Различают формальных и неформальных исполнителей. Обычный исполнитель всегда выполняет одни и те же команды одним и тем же способом. Неформальные исполнители могут выполнять команды по-другому.
Давайте подробнее рассмотрим типичный набор исполнителей. Типичные исполнители очень разные, но каждый из них может определить характеристики объема (цели) выполняемого задания, среды, системы управления и режима работы.
Объем выполняемых задач. Каждый исполнитель создан для решения определенного круга задач, таких как создание символов, выполнение расчетов или проектирование уровней.
Интерпретационная среда. Сектор, среда и условия, в которых работает исполнитель, обычно называются окружением исполнителя. Исходные данные и результаты алгоритма всегда принадлежат среде организма, для которого предназначен алгоритм.
Система команд исполнителя. Команды, которые выполняют одно интегрированное действие на исполнителе, называются командами. Набор всех команд, которые могут быть выполнены путем конфигурирования системы команд исполнителя (ACS). Алгоритм формируется путем рассмотрения функции конкретного исполнения, т.е. системы команд исполнителя, которая его выполняет.
Метод работы. Большинство исполнителей оснащены функциями немедленного и программного управления. В первом случае исполнитель ожидает команд от человека и немедленно выполняет все полученные команды. Во втором режиме исполнитель сначала предоставляет полную последовательность команд (программу), а затем выполняет все эти команды в автоматическом режиме. Некоторые исполнители работают только одним из этих способов.
Давайте рассмотрим пример руководителя-исполнителя.
Пример 5. Исполнительная черепаха перемещается по экрану компьютера, оставляя линии в форме линий. Командная система «Черепаха» состоит из двух команд.
- 1) Вперёд n (где n — целое число) — вызывает передвижение Черепашки на n шагов в направлении движения — в том направлении, куда развёрнуты её голова и корпус;
- 2) Направо m (где m — целое число) — вызывает изменение направления движения Черепашки на m градусов по часовой стрелке.
Повторное написание k означает, что последовательность команд в скобках повторяется.
Рассмотрим, какая фигура появится на экране после того, как черепаха выполнит следующий алгоритм.
Повторите 12 правых 45 передних 20 правых 45
Пример 6.Система команд исполнителяИсполнитель состоит из двух команд, соответствующих числам.
Первое число уменьшается на 1, а второе увеличивается в числе на 3. При описании алгоритма указывается только количество команд. Например, алгоритм 21212 означает следующую последовательность команд.
Используя этот алгоритм, число 1 преобразуется в 15: ((1-3-1)-3-1)-3 = 15.
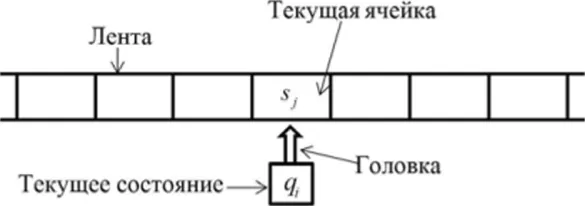
Пример 7.Робот движется по клеточному полю со стенами между соседними клетками. Робот перемещается по квадрату поля и может выполнять следующие команды
Лучшее представление о том, как найти первое число, можно получить в анимации «Сетка Эратосфена» (180279), размещенной на единой коллекции цифровых учебных ресурсов.
Бесконечность не предел
Но прежде чем мы это сделаем, давайте вспомним немного математики. Из школьной математики мы знаем, что существует бесконечное число — независимо от того, насколько оно велико, к нему всегда можно прибавить еще больше, чтобы получить еще больше. Обычно это ограничение в школе. В университете на уроках высшей математики вам расскажут, что на самом деле существуют различные виды бесконечности. Множества, которые могут быть пронумерованы натуральными числами, считаются измеримыми бесконечностями. Эти множества дают сами натуральные числа (число 1 дает число 1, число 2 — число 2 и т.д.). число 1, третье число — 1, т.е. каждое положительное число k получает число 2k, каждое отрицательное число — m получает число 2m + 1). Измеримое бесконечное множество включает числа, представленные в виде шкалы, нежелательные и даже рациональные числа (числа, представленные в виде дробей m/n, где числа не поддаются регистрации). (где m — целое число, а n — натуральное число). Видно, что одновременно существует столько же натуральных чисел, сколько и целых. Количество (мощность) ряда натуральных чисел обозначается символом ℵ0 (Алеф Зеро).
Тот же трюк с числами не работает с бесконечными непериодическими дробями (иррациональными числами). Предположим, что такое множество измеримо. То есть, предположим, что его элементы могут быть пронумерованы натуральными числами. Теперь рассмотрим бесконечную дробь бесконечно малых с нулевыми целыми числами. Если первая цифра после запятой не равна цифре на том же месте в дроби №1, вторая цифра не равна цифре на втором месте в дроби №2 и т.д., то полученная дробь будет заведомо отличаться от каждой дроби хотя бы на одну цифру. Оказывается, в нашей бесконечной системе счисления такого числа нет! Доказательство прикладной формы называется диагональным методом Кантора, в честь математика Джорджа Кадора, который ее изобрел.
Не совершайте ошибку, записывая все бесконечные дроби как иррациональные числа. Неделимые числа — это только те, которые не могут быть выражены в виде непересекающихся пропорций в формате m/n. В таблицах дробей дроби 1/3 и 2/7 также бесконечны, но «неопытность» зависит от выбранной числовой системы. Например, в основании 21 дробь 1/2 конечна, а дробь 1/2 бесконечна (журнал).
Говорят, что бесконечное множество дробных дробей имеет мощность непрерывных дробей, обозначаемую символом ℵ.1 (Алеф 1). Далее необходимо использовать следующие наборы следует рассмотреть алфавит (конечный набор символов). В настоящее время алфавит a* представляет собой множество всех конечных цепочек символов. Поскольку алфавит конечен и каждая цепочка конечна, все эти цепочки измеримы (их можно посчитать по натуральным числам).

Насколько велико конечное число?
Предположим, что алфавит содержит все изобретенные на Земле символы, такие как русский алфавит, японские иероглифы и шумерская клинопись. Тогда наше целое включает в себя все книги, которые когда-либо были написаны, все книги, которые когда-либо будут написаны, и все книги, которые никто никогда не напишет (например, хаотичные последовательности персонажей). В конце концов, представьте себе книгу толщиной с Солнечную систему, с диагоналями листов, равными диаметру галактики, и написанную двенадцатым шрифтом. Набор, который мы придумали, будет включать все эти книги, а также по крайней мере одного персонажа, отличного от них, потому что вселенная бесконечна! Кто мешает нам представить себе книги размером в миллиарды световых лет? И все эти книги? Уже на этом этапе воображение может дать сбой, и, наконец, наши цифры поддаются измерению. Чтобы завершить толпу сиквелом, мы должны рассмотреть бесконечное количество книг, по сравнению с которыми предыдущая книга — детская игрушка. Но даже одной бесконечной книги нам недостаточно; мы должны посмотреть на все бесконечные книги. Мы должны просмотреть все бесконечные книги.
Мы выяснили, почему алгоритм не может иметь конкретного определения. Однако можно определить свойства, которыми должен обладать каждый алгоритм. К сожалению, в литературе часто путают обязательные и необязательные свойства. Давайте рассмотрим это более подробно.
Обязательные свойства
Начнем с обязательных свойств. Алгоритм можно описать как конечный текст, состоящий из конечного числа буквенных символов. Действительно, невозможно написать бесконечный текст в чисто технических терминах. Алгоритм также не может быть бесконечным, как это относится к строительной деятельности. Способность описать алгоритм как конечный текст можно назвать объективностью и свойством конечности.
Еще одним очевидным свойством алгоритмов является их дискретность. Независимо от исполнителя, выполнение алгоритма является отдельным процессом и анализируется в основном действии. Дискретность можно также понимать в том смысле, что информация, над которой работает алгоритм, может быть выражена в виде текста.
Третье основное свойство алгоритма называется детерминизмом. Она заключается в том, что существует только один способ выполнения предписанной процедуры. Единственное, что потенциально может повлиять на процесс выполнения, — это входные данные, но при одних и тех же входных данных алгоритм всегда будет выдавать один и тот же результат.
Эти три свойства являются общими для всех алгоритмов. Если мы нарушаем хотя бы один из них, мы больше не являемся алгоритмом. Даже если вы уже на грани фола, вы можете добавить читаемость реализатора к необходимым свойствам. В большинстве случаев это относится не к самому алгоритму, а к его символизму.
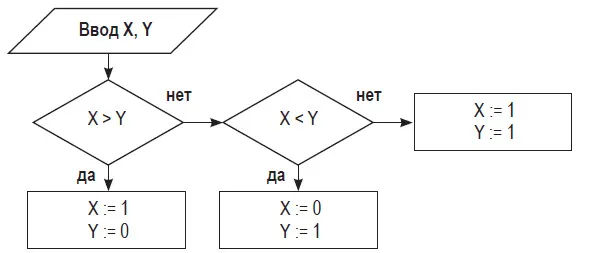
В том же компьютерном справочнике свойство ‘vinaigrette’.
Необязательные свойства
В дополнение к обязательным свойствам алгоритм может иметь некоторые специальные свойства, которые вовсе не являются обязательными. Давайте начнем с масс. Конечно, вам нужен алгоритм, который решает рассматриваемую категорию на основе входных данных. Однако существуют алгоритмы, которые вообще не зависят от входных данных, например, хорошо известный вывод ‘Hello world’. Подобно тому, как между вычислимыми функциями существуют фиксированные функции, между алгоритмами существует единый источник результатов.
Теперь рассмотрим распространенное мнение о том, что алгоритмам необходимы свойства корректности и полноты. Давайте начнем с корректности. Это качество не может быть формализовано, так как не существует стандарта для его правильности. Действительно, многие сталкивались с ситуациями, когда разработчик считает программу правильной, а клиент — нет. Когда дело доходит до полноты, ситуация становится более интересной. Рассмотрим термин «применимость». Алгоритм, заданный ключевым словом, называется применимым к слову, если он завершается за конечное число шагов. Самое интересное, что проблема применимости не может быть решена алгоритмически. То есть, невозможно создать алгоритм, который по входным данным и входным словам алгоритма определяет, завершится ли он за конечное число шагов. Ничто не мешает вам создать программу, состоящую только из одного бесконечного цикла. И эта программа все еще является алгоритмом.
Заключение
Иногда мир оказывается немного сложнее, чем нам хотелось бы. Существующие формы алгоритмической теории — это всего лишь абстрактные математические системы, такие как геометрия Евклида или теория вероятности, но понятие вычислимости лежит за пределами математики и является свойством нашей Вселенной, наряду со скоростью света и универсальным законом гравитации. Ответить на вопрос об алгоритмах и вычислимости, вероятно, невозможно, но попытка найти ответ на этот вопрос оказалась более ценной, чем бесспорный ответ.
Содержание этой статьи в основном основано на первом томе книги «Программирование: введение в профессию», написанной А. -В. Столярова.Для тех, кто хочет больше узнать об алгоритмах и теории вычислимости, в дополнение к этой книге рекомендуем книгу «От Диофанта до Тьюринга» Босса Б. и третий том по математической логике и теории алгоритмов А. Шена.
Центр обработки данных ITSOFT — размещение и аренда серверов и стоек в двух центрах обработки данных в Москве. 100% UPTIME в последние годы. Хостинговая GPU-ферма и ASIC-майнер, GPU-серверы в аренду, лицензии на связь, SSL-сертификаты, управление сервером и поддержка сайта.