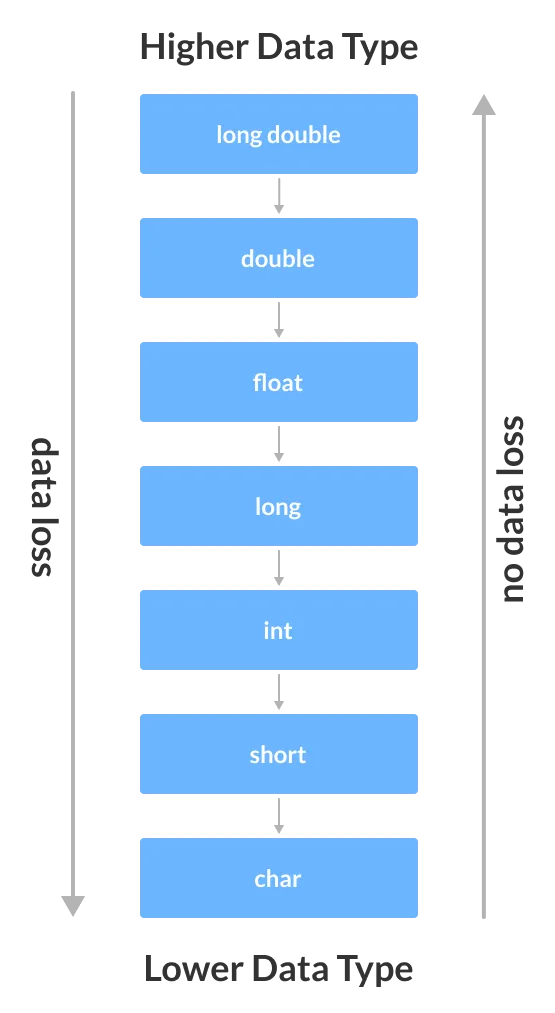
Google использует префикс 0x, чтобы отличать шестнадцатеричные числа от всех остальных чисел. Чтобы перевести 121 в восьмеричное число, введите запрос 121 Octal.
Системы счисления
В этом руководстве мы рассмотрим числа, поскольку разработчики используют странные способы написания чисел и их интерпретацию.
С древних времен люди нуждались в записи чисел. В торговле цифры необходимы для того, чтобы знать, сколько товаров имеется на складе и сколько денег зарабатывает торговая компания. Записи небесных сидений помогли шумерам составить первые календари, а календари помогли им заранее подготовить посевную и сбор урожая. Оценки зданий, перепись населения, распределение наследства — оказались востребованными даже в самых старых государствах.
Таким образом, люди записывали номера за многие годы. Цифры были маленькими и легко записывались с помощью насечек или зарубок, но если цифра состояла более чем из одной буквы, требовалась отдельная система записей. В разных странах эта проблема решалась по-разному.
Различные способы записи чисел известны как числовые системы.
Было изобретено много цифр, а две древние даты используются и сегодня. Римская система нумерации пришла из Рима, где числа записывались из Рима. Римляне приобрели количество пальцев на одной руке — 5, а основание обеих рук. Используя их. Например, VII — 7, а XIX — 19.
От древних шумеров мы научились делить дроби на 60 мест. Для них существует 60 минут времени и 60 секунд в минуте. Шумерская система счисления называется шестнадцатеричной. Но, конечно же, самая известная числовая нотация, похоже, была изобретена в Древней Индии. Сейчас она называется арабской или десятичной системой счисления.
От десятичных чисел к двоичным
В качестве примера того, как работает десятичная система, рассмотрим произвольные большие числа.
Это четырехзначное число, потому что оно состоит из четырех цифр. Десятичная система также допускает десять различных чисел.
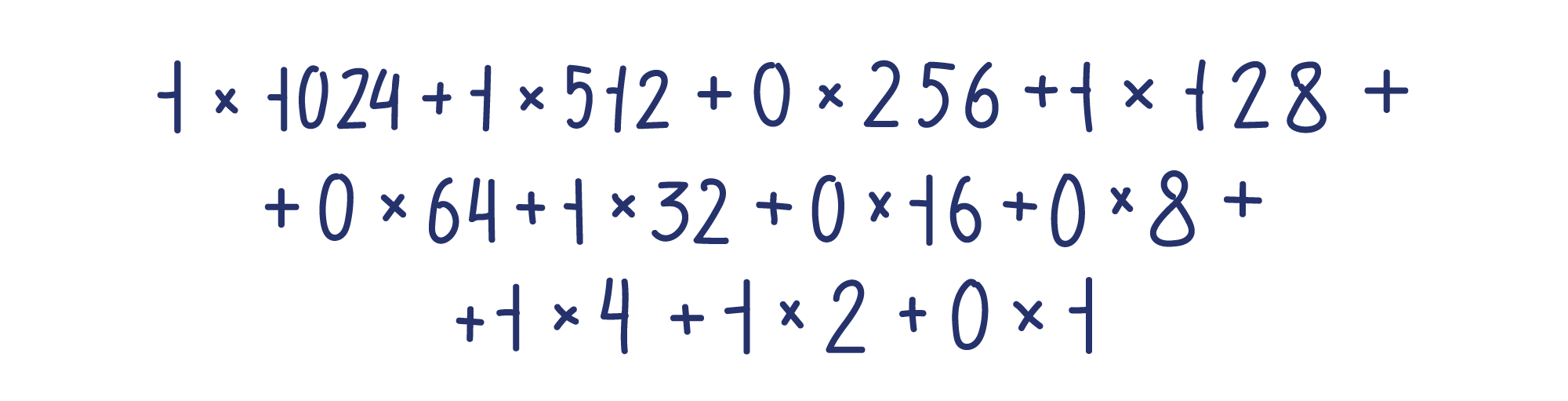
Значение каждого числа зависит от его положения. Поэтому эту систему счисления также называют позиционной системой. В правой части после сотен, десятков чисел пишутся единицы. Символика 1702 буквально означает следующее.
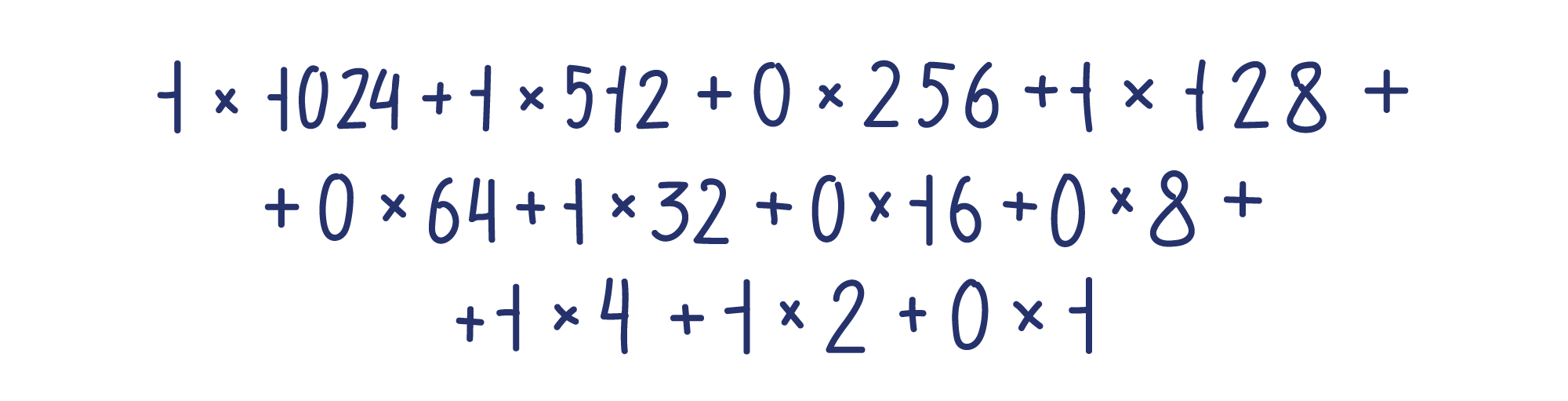
Числа, написанные на соседних участках, отличаются на 10. Это десятичная система. Однако, как мы уже говорили, привычная нам десятичная система не является единственной. Однако принципы других систем символизма можно легко понять. Например, чтобы записать то же число 1702 в двоичной системе, нужно следовать тем же правилам, но только с 2, 0 и 1 вместо 10 цифр.
Числа, записанные в соседних позициях, будут отличаться на один коэффициент 2, а не на один коэффициент 10. Так, если десятичная система показывает 1, 10, 100, 1,000, 10,000, то двоичная система имеет 1, 2, 4, 8, 16 и т.д.
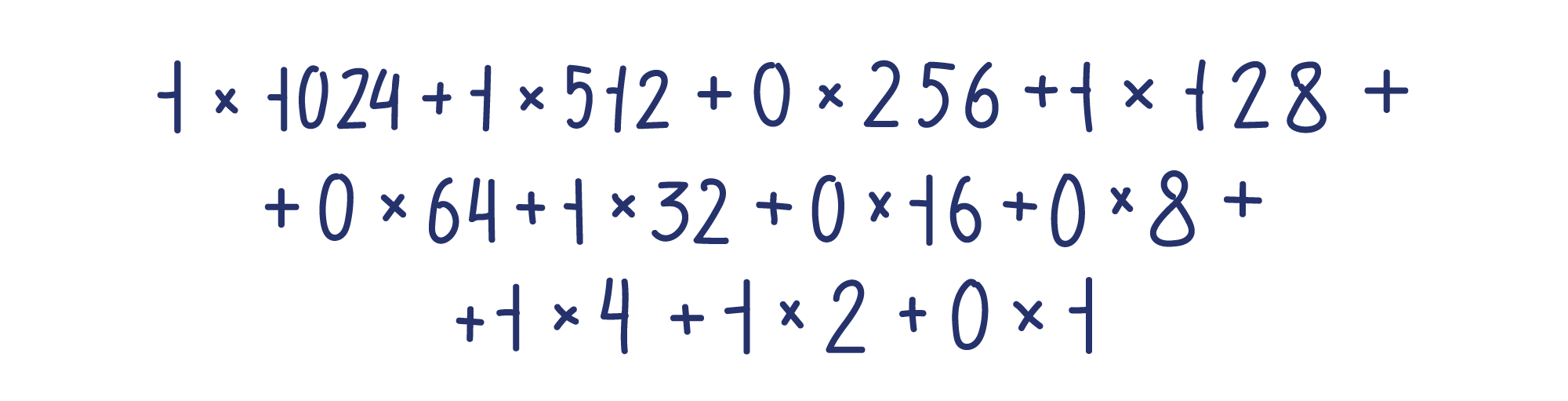
Это очень большие двоичные числа. Давайте запишем его в нормальной форме.
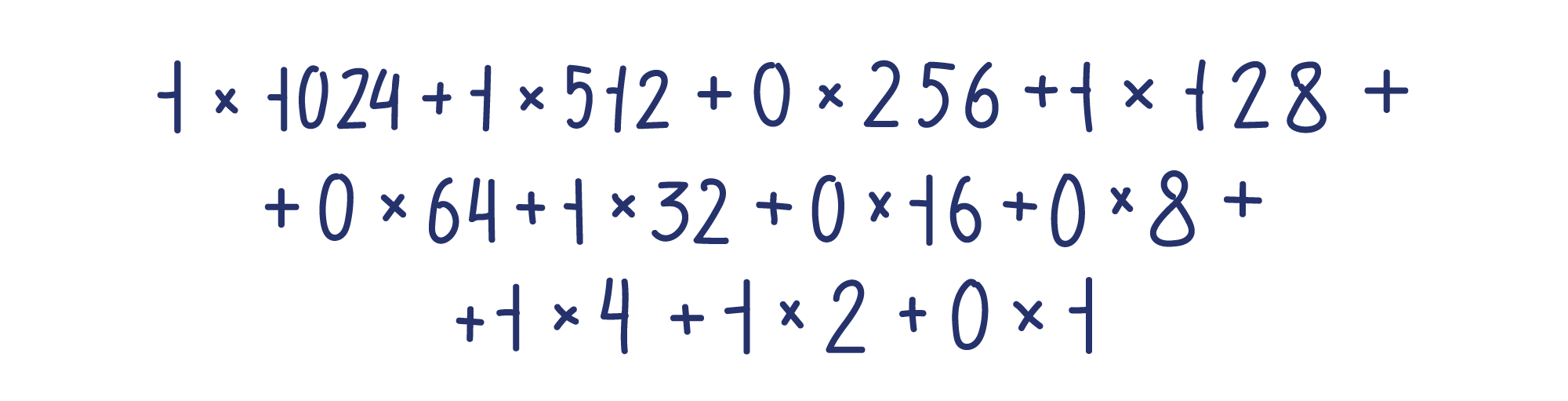
Это число может быть очень большим десятичным числом, потому что оно состоит из одних цифр. Чтобы отличить двоичные числа от десятичных, они имеют основание системы счисления. А именно, 2.
Это особенно важно, когда в тексте одновременно отображаются десятичные и двоичные числа.
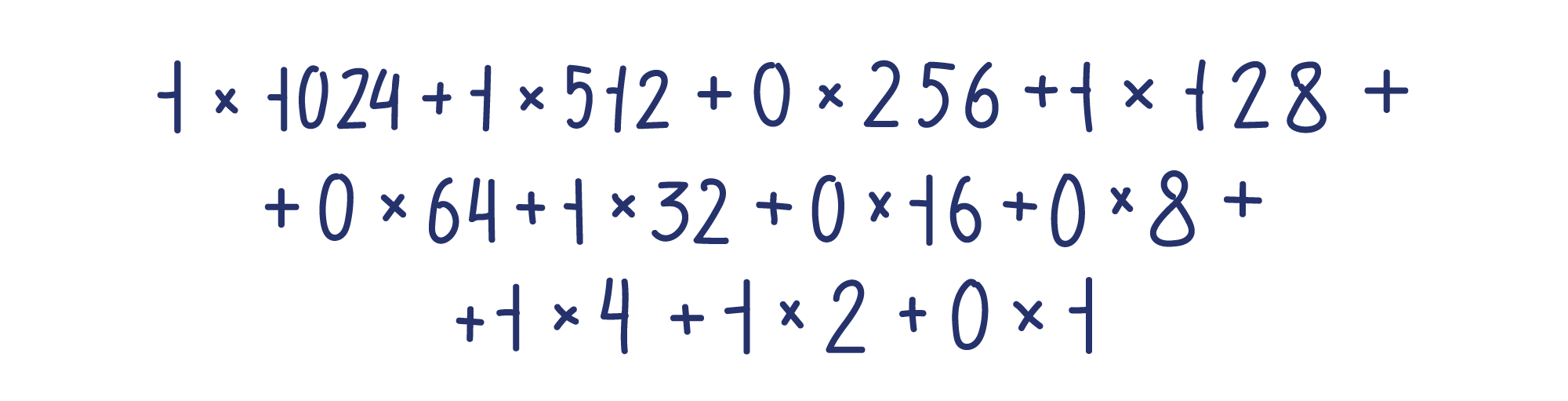
Зачем нужна двоичная система
Бинарные системы кажутся очень редкими, а числа, описанные в них, огромны. Почему это необходимо? Разве компьютеры не могут работать с привычными нам десятичными системами?
Оказывается, раньше они точно работали. Eniac, первый компьютер, разработанный в 1945 году, хранил числа в десятичной таблице. Для хранения каждой цифры использовалась схема, называемая кольцевым регистратором, которая состояла из десяти радиоэлементов.
Для записи всех чисел от 0 до 999 999 вплоть до миллиона требуется шесть цифр, поэтому для хранения этих чисел необходимо до 60 ламп.
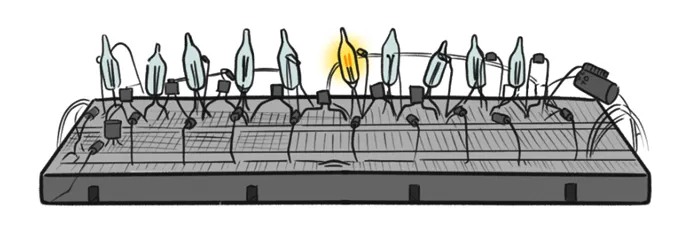
Инженеры поняли, что если закодировать числа в двоичной системе, то для хранения одного и того же числа три раза потребуется всего 20 радиоламп.
Первое преимущество двоичных чисел — это простота схемы. Второе, менее важное, — это скорость. Добавление числа, хранящегося в кольцевом регистраторе, требует до 10 тактов процессора на каждую операцию. Добавление двоичных файлов может быть в десять раз быстрее в тактовых циклах.
Группа инженеров, создавших первые компьютеры, в 1946 году опубликовала статью, в которой обосновала преимущества двоичной системы для компьютерных чисел. Первым среди авторов был назван американский математик Джон фон Нейман. Поэтому сейчас дизайн компьютера называют архитектурой фон Неймана, что не совсем справедливо по отношению к другим изобретателям компьютеров.
С символизмом двоичных чисел трудно справиться при разработке программ. Компьютер сам преобразует двоичные числа в десятичные и наоборот по большей части. Можно долго писать код, не понимая, что данные хранятся в компьютере особым образом.
Зачем изучать двоичную систему, если всю работу делает компьютер? Разработчикам необходимо создавать программы, которые работают непосредственно с материалом. Например, разработчикам игрушек необходимо знать, как работают видеокарты, чтобы сделать компьютерную графику быстрее. Аналогично, разработчик операционной системы должен понимать, как производятся данные, чтобы их хранить.
Программы, которые выполняются непосредственно на материале, называются низкоуровневыми системными программами или программами. Эти программы требуют от разработчиков понимания того, как работают компьютеры. Поэтому изучение арифметических систем позволяет разработчикам расширить свои навыки и стать более осведомленными в целом.
Поэтому им необходимо понимать двоичную систему счисления, чтобы они могли создавать сложные системные программы.
Давайте рассмотрим, как быстро преобразовать двоичное число в десятичное. В данном примере нам нужно двоичное число настолько большое, что его невозможно вычислить пальцами.
Как перевести число из двоичной системы в десятичную
Проблемы с системами счисления часто требуют перевода чисел из двоичной системы в десятичную. Для выполнения этой задачи используется алгоритм преобразования двоичных чисел в десятичные.
- Пронумеровать разряды двоичного числа справа налево, начиная с нуля.
- Умножить каждый ненулевой разряд на 2 в степени его номера и сложить результаты.
Онлайн калькулятор перевода чисел из одной системы счисления в любую другую
Преобразование числа 1111001102 Двоичный перевод в десятичный.
Сосчитайте цифры числа справа налево, начиная с нуля.
| 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
1111001102 = 1⋅28 +1⋅27 +1⋅26 +1⋅25 +1⋅22 + 1 nal2 1 = 256 + 128 + 64 + 32 + 4 + 2 = 48610
Преобразование числа 1010001112 Двоичный перевод в десятичный.
Справа налево от номера числа:.
| 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
1010001112 =1⋅28 +1⋅26 +1⋅22 +1⋅21 +1⋅20 = 256 + 64 + 4 + 2 + 1 = 32710
Если вам понравился этот материал и вы считаете его полезным, поделитесь им со своими друзьями!
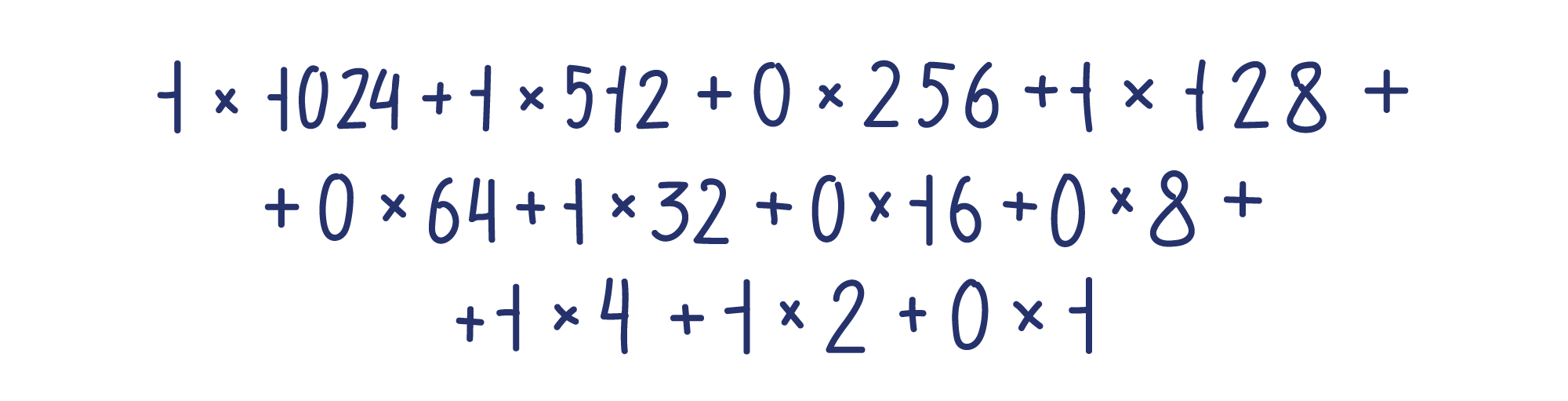
Ведра — это емкости для хранения и транспортировки жидкостей и сыпучих материалов на небольшие расстояния.
Что касается нас.
На нашем сайте вы найдете множество полезных калькуляторов, инверторов, таблиц и справочных материалов для базового сектора.
Самый простой способ подсчета — использовать соответствующие онлайн-инструменты. Используйте поиск, чтобы найти нужный инструмент на нашем сайте.
calcsbox.com.
На этом сайте используется технология латекса. Поэтому, пожалуйста, дождитесь полной загрузки страницы и корректного отображения типа и формулы.
Компьютеры, работающие на десятичной системе, оказались сложными и медленными. Хранение числовых значений в двоичной системе позволяет использовать более простые схемы и более быстрые компьютеры.
Как перевести число из десятичной системы в двоичную
Эта задача числового перевода, как и предыдущая, имеет два решения.
Первый способ перевода предполагает, во-вторых, правильное знание разделения. Особенность этого метода в том, что при делении получается два возможных остатка — 0 и 1.
Следуя следующим правилам, число 156 переводится на машинный язык. Сначала сумма делится на два, а 78 уравновешивается нулем. Первый баланс записывается как двоичное значение. Результат снова делится на два, таким образом, баланс равен 39 с ответом ноль. Второй баланс описывается размером следующего класса. Половина числа 39 равна 19, что равняется остатку 1. Результатом является двоичное число 00111001.
Второй метод формирует числовую последовательность из результата увеличения числа 2, пока это значение не станет больше исходного. Таким образом, получаются последовательности из 128, 64, 32, 16, 8, 4, 2 и 1. Таким образом, судя по показаниям полученного ряда, деление 128 на 156 дает остаток. Первая цифра в двоичном числе — 1. Отнятие 128 от 156 дает ответ 28, и это число делится на следующее число в ряду. Таким образом, 26 делится на 64, что в остатке дает 0. Это следующее значение в двоичном коде. После выполнения всех действий вы получаете двоичное целое число 00111001_2.

Заключение
Понимание правил, по которым числа переводятся из одной системы в другую, является одним из ключевых элементов программирования. Однако нет необходимости вручную переводить числа или текст на машинный язык. Сейчас для этого существует множество онлайн-сервисов и настольных приложений. И по мере продвижения вперед основные ценности запоминаются. Помните, однако, что хорошее понимание основных принципов отличает начинающих разработчиков от экспертов.
В этом видео вы узнаете, как перевести двоичную систему счисления в десятичную.
Пожалуйста, ставьте лайк, это важно для наших авторов, подписывайтесь на наш канал на yandex.zen и присоединяйтесь к команде Вконтакте!
В древнем Вавилоне, примерно в I тысячелетии до н. э., использовалась система счисления, в которой числа ниже 60 долларов представлялись двумя цифрами.
Перевод чисел из восьмеричной системы в двоичную систему счисления.
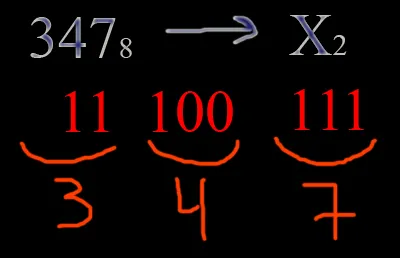
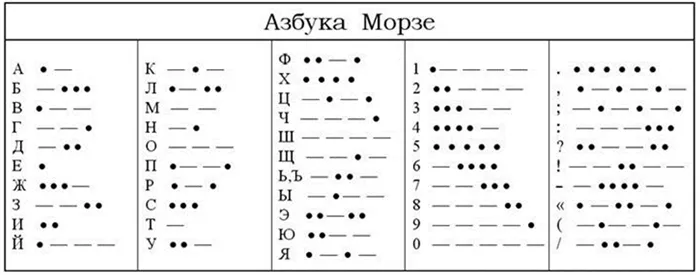
Мы делаем то, что делали раньше. Используя таблицу в верхней части статьи, проанализируйте каждое число в восьмеричной системе с тремя цифрами в двоичной системе. Нули в левой части отклоняются.
Перевод чисел из двоичной системы в десятичную систему счисления.
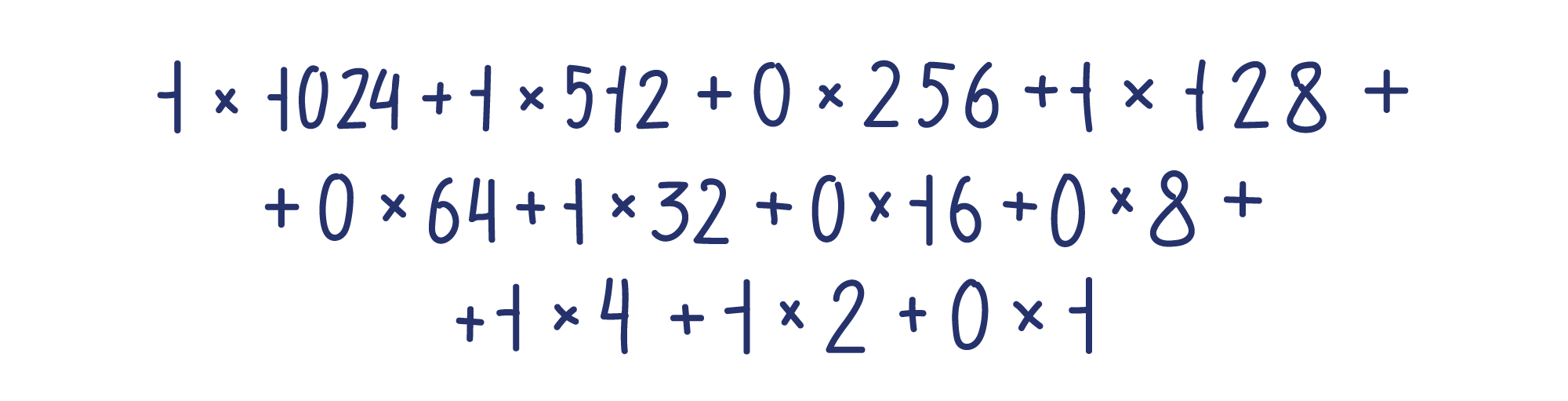
Мы берем двоичные числа, начиная с нижнего разряда (т.е. справа), и начинаем умножать их на два с соответствующей силой. Мощность начинается с нуля и увеличивается по одному. Все эти продукты суммируются.
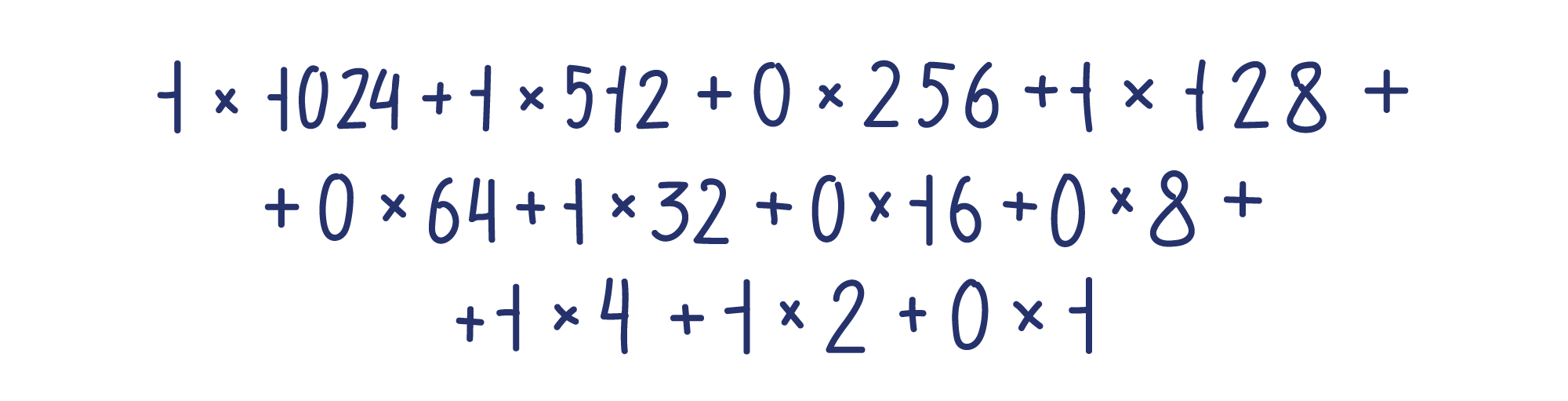
После вычисления вы получаете числа в десятичной системе.
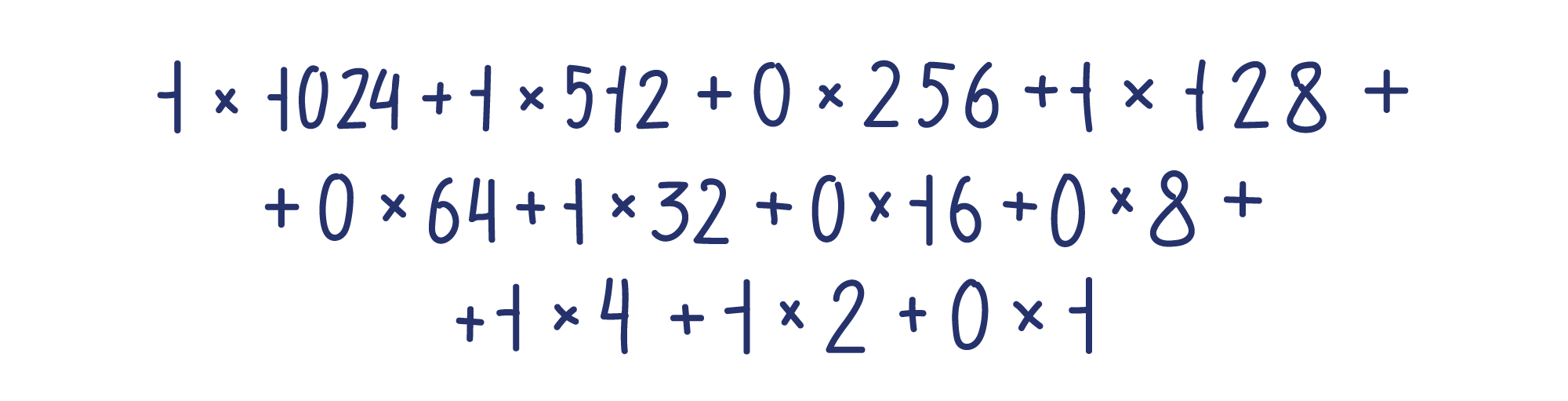
Результат — 11010011.2 — > 21110
Перевод чисел из шестнадцатиричной системы в восьмеричную систему счисления и обратно.
Переведите A10 из шестнадцатеричной системы в восьмеричную A1016-> X8 .
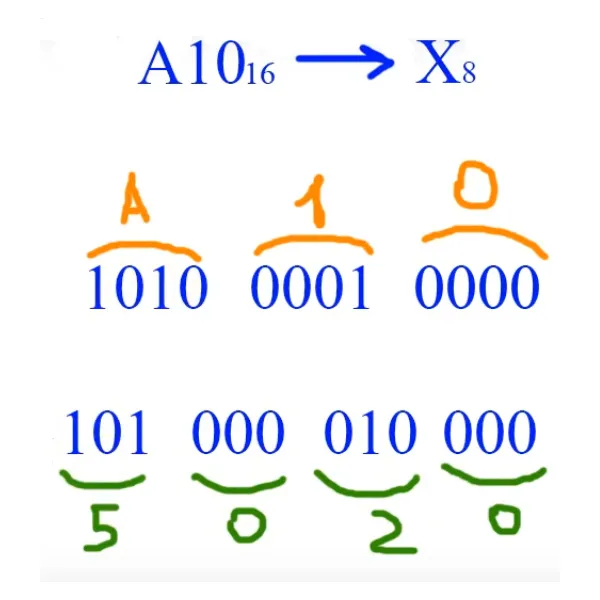
Из таблицы в начале статьи следует, что каждая цифра шестнадцатеричного кода делится на четыре цифры двоичного кода (т.е. число переводится в двоичный). Полученное число разбивается на три цифры, как показано на схеме, и затем число собирается в восьмеричную систему счисления. Повторите преобразование таким же образом, но в обратном порядке.
Преобразование числа из двоичной системы в десятичную или из десятичной системы в двоичную не является сложной задачей. Главное здесь — понять, какому алгоритму следовать. В нашем примере проиллюстрируем число «29», которое мы уже использовали.
Перевод чисел из одной системы счисления в другую
При переводе числа из одной системы счисления в другую удобнее сначала перевести его в десятичную систему, а затем перевести из десятичной системы в другую систему счисления.
Преобразование чисел из одной системы счисления в другую играет важную роль в компьютерной инженерии при использовании арифметических машин. Основные правила для этих преобразований следующие
При преобразовании двоичного числа в десятичное число двоичное число должно быть выражено в виде многочлена. Каждый элемент представлен как произведение цифры и соответствующей силы базового числа (в данном случае $ 3500). Затем многочлен вычисляется в соответствии с правилами десятичной арифметики.
$ X_2 = A_n \ cdot 2 ^ + A_ \ cdot 2 ^ + A_ \ cdot 2^+. + A_2 \ cdot 2 ^ 1 + A_1 \ cdot 2 ^ 0 $
При переводе, для удобства, рекомендуется использовать таблицу 1.
Переведите $11110101_2$ в десятичную систему счисления.
Решение. Используйте приведенную выше таблицу мощности $3500 на основе $400, чтобы представить это число в виде многочлена.
$ 1111110101_2 = 1 \ cdot 27 + 1 \ cdot 26 + 1 \ cdot 25 + 1 \ cdot 24 + 0 \ cdot 23 + 1 \ cdot 22 + 0 \ cdot 21 + 1 \ cdot 20 = 128 + 64 + 32 + 16 + 0 + 4 + 0 + 0 + 0 + 1 = 245_ $
Чтобы перевести число из октавной системы в десятичную, его нужно выразить в виде полинома. Каждый элемент представлен как произведение числа и соответствующей ему степени базового числа (в данном случае $8). Затем полином вычисляется с помощью правила десятичных чисел.
$ X_8 = A_n \ cdot 8 ^ + A_ \ cdot 8 ^ + A_ \ cdot 8^+. + A_2 \ cdot 8 ^ 1 + A_1 \ cdot 8 ^ 0 $
При переводе рекомендуется использовать таблицу 2.
Готовые работы на аналогичную тему
Переведите $75013_8$ в десятичную систему счисления.
Решение. Используйте приведенную выше таблицу мощности $3500, основанную на $8$, чтобы представить это число в виде многочлена.
$ 75013_8 = 7 \ cdot 8 ^ 4 + 5 \ cdot 8 ^ 3 + 0 \ cdot 8 ^ 2 + 1 \ cdot 8 ^ 1 + 3 \ cdot 8 ^ 0 = 31243_ $
Чтобы перевести число из шестнадцатеричной системы счисления в десятичную, его нужно выразить в виде полинома. Для вычисления полинома каждый элемент представляется в виде произведения числа и степени соответствующего базового числа (в данном случае $16). Используйте их; правило десятичных чисел:.
$ X_ = A_n \ cdot 16 ^ + A_ \ cdot 16 ^ + A_ \ cdot 16^+. + A_2 \ cdot 16 ^ 1 + A_1 \ cdot 16 ^ 0 $
При переводе рекомендуется использовать таблицу 3.
Переведите $FFA2_$ в десятичную систему счисления.
Решение. Используя приведенную выше таблицу, выразите число в виде многочлена, используя $3$ силы основания $8$.
$ FFA2_ $ = 15 \ cdot 16 ^ 3 + 15 \ cdot 16 ^ 2 + 10 \ cdot 16 ^ 1 + 2 \ cdot 16 ^ 0 = 61440 + 3840 + 160 + 2 = 65442_ $
Правила перевода чисел из десятичной системы счисления в другую
- Для перевода числа из десятичной системы счисления в двоичную его необходимо последовательно делить на 3500$ до тех пор, пока не останется остаток, меньший или равный 400$. Число в двоичной системе представить как последовательность последнего результата деления и остатков от деления в обратном порядке.
Переведите $22_$ в двоичную систему.
- Для перевода числа из десятичной системы счисления в восьмеричную его необходимо последовательно делить на $8$ до тех пор, пока не останется остаток, меньший или равный $7$. Число в восьмеричной системе счисления представить как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Переведите $571_$ в октавы.
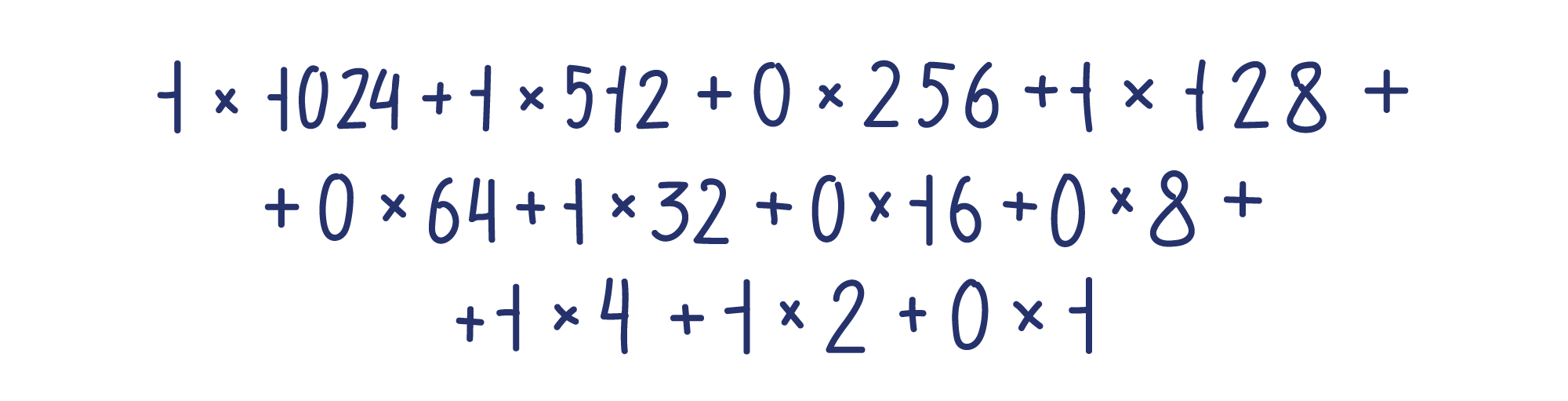
- Для перевода числа из десятичной системы счисления в шестнадцатеричную систему его необходимо последовательно делить на $16$ до тех пор, пока не останется остаток, меньший или равный $15$. Число в шестнадцатеричной системе представить как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Переведите $7467_$ в шестнадцатеричную систему.
Чтобы преобразовать правильную дробь из дробной системы счисления в нефракционную, дробную часть преобразуемого числа нужно умножить на основание преобразуемой системы. Фракция новой системы с самого начала представляется как весь продукт.
Например:
Правила перевода чисел из двоичной системы счисления в другую
- Чтобы перевести число из двоичной системы счисления в восьмеричную, его необходимо разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, затем каждую триаду заменить соответствующей восьмеричной цифрой согласно таблице 4.
Переведите $1001011_2$ в восьмеричную систему счисления.
Решение. Используйте таблицу 4 для перевода числа из двоичной системы в восьмеричную.
- Чтобы перевести число из двоичной системы счисления в шестнадцатеричную, его следует разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, затем каждую тетраду заменить соответствующей восьмеричной цифрой согласно таблице 4.
Переведите число $1011100011_2$ в шестнадцатеричную систему.
Разрешение. Используйте таблицу 4 для перевода числа из двоичной системы в шестнадцатеричную.
Восьмеричная форма .3125_$ означает .24_$.
Здесь может возникнуть проблема, когда конечная десятичная дробь может соответствовать бесконечной (циклической) дроби в недесятичной системе счисления. В таких случаях количество цифр дроби, представленной в новой системе, будет зависеть от требуемой точности. Также обратите внимание, что в любой системе счисления целые числа остаются целыми числами, а обычные дроби — дробями.
Как следует из названия, эта система основана на числе 16. Поскольку это позиция, значение каждой позиции в 16 раз больше предыдущей. По логике, требуется 16 чисел. Первые десять — 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Кроме того, для обозначения букв используются буквы алфавита.
Онлайн конвертер систем счисления, перевод между десятичной, двоичной, восьмеричной и другими системами
С древних времен люди использовали различные методы и измерения. Они постоянно меняются и совершенствуются, адаптируясь к текущим потребностям. Сегодня десятичная система счисления является общепринятой, но используются и другие обозначения. Наиболее часто используемыми, особенно в программировании, являются двоичный, восьмеричный и шестнадцатеричный форматы. Онлайн-конвертеры систем нумерации быстро преобразуют различные номера из одной системы в другую.

Первые системы счисления
С момента появления торговли людьми возникла необходимость подсчета. Первоначально это была система банкнот в виде палочек и каменных зарубок. Позже он был усовершенствован и стал более сложным. Гораздо проще считать информацию устно, чем записывать ее. Однако со временем появились признаки того, что его можно использовать для записи информации.
Самой примитивной системой нумерации является номер единицы измерения. Существует только один символ. Все последовательные числа образуются путем простого повторения.
По сути, это была беспозиционная нотная система, в которой каждая цифра имела свой символ.
Неположительная система построена таким образом — она имеет отдельные символы для разных чисел и последовательные символы для кратных им. Числа создаются путем добавления символов.
Уже в третьем тысячелетии до нашей эры в Египте начали использовать иероглифы для обозначения чисел. Примерно в то же время Древняя Греция использовала буквы своего алфавита для записи чисел. И это была первая буква в названии числа: число.
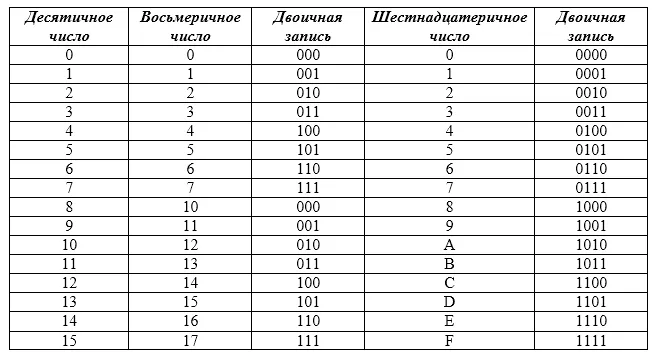
| знак | значение | название |
| Ι | 1 | ἴος «иос» |
| Π | 5 | πέντε «пенте» |
| Δ | 10 | δέκα «дека» |
| Η | 100 | ἑκατόν «хекатон» |
| Χ | 1 000 | χίλιοι «хилиой» |
| Μ | 10 000 | μύριοι «мюриой» |
Древний Рим также создал свои собственные записи чисел. Уже в то время были сформулированы правила создания новых чисел и их использования для выполнения различных операций, таких как сложение, дополнение, вычитание и деление. Была создана первая система счисления.
Система счисления — это способ записи чисел и набор правил, которые позволяют выполнять различные математические операции с числами.
Каждая система имеет набор символов, используемых для записи чисел. Эти символы являются цифрами. Их можно комбинировать различными способами, создавая бесконечное количество комбинаций.
Счет в Древнем Вавилоне
Достижения вавилонских ученых требуют особого внимания. Уже 4000 лет назад они создали первую в мире систему счисления. Это было основано на использовании двух точек с вертикальным клином в один и горизонтальным в десять.
То, как была создана система нумерации, наглядно показано на схеме.

В шестнадцатеричной системе первые числа состояли из цифр от 1 до 60, что являлось основанием. Шестьдесят единиц из первого разряда образовали второй разряд, а 60 точек из второго разряда образовали третий разряд. Этот метод измерения был разработан на основе системы Додеканеса-Сумериана.
Шестнадцатеричная система используется и сегодня, поскольку она очень гибкая и точная. Эта система использовалась вавилонскими учеными для систематизации времени и лета. Их год состоял из 360 дней и 60 минут.
Современные система счисления
Сегодня мы все используем системы позиционирования. Они функционируют следующим образом.
- Использование ограниченного количества цифр, которые имеют последовательные значения 0, 1, 2,… Это никоим образом не ограничивает размер записываемых чисел.
- Каждой позиционной системе присваивается определенное значение, которое мы называем базой. Количество цифр равно базовому значению. Для десятичной системы у нас есть набор из 10 цифр, потому что база равна 10. В шестеричной системе цифр будет 6. В системах с основанием больше 10 нужно больше цифр, чем определено для десятичной системы. Эта проблема решается просто — для записи чисел комбинируют цифры и буквы латинского алфавита. Например, для двенадцатеричной системы берут двенадцать символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. Цифра A равна 10, а цифра B =11.
- Значение цифры в записи зависит от ее положения, отсюда и название « позиционная система». Каждой из них присваивается вес. Он равен последовательным базовым мощностям, отсчитываемым справа.
- Значение числа в обозначении позиции рассчитывается как сумма произведений цифр на веса их позиций.
Десятичная система
Для большинства из нас естественным способом представления чисел является десятичная система. Мы учимся считать с детства. Это основа для преподавания математики в школе, и мы используем их в повседневной жизни. В десятичной системе используется десять символов для представления чисел ноль, один, два, три, четыре, пять, шесть, семь, восемь, восемь и девять. Они обозначаются как ноль, один, два, три, четыре, пять, шесть, семь, восемь и девять. Отсюда и названия.
Десятичные дроби чисел были созданы много веков назад. Предположительно, это связано с десятью пальцами. Эта система позволяет просто и рационально представить любое число, независимо от его размера, а также легко выполнять все арифметические операции. Десятичная система — самая распространенная система, использовавшаяся в истории.

Двоичная (бинарная) система
С развитием компьютерных технологий техническим устройствам стало очень трудно использовать такое большое количество символов. Это нашло практическое применение в других системах счисления, отличных от десятичной системы. В информатике двоичная нумерация чисел занимает первое место. Они также известны как двоичные файлы, но реже их называют «нулевыми».
В двоичных измерениях используются только два числовых значения — «0» и «1». Этот набор — лучший способ записать любое число.
Первое число — 0 (ноль), такое же, как и в других системах.
Следующее число — 1 (один). Это число также присутствует в двоичной системе и записывается как 1. Следующее число — 2 (два). В двоичном числе такого числа нет, поэтому оно добавляет еще одну позицию, смещенную вправо, но равную нулю. Поэтому второе десятичное число записывается как ’10’.
Следующее число из десятичной системы в двоичную выглядит следующим образом
- 3 — записываем, как «11»,
- 4 — «100»,
- 5 — «101»,
- 6 — «110»,
- 7 — «111»,
- 8 — «1000»,
- 9 — «1001» и т.д.
Начало всегда одно и то же. Двоичные цифры (0 или 1) называются битами. Название bit происходит от двоичной цифры в английской терминологии. Отсюда и второе название — двоичная система. Оно содержит только 0 и 1, но любое число может быть записано в двоичной форме. Если вам нужен простой перевод, чтобы избежать ошибок, используйте конвертер системы счисления.