Если масса пули равна 50 г, а масса деревянной мишени — 10 кг, то после попадания шара мишень отклоняется и поднимается на максимальную высоту 0,5 м. Заменяет вышеуказанные типы значений:.
Импульс тела, закон сохранения импульса
Единицей импульса является килограмм на метр на метр (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓V), так как масса всегда положительна (m> 0).
Пример 1. Определите импульс массы массой 10 г, запущенной со скоростью 300 м/с. Пренебрегайте сопротивлением воздуха.
Толчок сферы является произведением ускорения ее массы. Перед выполнением расчета единицы измерения необходимо перевести в СИ.
Относительный импульс
Момент — это векторная натуральная величина, равная произведению веса на относительную скорость.
p1TN2 — Движущая сила первого тела по сравнению со вторым телом, m1 — масса первого тела, v1TN2 — скорость первого тела по сравнению со вторым, v1 и v2 — Это скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример № 2. Два автомобиля одинаковой массы (15 т) движутся друг за другом по одной прямой. Первый имеет скорость 20 м/с, а второй — 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Переведите первую единицу в СИ:.
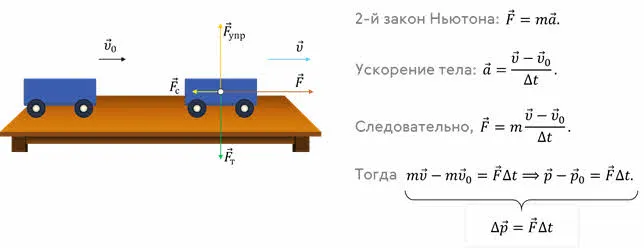
Изменение импульса тела
D P — изменение выталкивающей силы тела, P — конечный импульс тела, P0 — начальный импульс тела.
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар
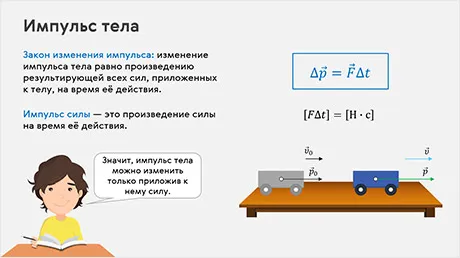
Единицы изменения импульса тела равны единицам первоначального импульса.
Абсолютно упругий удар

Единицы конечной и начальной скорости равны:.
Конечная и исходная единицы импульса равны:.
Мера изменения импульса тела равна удвоенной мере первоначального (конечного) импульса.
Пуля пробила стенку
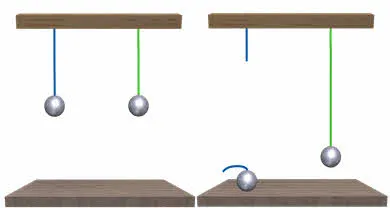
Мера изменения импульса тела равна разности между начальной и конечной мерами импульса.
Радиус-вектор тела повернул на 180 градусов
Мера изменения импульса тела равна удвоенной мере первоначального (конечного) импульса.
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
Единицы конечной и начальной скорости равны:.
Конечная и исходная единицы импульса равны:.
Угол падения равен углу отражения.
Мера изменения импульса в этом случае определяется уравнением.
Пример №3. Пак ударяется о неподвижную стену с абсолютной упругостью. Направление движения Пака изменилось на 90 градусов. Импульс шарика перед ударом равен 1 кг м/с. Какой коэффициент изменяет импульс пака в результате удара? Переведите ответ в одну десятую.
В данном случае 90 градусов — это 2a (угол между исходным импульсом и конечным импульсом), а A — угол между вектором импульса и нормалью. Для абсолютно упругого отражения предположим, что конечный импульс и числитель начального импульса равны.
Вычисляем:
Строго говоря, математическая формулировка второго закона Ньютона применима, когда сила, действующая на тело во время его действия, постоянна, т.е. не изменяется ни на одну из величин.
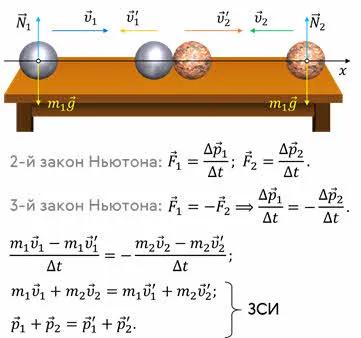
Импульс системы тел. Закон изменения импульса
Импульс (количество движения) механической системы — это вектор, равный сумме импульсов всех материальных точек системы.
Законы изменения и сохранения импульса являются следствием второго и третьего законов Ньютона.
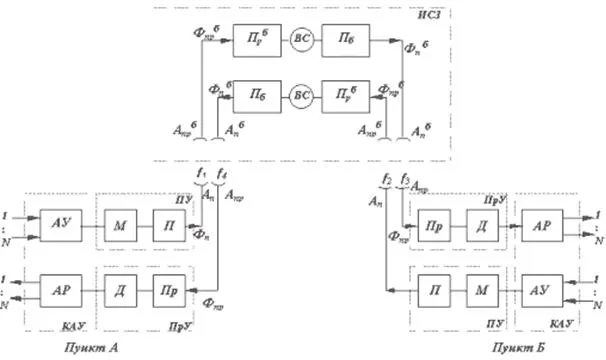
Рассмотрим систему, состоящую из двух тел. Силы ($ f_ $ и $ f_ $ на диаграмме. Органы системы взаимодействуют друг с другом.
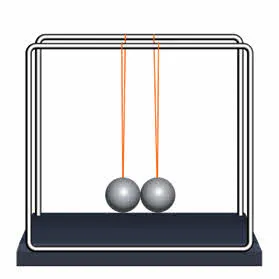
$$$ и $$$ действуют сами на себя внешние силы, действующие в системе, за исключением внутренних сил. Для каждого тела уравнения $Δp = fdt $. Складывая левую и правую части этих уравнений, получаем
В левой части мы имеем геометрическую сумму изменения импульса всех тел системы, равную изменению импульса самой системы -$> $. Вы можете написать $:.
Здесь $ f $ — это сумма всех внешних сил, действующих на тело. Результирующий эффект означает, что только внешние силы могут изменить импульс системы и что изменения в импульсе системы направлены так же, как и общие внешние силы. В этом заключается суть закона изменения импульса механической системы.
Внутренние силы не могут изменить общий импульс системы. Они могут изменить только импульс отдельных тел системы.
Закон сохранения импульса
Уравнение $> = fdt $ приводит к появлению момента импульса. Если на систему не действует внешняя сила, то правая часть уравнения $> = fdt $ обнуляется, и поэтому полный момент системы остается неизменным.
Система, в которой внешние силы не действуют или результирующая внешняя сила равна нулю, является замкнутой.
Метод сохранения импульса заключается в следующем.
Общий импульс замкнутой системы тел остается постоянным по отношению к взаимодействию тел системы между собой.
Полученные последствия применимы к системам, содержащим любое количество тел. Если суммарная внешняя сила ненулевая, но суммарная проекция в любом направлении равна нулю, то показатель импульса системы в этом направлении остается неизменным. Так, например, система тел на поверхности Земли не может считаться замкнутой из-за действующих на все тела гравитационных сил, но сумма проекций импульса в горизонтальном направлении может оставаться неизменной (если нет трения, ) как в этом направлении, но не действуют гравитационные силы.
Реактивное движение
Давайте рассмотрим несколько примеров, подтверждающих справедливость импульса импульса.
Возьмите детский резиновый шарик, надуйте его и отпустите. Когда воздух начнет выходить в одном направлении, вы увидите, что сам воздушный шар летит в другом направлении. Движение воздушного шара является примером реактивного движения. Это объясняется законом сохранения импульса: суммарный импульс «шарика и воздуха в нем» до движения воздуха равен нулю, а во время движения — поэтому шарик движется в обратном направлении. направлении потока и с такой скоростью, чтобы его импульс равнялся сплющиванию воздушного пучка.
Возвратно-поступательное движение — это движение тела, возникающее, когда часть тела покидает его с некоторой скоростью. По закону сохранения импульса, направление движения тела противоположно движению отделившейся части.
Ракетный полет основан на принципе реактивной тяги. Современные космические ракеты — это очень сложные летательные аппараты. Масса ракеты состоит из массы рекламного тела (т.е. горячих газов, образующихся при сгорании топлива и запускаемых в виде струи) и конечной или «сухой» массы ракеты. и остается после запуска с ракеты.
Когда из ракеты на большой скорости выпускается струя газа, сама ракета движется в противоположном направлении. Согласно закону сохранения импульса, импульс $ m_.
y_p $ прирост ракеты должен быть равен $ m_-y сжигаемого газа.
Появляется скорость ракеты.
Этот тип указывает на то, что скорость пусковой установки настолько велика, насколько велико отношение скорости пущенного газа к конечной («сухой») массе массы топлива (т.е.
Тип $ y_p = (>/)-y_ $ является приближением. При этом не учитывается, что по мере сгорания топлива масса ракеты по мере ее полета становится все меньше. Точный тип ракетной скорости возник в 1897 году К. Э. Циолковским и получил свое имя.
Тип Циолковского позволяет рассчитать количество топлива, необходимого для придания ракете определенной скорости.
Работа силы
Термин «работа» был введен в физику французским ученым Ж. Понселе в 1826 году. В повседневной жизни только человеческий труд называют работой, но в физике и, в частности, в технике, работа рассматривается как действие силы. Физическая стоимость труда обычно обозначается буквой $ a $.
Работа силы — это мера действия силы, в соответствии с ее измерением и адресом, а также перемещение точки приложения силы. Для постоянной мощности и прямолинейного сдвига проект определяется уравнением
где $ f $ — сила, действующая на тело, $ ΔR $ — перемещение, $ a $ — угол между силой и перемещением.
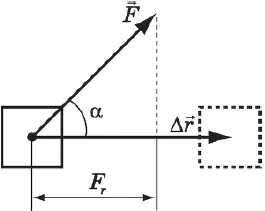
Работа мощности равна произведению коэффициентов мощности и перемещения и косинуса между ними, т.е. масштабному произведению $ f $ и $ и $.
На участках 0-1 импульс тела не изменялся. Таким образом, в этот момент тела двигались одинаково. В разделе 1-2 импульс тела увеличивался с помощью линейной функции, поэтому в этом разделе тела движутся с одинаковым ускорением.
править Импульс в релятивистской механике
Определение импульса было изменено в некоторых теориях относительности, поэтому он остается неизменным в относительных преобразованиях и определяется как четырехкомпонентный или четырехтрехмерный вектор.
Математика p^i = \ слева (⌘ frac, p_x, p_y, p_z \ справа) /Математика
Maths c / Math — скорость скорости света, если Math e / Math — полная энергия системы, Math ǫ mathbf
/math — пространственный вектор, соответствующий «нормальному» импульсу в релятивистских условиях.
Математика импульса ˈ mathbf
/математика массивных частиц
В релятивистской механике выражение импульса для v = C является бесконечно равным, если масса ненулевая. Поэтому частица с ненулевой массой может двигаться только со скоростью, меньшей скорости света.
Четырехчленная математика p^i /math связана с четырехчленной математикой u^i /math p^i = mcu^i /math. Учитывая соотношение maths u^iu_i = 1 /math, может возникнуть связь между энергией и импульсом тела.
Этот тип показывает, что объекты с нулевой массой, такие как фотоны, также имеют импульс, равный p = e/c. где e — энергия фотона, а c — скорость света.
При переходе в другие инерциальные системы отсчета импульс изменяется в соответствии с типом преобразования Лоренца.
В некоторых теориях относительности взаимодействие распространяется с конечной скоростью, которая не может превышать скорость света в вакууме. Это означает, что импульс, излучаемый лепестком, не сразу передается другим лепесткам и, следовательно, общий импульс всех частиц не сохраняется. Закон сохранения выполняется и в случае, когда толчок принадлежит полю — носителю взаимодействия, принадлежащему плотности толчка и плотности потока.
править Импульс в квантовой механике
В квантовой механике импульс определяется как оператор формы волны. Это противоречит гамильтоновой системе, поддержание которой обусловлено однородностью пространства. Принцип неопределенности Гейзенберга устанавливает предел погрешности, в пределах которого координаты частицы могут быть измерены одновременно с соответствующей компонентой импульса вдоль той же оси. В квантовой механике неопределенность в измерении координат частицы Math \ Delta X/Math и соответствующей компоненты Math \ Delta P_X/Math не может быть нулевой в одно и то же время.
Math \ delta p_x \ delta x \ ge \ hbar/Math.
Для одной частицы с нулевым электрическим зарядом и спином, если оператор Math ⌘ wide-hat relief<\mathbf
>/Математика определяется следующим образом
Поскольку результаты дифференцирования по двум независимым переменным не зависят от порядка дифференцирования, операторы трех компонент импульса являются соответствующими.
Видно, что все три компонента импульса могут иметь точные значения одновременно.
Сингулярности и собственные значения операторов импульса являются решениями уравнения.
править Терминологические нюансы
В англоязычной традиции импульс называется «momentum», а английское «impulse» соответствует математическому варианту\ delta \ mathbf
/ математика.
- ↑ Aydin Sayili (1987). «Ibn Sīnā and Buridan on the Motion of the Projectile». Annals of the New York Academy of Sciences 500 (1): 477–482. DOI:10.1111/j.1749-6632.1987.tb37219.x. “Thus he considered impetus as proportional to weight times velocity. In other words, his conception of impetus comes very close to the concept of momentum of Newtonian mechanics.”
Персональные инструменты
Пространства имён
Варианты
Просмотры
Действия
Поиск
Навигация
Инструменты
- Последнее изменение этой страницы: 10:32, 11 сентября 2018.
- К этой странице обращались 3426 раз.
Эта страница доступна на условиях Свободной документации GNU. Материал может быть скопирован, если в тексте статьи (на той же странице) содержится активная ссылка на источник копирования. В некоторых случаях могут применяться условия Creative Commons Attribution-Sharealike (CC BY-SA 3.0). Для получения дополнительной информации см. страницу обсуждения и историю обработки. В частности, на записи, размещенные в Википедии, распространяется CC by-sa 3.0. Отчеты о переводах всегда доступны на страницах История и Обсуждение.
В тексте упоминаются организации, признанные на территории Российской Федерации террористическими и/или в отношении которых вынесены судебные решения, которые могут быть законно исполнены для запрета их деятельности. К ним относятся:.
Признанные террористические организации: «Исламское государство» (другие названия: «Исламское государство Ирака и Сирии», «Исламское государство Ирака и Леванта», «Исламское государство Ирака и Сама»), «Объединенное кавказское высшее военное подразделение моджахедов «Маджлисуль Шура», «Иксекия и Народное собрание Дагестана», «База» («Аль-Каида»), «Братья-мусульмане» («Эмиры Кавказа»), «Джебхат ан-Нусра» К. Минин, Д. Аум Синрикё (Аум, Алеф) — см. полный список.
Деятельность, запрещенная судебными решениями: межгосударственные большевистские общественные организации, движение против нелегальной иммиграции, украинская организация «Правый сектор», украинская организация «Украинская национальная ассамблея — Украинская народная самооборона имени Стефана Бандеры». Украинская организация «Тризуб имени Степана Бандеры», украинская организация «Братство», региональная общественная коалиция — «Народная социальная инициатива» (другие названия: «Народная социальная инициатива», «Национал-социалисты»), региональная общественная коалиция «Национальный политический союз». Русские», Общероссийская политическая партия «Воля», общественное объединение «Народ крымских татар», религиозная организация «Центр управления религиозными организациями Свидетелей Иеговы в России» и ее местная религиозная организация — общественное движение «АртПодготовка» — см. полный список.
Работа силы — это мера действия силы, в соответствии с ее измерением и адресом, а также перемещение точки приложения силы. Для постоянной мощности и прямолинейного сдвига проект определяется уравнением
ИНФОФИЗ
Дети часто не верят, что они могут учиться и учиться, и считают, что учиться очень трудно.
Все тела с массой и скоростью также обладают импульсом. Импульс тела направлен в ту же сторону, что и скорость тела.
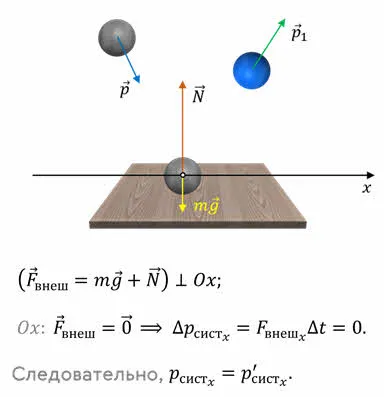
Импульс объекта — это векторная величина.
Единицей СИ импульса является килограмм-метр/секунда кг-м/с.
Законы и формулы
Мы используем файлы cookie, хранящиеся на вашем компьютере, для улучшения работы нашего сайта и удобства пользователей. Нажимая кнопку «Принять», вы информируетесь об использовании файлов cookie на нашем сайте и подтверждаете свое согласие с их использованием. Вы можете отключить файлы cookie в настройках своего браузера.
У нас 89 гостей и нет других зарегистрированных пользователей.
Если вы являетесь автором или владельцем авторских прав на материал и возражаете против его использования на моем сайте, пожалуйста, свяжитесь со мной. Информация будет удалена в кратчайшие сроки.
Спасибо автору и правообладателю за согласие разместить материал на моем сайте! Вы вносите неоценимый вклад в воспитание, обучение и развитие нового поколения.
©2022. ДудкоЕлена| Infofiz.ru 2011-2021 | Все права защищены| Все права защищены. Дудко Елена |Все материалы взяты из открытых источников и могут быть просмотрены только на локальном компьютере в целях импорта. Все права на статью, книгу, видео- и аудиоматериалы принадлежат автору и издателю. Любое распространение и/или коммерческое использование не допускается без разрешения законного владельца.