Если два участка ограничивают кривую одного размера, то эти оси равны друг другу. Из этого правила вытекает следующая закономерность.
Решение для разгрузки дорог. Что такое хорды и нужны ли они московскому региону
Струны продолжают строить в Москве. Эти дороги предназначены для ускорения движения транспорта и соединения районов более удобным способом. Струны помогают жителям как в столице, так и в пригородах.
Общая протяженность дорог Москвы составляет 3,6 тыс. км, но дорожная сеть столицы в два-три раза меньше, чем в других крупных городах мира. Другими словами, дороги занимают всего 8% территории города, в то время как европейская норма составляет 15-20%.
Строительство струн называют одним из главных проектов дорожного строительства на ближайшие три года. Эти дороги готовы на 72%.
В Москве полностью построена только одна нитка — северо-западная. Она соединяет три столицы на севере, северо-западе и западе. Общая протяженность этой дороги составляет 83 км. Три части — северо-восточная, юго-восточная нитка и южный Локард — были частично построены. Например, северо-восточная часть идет от МКАД на север до Большой Академической, затем дорога прерывается и вновь появляется у Северо-Восточного управления, выходя на МКАД с другой стороны — в районе Лязанского проспекта. Эта и другие струны будут завершены в 2021-2023 годах.
Результаты существующей хордовой сети
За 10 лет, благодаря этим дорогам, водители сократили трафик на 20%, так как время в пути от спальных районов до центра сократилось на 10 минут. По мнению московских экспертов, эти нитки станут четвертым транспортным кольцом, соединенным с МКАД.
Благодаря строительству дороги стало на 35% больше привлекательных точек притяжения. Кроме того, время прибытия аварийных служб сократится на 20%, а маршруты из центра на МКАД в часы пик сократятся на 20%.
Количество автомобилей на существующих автомагистралях также будет сокращено. Например, пробки на МКАД уменьшатся на шесть баллов вместо восьми, на Кутузовском проспекте — на единицу, на Сиртском кольце (ТТК) и Ярославском шоссе — на единицу.
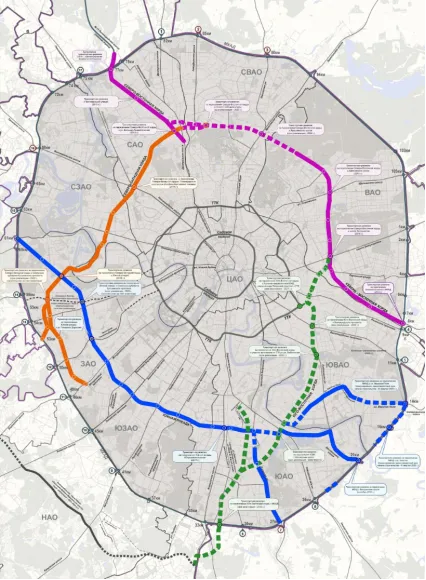
Северо-восточные (фиолетовые), северо-западные (оранжевые), юго-восточные (зеленые) и южные (синие) струны. Серая линия — Московская кольцевая автодорога.
Строительство северо-западной нитки снизило транспортную нагрузку на Главную улицу, ТТК, МКАД и прилегающие участки вылетной магистрали. Пробег автомобиля сократился на 10% при поездках через соседние районы.
Северо-восточный обход полезен тем, что он перемещает все транспортные средства на северо-восток от Москвы. После полного завершения строительства он уступит более 70 км дороги и снизит интенсивность движения в городе на 40 000 автомобилей в час.
Южная кольцевая автодорога отвечает за соединение основных магистралей. МКАД, Кутузовский проспект, Мишлинский проспект, проспект Варнадского, Ленинский проспект, Большую Южную улицу, проспект Болшавское шоссе, Каширский проспект и Рубин. Новая автомагистраль является предварительным решением для Московской кольцевой автодороги и Третьего транспортного кольца (ТТК), снижая транспортную перегрузку и доступ к М-9 «Балтия» и М-5 «Урал».
Юго-восточная нитка — это дорога, которая будет построена в 2024 году и только начала достраиваться: она объединяет 22 района, улучшает условия движения между шоссе Энтузиастов и Варшавским шоссе и соединяет основные магистрали: третье транспортное кольцо (ТТК), Рязанский и Волгоградский, а также многие дороги.
Москва вздохнула
Председатель Межрегионального общественного движения за права пешеходов «Коалиция пешеходов» Владимир Соколов в беседе с «360» отметил, что струны — одно из самых распространенных решений для разгрузки пробок на дорогах. Но, опять же, есть и недостатки. Чем свободнее дороги, тем больше людей хотят водить машину. В то же время их недостаточно, чтобы вызвать заторы.
Движение по кругу или диаметру сокращает расстояние вдвое. Если вы можете пересечь город по диаметру, вы можете сэкономить до 30 километров. Это бензин, экология — воздействие положительное. Скорость более экономична, и автомобиль преодолевает меньшие расстояния. Это также экономит личное время.
На струне происходит меньше несчастных случаев, но вероятность случайной смерти выше. Поскольку скорость движения на улицах выше, это означает, что транспортные средства также пользуются этой возможностью. Другими словами, если происходит авария, то, по словам Соколова, вероятность смерти водителя выше. Эта проблема частично решается с помощью таких дорожных разделительных ограждений. Это означает, что невозможно попасть в противоположный транспортный поток. Они также хорошо освещены и имеют качественные пешеходные дорожки.
Касательная линия — это линия, касательная к окружности в одной точке. Затем они перпендикулярны радиусу круга, когда радиус круга притягивается к нему. Вторичные линии — это линии, проходящие через две точки окружности. При взаимодействии этих линий можно наблюдать определенные закономерности.
Что такое хорда
Сердце человека состоит из четырех желудочков, через которые регулярно течет кровь: два желудочка и два предсердия. Поток крови проходит через клапаны, которые открываются по струнам. Когда на клапан подается напряжение, лопасти открываются, а когда напряжение ослабевает, лопасти закрываются. Это гарантирует, что кровь течет только в определенном направлении и не движется в обратном направлении.
Клапан натягивается специальными продольными нитями, называемыми струнами. Однако в дополнение к основному шнуру часто встречаются дополнительные шнуры. Они связаны с определенными частями сердца, но не участвуют в перекачивании крови. Поэтому их также называют псевдострунами.
Почему появляются ложные хорды сердца
В детском сердце легко найти ложные струны. Это делает педиатр через прокол грудной клетки (шумы в сердце). Обычно дополнительные струны образуются во время эмбрионального развития. Основными причинами являются
Наследственность — например, у родителей или бабушек и дедушек также было диагностировано это заболевание.
Неправильный образ жизни матери, особенно во время беременности (курение, употребление алкоголя, бесконтрольное употребление лекарств, токсических веществ), наличие хронических или инфекционных заболеваний.
Генетические факторы — мутации генов или хромосом.
Несбалансированное питание — слишком много животных жиров.
Тяжелая работа во время беременности.
Нездоровые условия окружающей среды.
Постоянный сильный стресс.
Ухудшение иммунной системы по различным причинам.
Дополнительная хорда: симптомы
Люди могут всю жизнь комфортно жить с дополнительными струнами, даже не подозревая об их существовании. В большинстве случаев они не вызывают никаких ощущений. Иногда, однако, пациенты могут заметить такие симптомы, как
Перемежающаяся усталость,.
Учащенное сердцебиение (тахикардия), особенно при волнении или столкновениях.
Вышеперечисленные симптомы не обязательно указывают на наличие струны, так как они могут быть связаны с другими причинами. Поэтому для определения точной причины необходимо провести профессиональную диагностику.
Шумский отметил, что струнные инструменты имеют наименьшее количество жертв. Пешеходных переходов мало, но есть многоуровневые пересечения с другими дорогами.
Свойства хорды и центрального угла
- Если хорды стягивают равные центральные углы, то эти хорды равны.
- Если хорды равны, то эти хорды стягивают равные центральные углы.
- Большая хорда стягивает больший центральный угол, меньшая хорда стягивает меньший центральный угол.
- Больший центральный угол стягивается большей хордой, меньший центральный угол стягивается меньшей хордой.
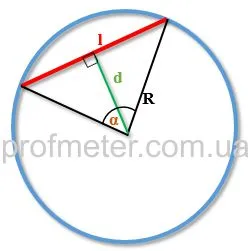
Символы в формуле: l — длина струны α — величина центрального угла R — радиус окружности d — длина перпендикуляра к центру окружности на струне
Длина периферийной струны равна удвоенной окружности, умноженной на половину полутона центрального угла. Сумма квадрата половины длины струны и квадрата перпендикуляра к этой струне равна квадрату радиуса окружности. Это уравнение вытекает из теоремы Пифагора.
Решение задач
ПРИМЕЧАНИЯ Если вы не можете найти решение своей проблемы, пожалуйста, опубликуйте его на форуме. Может быть добавлен урок геометрии. Проблема.
| Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ. |
Учитывая соотношение AS:SB = 2:3, пусть длина AS = 2x, SB = 3x.
Согласно свойствам строки ASxSB = CS x SD, мы имеем.
2x * 3x = 5 * 12 6x 2 = 60 x 2 = 10x = √10
Таким образом, AB = AS + SBAB = 2√10 + 3√10 = 5√10
| Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника. |
Решение. Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг). Поскольку градусная мера окружности равна 360 градусам, то
3,5x + 5,5x + 3x = 360 12x = 360 x = 30
Поэтому угловые значения центральных углов равны: 3 * 30 = 90 3,5 * 30 = 105 5,5 * 30 = 165
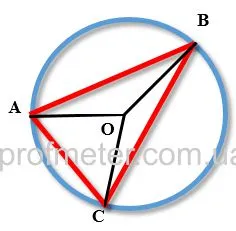
Угол образованного треугольника — это угол, вписанный в окружность. Обведенный угол равен 0,5 метра угла дуги, на которой он расположен. Таким образом, угол треугольника равен
90/2 = 45 105/2 = 52.5 165/2 = 82.5
ОТВЕТ: Каково значение угла треугольника, равного 45? 52.5; 82.5,.
ПРИМЕЧАНИЯ Если вы не можете найти решение своей проблемы, пожалуйста, опубликуйте его на форуме. Может быть добавлен урок геометрии. Проблема.
Решение задач
При решении задач, связанных с окружностями, струна часто служит основным элементом, который позволяет найти другие неизвестные. Во всех остальных задачах даны два параметра для нахождения третьего неизвестного. В круговых задачах струна является важным элементом.

- Найти высоту детали, которая была получена путем сгибания заготовки в дугу. В начальных данных обязательно присутствует хорда и длина дуги.
- Дана развертка, нужно найти длину части кольца. Задается хорда и диаметр.
- Также можно находить длину хорды. В случае если заданы уравнения прямой и окружности, которые пересекаются.
Полезно использовать схемы для решения задач на сечения внутри круга. Они оформлены линейкой и компасом, что делает принципы решения задач более понятными.
Если возникает ситуация, когда касательная и вторичная линии пересекаются, то и в этом случае может возникнуть закономерность. Теорема рассматривается для доказательства того, что AB 2 = AD*AC.
Хорда и радиус
Между этими понятиями существует следующая взаимосвязь.

- Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
- Существует также обратная зависимость — радиус, который перпендикулярен оси, делит её на две одинаковые составные части.
- Если ось не выступает диаметром этого круга, и радиус делит её пополам, то этот же радиус делит пополам и дугу, которая стягивается.
- Радиус, который делит пополам дугу, также делит и отрезок, который эту дугу стягивает.
- Если радиус является перпендикулярным стягивающей линии, то он делит пополам часть кривой, которую она ограничивает.
- Если радиус окружности разделяет на две идентичные части дугу, то он является перпендикулярным линии, которая эту дугу стягивает.
Отношения со вписанными углами
Угол, вписанный в окружность, подчиняется следующему правилу
- Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
- Если два вписанных в круг угла опираются на одну и ту же линию, но их вершины расположены по разные стороны этой прямой, то сумма таких углов будет равняться 180 градусам.
- Если два угла — центральный и вписанный — опираются на единую линию, и их вершины располагаются по одну сторону от неё, то величина вписанного угла будет равняться половине центрального.
- Вписанный угол, который опирается на диаметр круга, является прямым.
- Равные между собой по размеру отрезки стягивают равные центральные углы.
- Чем больше величина стягивающего отрезка, тем больше величина центрального угла, который она стягивает. И наоборот, меньшая по размеру линия стягивает меньший центральный угол.
- Чем больше центральный угол, тем больше величина отрезка прямой, который его стягивает.
Взаимодействия с дугой
Если два участка ограничивают кривую одного размера, то эти оси равны друг другу. Из этого правила вытекает следующая закономерность.
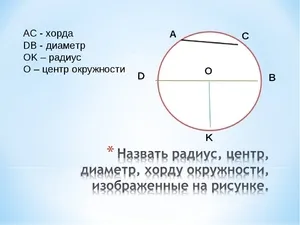
- Две равные между собой хорды стягивают равные дуги.
- Если рассматривать две дуги, размер которых меньше половины окружности, то чем больше дуга, тем больше хорда, которая будет её стягивать. Напротив, меньшая дуга будет стягиваться меньшей по величине хордой.
- Если же дуга превышает половину окружности, то здесь присутствует обратная закономерность: чем меньше дуга, тем больше хорда, которая её стягивает. И чем больше дуга, тем меньше ограничивающая её хорда.
Нить, которая сужает ровно половину круга, является его диаметром. Если две прямые окружности параллельны друг другу, то дуга, заключенная в этих отрезках, также равна. Однако не путайте замкнутую дугу с дугой, заключенной в те же линии.
ОТВЕТ: высказывания очень похожи — если закрыть картинку и слово, то они абсолютно одинаковые — здорово, правда? Это сходство также выглядит гораздо лучше, когда утверждения находятся рядом друг с другом.
Касательная и секущая
Есть две теоремы о касательных, исходящих из одной точки. Он говорит, что если через точку O провести две прямые OK и ON, то они будут равны друг другу. Перейдем к доказательству теоремы.
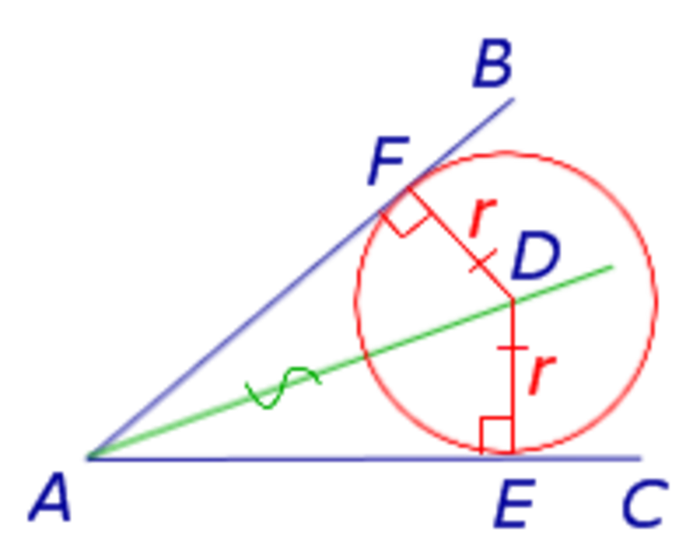
Рассмотрим два правильных треугольника AFD и AED. Так как катеты DF и DE равны радиусу окружности, а AD является общей гипотенузой, то эти треугольники равны между собой и подписываются равенством треугольников. Это дает AF = AE.
Если возникает ситуация, когда касательная и квадратичная линии пересекаются, в этом случае также можно извлечь закономерность. Проверьте теорему и докажите, что AB 2 = AD*AC.
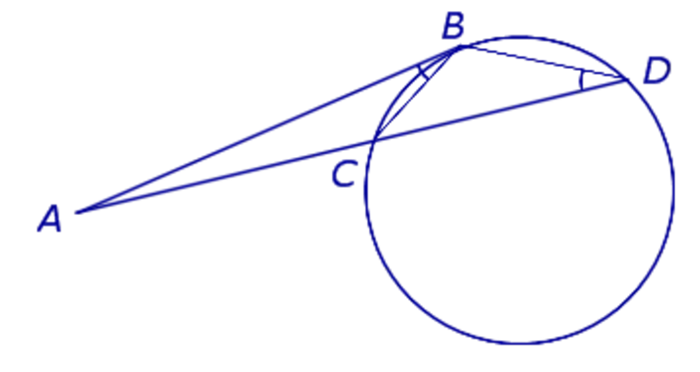
Предположим, что у нас есть касательная прямая AB и квадратичная AD, начинающиеся из одной и той же точки A. Обратите внимание на угол ABC. Это соответствует дуге BC и, по свойствам окружных углов, ее значение составляет 0,5 градуса от измеренного значения дуги. Она находится над ним. Как свойство окружного угла, значение угла BDC также равно половине дуги BC. Треугольники ABD и ABC являются линейными, так как угол A является общим, а угол ABC равен углу BDC. Исходя из теории, можно получить соотношение AB / CA = DA / AB, а переписав это соотношение в соответствующей форме, можно получить уравнение AB 2 = AD*AC. Это нужно было доказать.
Подобно тому, как существуют две теоремы о касательных, существуют две теоремы о малых касательных. Эта теорема проста, как и любая другая теорема. Поэтому рассмотрите доказательство и увидите, что AB * AC = AE*AD.
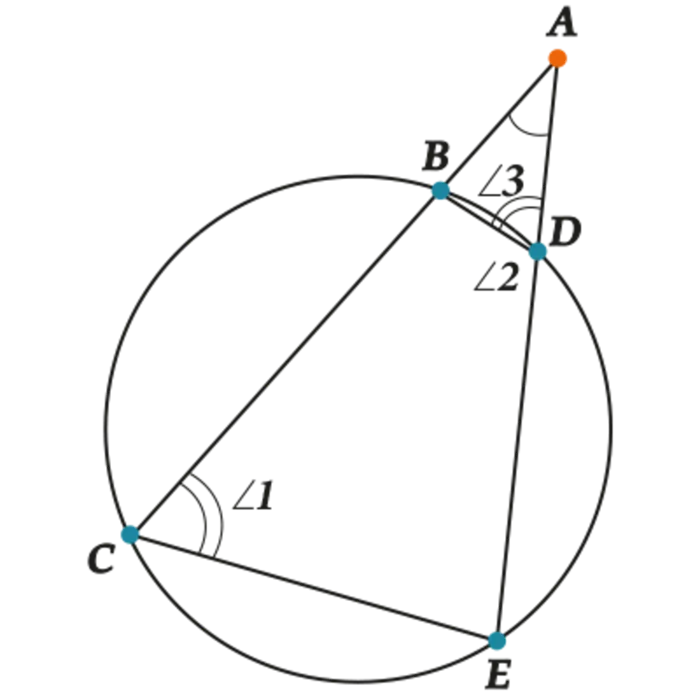
Проведите две прямые через точку A, чтобы получить две прямые AC и AE. Проведите две нити, соединяющие точки C и B и B и D. Получите два треугольника ABD и CEA. Обратите внимание на вписанный четырехугольник BDCE. Учитывая свойства вписанной окружности четырехугольника, сумма углов BDE и ECB равна 180 градусам. Тогда, согласно свойствам смежных углов, сумма значений углов BDA и BDE также равна 180.
Отсюда можно получить два уравнения, из которых следует, что углы ECB и BDA равны: BDA + BDE = 180; BDE + ECB = 180. Мы можем записать все это в виде одновременного уравнения и вычесть первое уравнение из второго, чтобы получить результат ΕΚΤ = BDA.
Возвращаясь к треугольникам ABD и CEA, можно сказать, что они подобны, так как угол A является общим, а углы ECA и BDA равны. Теперь мы можем записать соотношение сторон как: AB / AE = AD/AC; поэтому AB * AC = AE*AD.
Решение задач
При решении задач, связанных с окружностями, струна часто служит основным элементом, который позволяет найти другие неизвестные. Во всех остальных задачах даны два параметра для нахождения третьего неизвестного. В круговых задачах струна является важным элементом.

- Найти высоту детали, которая была получена путем сгибания заготовки в дугу. В начальных данных обязательно присутствует хорда и длина дуги.
- Дана развертка, нужно найти длину части кольца. Задается хорда и диаметр.
- Также можно находить длину хорды. В случае если заданы уравнения прямой и окружности, которые пересекаются.
Полезно использовать схемы для решения задач на сечения внутри круга. Они оформлены линейкой и компасом, что делает принципы решения задач более понятными.








