Проекции в картографии. Что такое картографическая проекция.

Если статья окажется интересной, я постараюсь написать продолжение о проекциях, используемых для представления отдельных стран или регионов, сосредоточившись, как и в этой статье, на основных свойствах этих проекций для визуализации данных, инфографики и тому подобного.

Что такое картографическая проекция

Картографические проекции можно классифицировать двумя основными способами:

— В зависимости от типа искажений,

— По типу меридианов и параллелей обычной картографической сетки.

Картографическая сетка считается нормальной, если меридианы и параллели на карте в этой проекции представлены более простыми линиями, чем координатные линии любой другой сферической системы координат.

В зависимости от типа деформации проекции делятся на конформные, изогональные, промежуточные и произвольные.

Равноугольные (конформные) проекции — это такие проекции, в которых бесконечно малые элементы карты подобны соответствующим элементам глобуса. В этих проекциях бесконечно малый круг, взятый в любой точке земного шара, при переносе на карту также представляется бесконечно малым кругом, то есть отсутствие искажений в изогональных проекциях преобразуется в круг. В изогональных проекциях для бесконечно малых фигур на карте и на глобусе соответствующие углы равны, а стороны пропорциональны. Например, на рисунке 15a, b AMK, a T=n. Угол между меридианами и широтами на карте
= t = p = a = B, P = t2,

Равенство масштабов показывает, что масштаб в любой точке карты не зависит от направления в истинно угловых проекциях. Но

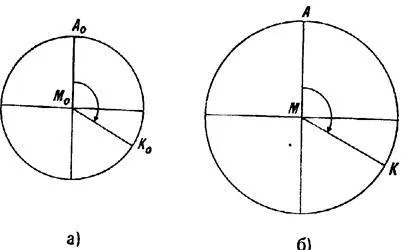
Рисунок 1. Бесконечно малый круг на глобусе и на карте в равнобедренной проекции.

Когда мы перемещаемся от точки к точке (когда мы меняем координаты точки), масштаб меняется. Это означает, что одни и те же маленькие бесконечно малые круги в разных точках Земли отображаются на карте как бесконечно малые круги, но с разными размерами (в данном случае бесконечно малым кругом на Земле можно считать круг диаметром около 1 см).

Равновеликие (эквивалентные) проекции — это такие проекции, в которых масштаб территории одинаков во всех точках карты. В этих проекциях круг бесконечно мал (рис. 2а),

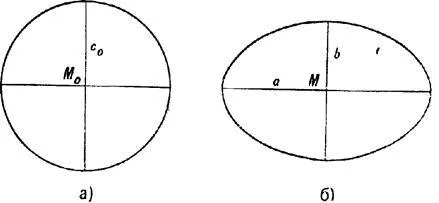
Рис. 2. Круг на глобусе и эллипс на карте в равновеликой проекции

представлен на карте бесконечно малым эллипсом с такой же площадью (рис. 2 b).

Поскольку площадь эллипса

и площадь круга по формуле

К этим прогнозам применимо следующее уравнение

На сайте

Таким образом, произведение масштабов по главным направлениям в изодинамических проекциях равно единице.

Если в проекциях на равные углы равенство углов сохраняется только в случае бесконечно малых фигур, то в проекциях на равные плоскости площади всех фигур сохраняются на карте независимо от их размера. В этих проекциях углы между меридианами и параллелями на карте не обязательно должны быть равны 90°. Следует помнить, что свойства равнонаправленности и изоаксиальности несовместимы в проекции, т.е. не может быть проекций, в которых одновременно сохраняется равенство углов и площадей во всех точках карты.

Эквивалентные промежуточные проекции — это проекции, в которых длины в одном из основных направлений сохраняются в каждой точке карты. Для этих проекций a =.

Иногда под промежуточными проекциями понимают также такие проекции, в которых отношение остается постоянным, хотя и не равно единице.

Конические проекции

Конические проекции — это проекции, в которых параллели нормальной сетки представлены дугами концентрических окружностей, а меридианы — их радиусами, причем углы между ними на карте пропорциональны соответствующим различиям в длине в реальности.

Геометрически картографическая сетка может быть получена в этих проекциях путем проецирования меридианов и параллелей на боковую поверхность конуса и последующего разворачивания этой поверхности в плоскость.

Представим себе конус, касательный к земному шару вдоль параллели AoBoCo (рис. 4). Продлим плоскости географических меридианов и параллелей на земном шаре до их пересечения с поверхностью конуса. Линии пересечения острых плоскостей с поверхностью конуса принимаются соответственно за изображения меридианов и параллелей на глобусе. Если пересечь поверхность конуса по его конфигурации и преобразовать ее в плоскость, то мы получим карту сетки на плоскости в одной из проекций конуса (рис. 5).

Параллели со сферы на поверхность конуса можно перенести и другим способом, а именно проецированием лучей, исходящих из центра сферы или из точки, лежащей на оси конуса, откладывая на проекции меридианы в обоих местах от параллели, касающейся совмещенных дуг меридианов сферы, проведенных между параллелями, и проводя через точки размещения концентрические окружности из точки S (рис. 5), как из центра. В последнем случае параллели имеют такое же расстояние на плоскости, как и на глобусе.

Описанными выше способами переноса географической сетки с глобуса на поверхность конуса, параллели на плоскости являются

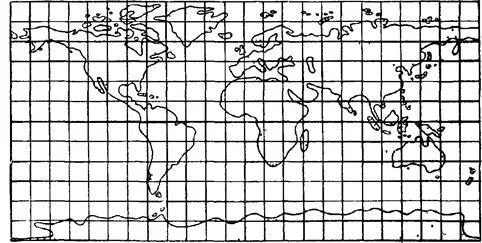
Рис.4 Конус, касающийся земного шара параллелью.

Рис. 5 Осаждение концентрических кругов.

Сетка карты в конической проекции представлена дугами концентрических окружностей, а меридианы — прямыми линиями, начинающимися из точки и образующими между собой углы, пропорциональные соответствующим разницам в длине.

Последняя зависимость может быть выражена следующим уравнением.

Где

— коэффициент, называемый экспонентой конической проекции. Для конических проекций он всегда меньше единицы.

Радиусы этих параллелей, т.е.

Таким образом, сетка изображений может быть построена непосредственно в плоскости, минуя проекцию на вспомогательную поверхность конуса, если экспонента и

При выборе конических проекций для заданной площади необходимо найти такое значение α и такое соотношение между p и cp, чтобы получить проекцию (равностороннюю, равнобедренную, изометрическую или произвольную) с минимально возможным искажением.

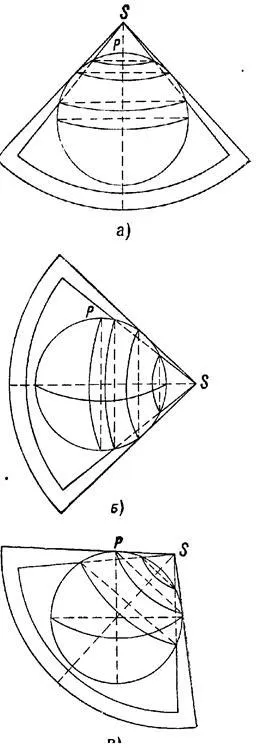
Конус может быть расположен по-разному по отношению к глобусу. Ось конуса может совпадать с полярной осью сферы ПП, образовывать с ней угол 90° и, наконец, пересекать ее под любым углом. В первом случае конические проекции называются нормальными (прямыми), во втором — поперечными, в третьем — косыми. На рис. 7 показано положение конусов в нормальной (a), поперечной (b) и косой (c) конических проекциях. Каждый из этих конусов может в свою очередь находиться в касательном или вторичном конусе.

Цилиндрические проекции

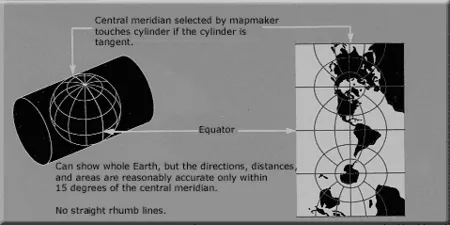
Цилиндрические проекции — это проекции, в которых параллели нормальной сетки представлены параллельными прямыми, а меридианы — изометрическими прямыми, перпендикулярными параллельным прямым.

С геометрической точки зрения картографическая сетка в этих проекциях может быть определена путем проецирования меридианов и параллелей земного шара на боковую поверхность цилиндра и последующего разворачивания этой поверхности в плоскость.

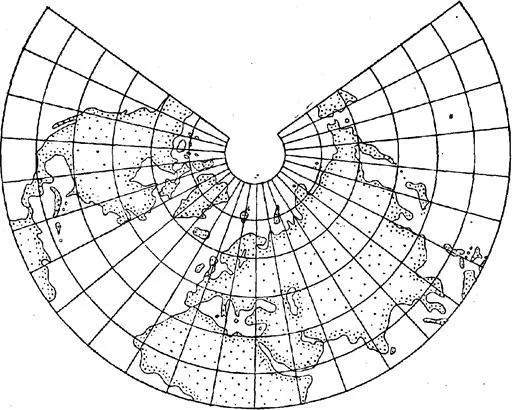
Рисунок 8. Картографическая сетка в конической проекции с равными интервалами.

Представим себе цилиндр, касающийся земного шара по экватору (рис. 9). Проведем плоскость географических меридианов и параллелей до точки пересечения с боковой поверхностью цилиндра. В качестве изображений меридианов и параллелей на поверхности цилиндра мы рассмотрим линии пересечения этих плоскостей с поверхностью цилиндра. Разрежьте поверхность цилиндра по линии фигуры и разверните его в плоскость. Затем на этой плоскости изображается картографическая сетка в одной из цилиндрических проекций, а также в конических проекциях. Параллели в регулярной картографической сетке могут быть перенесены на поверхность цилиндра другими способами, а именно: Проекцией с лучами, исходящими из центра сферы или из точки на оси цилиндра, путем размещения на меридианах проекции по обе стороны от экватора выровненных дуг меридианов сферы, соединенных между параллелями, и последующего проведения их через точки прикрепления прямых, которые параллельны. В последнем случае параллели на карте равноудалены.

Рассматриваемая цилиндрическая проекция (рис. 9) — это проекция на тангенциальный цилиндр. Таким же образом можно построить проекцию на тангенциальный цилиндр.

На рисунке 10 показан цилиндр, пересекающий земной шар по параллелям AFB и CKD. Очевидно, что в первом случае на экваторе (рис. 9) и во втором случае на параллели пересечения AFB и CKD (рис. 10) масштаб на карте равен первичному масштабу, т.е. экватору.

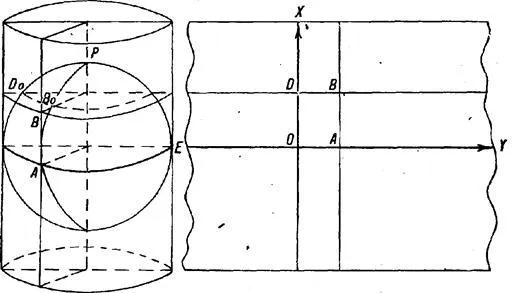
Рисунок 9. Цилиндр, касательный к земному шару вдоль экватора, и часть поверхности цилиндра, развернутая на плоскости, причем указанные параллельные точки пересечения сохраняют свою долготу на карте. Цилиндр может быть расположен по-разному по отношению к глобусу.

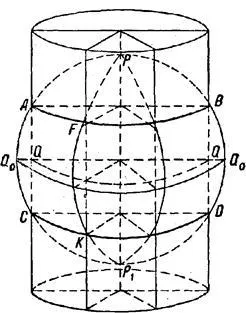
Рисунок 10. Цилиндр пересекает земной шар вдоль широт.

В зависимости от положения оси цилиндра по отношению к оси шара цилиндрические проекции могут быть регулярными, поперечными и косыми, как и конические проекции. Соответственно, картографическая сетка в этих проекциях называется регулярной, поперечной и косой. Поперечные и косые картографические сетки в цилиндрических проекциях имеют вид сложных кривых линий.

Как и в случае с коническими проекциями, для построения регулярных сеток цилиндрических проекций не требуется сначала проецировать поверхность сферы в цилиндр, а затем складывать его в плоскость. Для этого достаточно знать ортогональные координаты x и y пересечения параллелей и меридианов на плоскости. Для цилиндрических проекций дистальная ось x представляет собой расстояние параллелей от экватора, а дистальная ось y — расстояние меридианов от центрального (осевого) меридиана.

Как сделать точную карту?

При создании карты невозможно полностью избежать искажений. Однако можно устранить любой вид искажений. В так называемых изоаксиальных проекциях поверхности сохраняются, но углы и формы искажаются. Равноугольные проекции полезны для экономических, территориальных и других мелкомасштабных тематических карт, например, для расчета площади загрязненных территорий или для лесного хозяйства. Примером такой проекции является коническая равноугольная проекция Альберса, которая была разработана немецким картографом Генрихом Альберсом в 1805 году.

Изогональные проекции — это проекции без угловых искажений. Эти проекции полезны для целей навигации. Угол на земле всегда равен углу на такой карте, а прямая линия на земле представлена прямой линией на карте. Это позволяет штурманам и путешественникам планировать маршрут и точно следовать ему, используя показания компаса. Однако линейный масштаб карты в этом представлении зависит от положения точки на карте.

Самой старой изографической проекцией считается стереографическая проекция, которую изобрел Аполлоний Пергский около 200 года до нашей эры. Эта проекция до сих пор используется для карт звездного неба, в фотографии для сферических панорам и в кристаллографии для представления точечных групп кристаллической симметрии. Однако использование этой проекции в навигации будет затруднено из-за чрезмерного линейного искажения.

Проекция Меркатора

В 1569 году фламандский географ Герхард Меркатор (латинское имя Герард Кремер) разработал изогональную цилиндрическую проекцию, которая позже была названа его именем и стала одной из самых важных и широко используемых картографических проекций, и впервые использовал ее в своем Атласе (полное название: «Atlas oder Kosmographische Betrachtungen über die Erschaffung der Welt und die Ansicht der Schöpfung»).

Для построения цилиндрической проекции Меркатора геоид Земли помещается в цилиндр таким образом, чтобы геоид был направлен по касательной к цилиндру вдоль экватора. Проекция осуществляется путем проведения лучей из центра геоида в точку пересечения с поверхностью цилиндра. Если затем разрезать цилиндр вдоль оси и развернуть его, то получится плоская карта поверхности Земли. Вы можете думать об этом так: Сфера оборачивается вокруг экватора листом бумаги, в центр сферы помещается лампа, и на листе бумаги появляются изображения континентов, островов, рек и т.д., проецируемые лампой. Если бы бумага имела просветляющий слой, то при разворачивании листа получилась бы карта.

В такой проекции полюса находятся на бесконечном расстоянии от экватора и поэтому не могут быть показаны на карте. На практике карта показывает верхние и нижние широты примерно до 80° северной широты и южной широты.

Параллели и меридианы картографической сетки изображаются на карте параллельными прямыми линиями и всегда вертикальны. Расстояния между меридианами одинаковы, а расстояние между параллелями такое же, как расстояние между меридианами вблизи экватора, но быстро увеличивается к полюсам.

В этой проекции масштаб не является постоянным, а увеличивается от экватора к полюсам с обратным косинусом широты, но вертикальный и горизонтальный масштабы всегда одинаковы.

Равенство вертикального и горизонтального масштабов обеспечивает изогональность проекции — угол между двумя линиями на местности равен углу между изображениями этих линий на карте. Это дает хорошее представление о форме небольших объектов. Однако искажение поверхности увеличивается по направлению к полярным областям. Например, хотя Гренландия всего на одну восьмую меньше Южной Америки, в проекции Меркатора она кажется больше. Большие деформации области делают проекцию Меркатора непригодной для общегеографических карт мира.

Линия, проведенная между двумя точками на карте в таком виде, пересекает меридианы под одинаковым углом. Эта линия называется ромбом или ромбовидной линией. Следует отметить, что эта линия не описывает кратчайшее расстояние между точками, но всегда показывается как прямая линия в представлении Меркатора. Это делает проекцию идеальной для целей навигации. Например, если мореплаватель хотел проплыть из Испании в Вест-Индию, ему достаточно было провести линию между этими двумя точками, и он знал, в каком направлении по компасу нужно двигаться в любой момент времени, чтобы достичь пункта назначения.

С точностью до сантиметра

Для использования проекции Меркатора (как и любой другой проекции) необходимо установить систему координат на поверхности Земли и правильно выбрать так называемый опорный эллипсоид — эллипсоид вращения, который приближенно повторяет форму поверхности Земли (геоид). Для местных карт в России в качестве такого опорного эллипсоида с 1946 года используется эллипсоид Красовского. В большинстве европейских стран используется эллипсоид Бесселя. Наиболее распространенным эллипсоидом для глобального картографирования сегодня является Всемирная геодезическая система 1984, WGS-84, которая определяет трехмерную систему координат для определения местоположения позиций на поверхности Земли относительно центра масс Земли с отклонением менее 2 см. Для соответствующего эллипсоида применяется классическая изогональная цилиндрическая проекция Меркатора. Сервис Яндекс.Карты, например, использует эллиптическую проекцию Меркатора WGS-84.

В последнее время, в связи с быстрым ростом картографических веб-сервисов, стал популярен другой вариант проекции Меркатора, основанный на сфере, а не на эллипсоиде. Такой выбор обусловлен более простыми расчетами, которые могут быть быстро выполнены непосредственно в браузере клиентами этих сервисов. Эту проекцию часто называют «сферическим Меркатором». Этот вариант представления Меркатора используется как в Google Maps, так и в 2ГИС.

Более известным вариантом проекции Меркатора является изогональная проекция Гаусса-Крюгера. Он был введен выдающимся немецким ученым Карлом Фридрихом Гауссом в 1820-1830 годах для составления карты Германии — так называемого Ганноверского треугольника. В 1912 и 1919 годах ее разрабатывал немецкий геодезист Л. Крюгер.

По сути, это цилиндрическая поперечная проекция. Поверхность земного эллипсоида разделена на зоны в три или шесть градусов, ограниченные меридианами от полюса к полюсу. Цилиндр касается центрального меридиана зоны и проецируется на этот цилиндр. Всего можно определить 60 шестиградусных полос или 120 трехградусных полос.

В России для топографических карт масштаба 1 : 1000000 используются шестнадцатеричные зоны. Трехградусные зоны используются для топографических карт масштабов 1 : 5000 и 1 : 2000, где продольные меридианы совпадают с осевыми и граничными меридианами шестиградусных зон. При съемке городов и территорий для строительства крупных инженерных сооружений можно использовать частные зоны с осевым меридианом в центре объекта.

‍ Картографические проекции

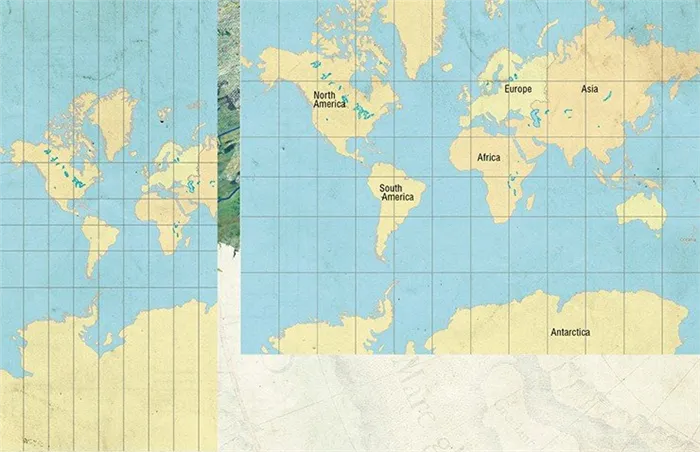
География, буквально «описание земли», начинается с визуального представления. Наиболее популярным методом является географическая карта. Но взгляд на карту может удивить и сбить с толку. Например, Гренландия на некоторых картах занимает больше места, чем вся Южная Америка, хотя она в восемь раз меньше. Белый континент» Антарктида может выглядеть как почти круглая точка или как широкая полоса, занимающая всю нижнюю часть карты Земли. А изображения континентальной части России могут отличаться настолько, что на одних картах очертания Чукотки визуально находятся вровень с очертаниями полуострова Таймыр, а на других — выше или ниже. Таймыр — это, по сути, самая северная оконечность материковой части России — мыс Челюскин. Чтобы научиться «читать» географические карты, необходимо знать, как они создаются.

Форма Земли довольно сложна (ее называют геоидом), но она приблизительно представляет собой вращающийся эллипсоид с полуосями 6378 км и 6357 км: «несферическая» форма ее настольной копии будет миллиметровой. Лучшим «портретом» Земли является глобус: проекция земной поверхности на сферу. Физическая система координат на планете (и на Земле) сферическая, положение точки определяется двумя углами. Долгота относится к главному меридиану (Гринвич), а широта — к экватору. На глобусе эта система координат представлена сеткой — параллели и меридианы с фиксированным угловым шагом (обычно $10°$ — $20°$). Визуально привлекательный глобус также имеет некоторые непреодолимые недостатки: например, невозможно построить глобус, на котором изображено конкретное место или город. Правильное и целесообразное изображение земной поверхности на плоской карте является основной задачей картографии. Математическая задача состоит в том, чтобы найти изображение сферы (глобуса) на плоскости (карте) и вывести формулы, связывающие координаты точек на сфере и карте. Этой проблемой и тесно связанными с ней вопросами геодезии занимались многие великие математики, сочетавшие изучение оригинальной математической задачи с разработкой ценных практических инструментов. Леонгард Эйлер писал теоретические работы, рисовал и редактировал карты, руководил картографической работой в Академии наук и гордился своим вкладом в доведение российской географии «до ума». К. Ф. Гаусс не только открыл важную общую теорему, но и активно участвовал в измерениях геодезических полей. П. Л. Чебышев сформулировал теорему о «наиболее благоприятной» (в определенном смысле) проекции, которая дает практическое руководство картографам. Кажется, что окончательное оптимальное решение проблемы уже должно быть найдено. Однако в реальности невозможно создать точную карту с сохранением всех расстояний, поэтому в каждом слое карты возникают искажения. Это следует из теоремы Гаусса, которую он назвал «замечательной»: если одна поверхность отображается с сохранением расстояний до другой, то ее гауссовы кривизны совпадают в соответствующих точках. Гауссова кривизна — это числовая характеристика, которая предоставляет информацию о степени и характере кривизны поверхности в данной точке. А поскольку кривизна сферы везде положительна, в то время как кривизна плоскости равна нулю, невозможно изобразить сферу на плоскости с сохранением расстояний. С другой стороны, можно показать, что поверхность с нулевой кривизной можно «развернуть» в плоскости, сохраняя расстояния. Причина деформаций заключается в том, что при проецировании (изображении) сферы на плоскость расстояния между точками изменяются неравномерно. Степень удлинения или укорочения длины пути может также зависеть от положения точки на сфере, из которой выходят пути, и даже от направления, в котором они выходят из точки. Визуальное представление о деформациях можно получить, рассматривая изображения одних и тех же маленьких кругов на глобусе на карте. Эти изображения, называемые эллипсами деформации, показывают зависимость изменений одного и того же расстояния точек окружности от их центров и то, как эти изменения происходят в разных направлениях.

Разворот книги

Равноугольные проекции в любой точке сохраняют углы между проходящими через нее путями и масштабом во всех направлениях. А для страны, чье изображение на глобусе представляет собой единый непрерывный регион (т.е. граница состоит из одного «куска», это непрерывная кривая), такая проекция сохраняет дополнительные параметры. Знаменитая теорема Бернхарда Римана из комплексного анализа для конформных (угловых консервативных) представлений может быть переформулирована на картографическом языке: Для любой «единой сопредельной» страны изогональная проекция может быть настроена так, что плоская карта страны будет представлять собой круг, а ее столица — центром круга. Для тех, кто интересуется теорией функций комплексных переменных, здесь приведена полная формулировка теоремы Римана. Для любой нечетной связной области $G$ в расширенной комплексной плоскости $\overline.<\mathbb C>$, граница которой содержит более одной точки, мы находим конформное представление области $G$ в единичном круге $B_1(0)=$. Такое представление уникально, если мы выберем $z_0\in G$, $w_0\in B_1(0)$, $α\in 0, 2π)$ произвольно и зададим условия регуляризации: $f(z_0)=w_0$, $\arg f'(z_0)=α$.

Рассматривая цилиндрическую проекцию с той же скоростью, было установлено, что площадь сферической полосы, пересекаемой двумя параллельными плоскостями, равна площади соответствующей цилиндрической полосы. Это приводит к интересному наблюдению: площадь полосы на глобусе зависит только от расстояния между вторичными плоскостями, но не от близости полосы к экватору или полюсу. Интерпретация «съедобный»: Если круглый апельсин без кожуры разрезать на дольки одинаковой толщины, то площадь поверхности кожуры всех долек одинакова.

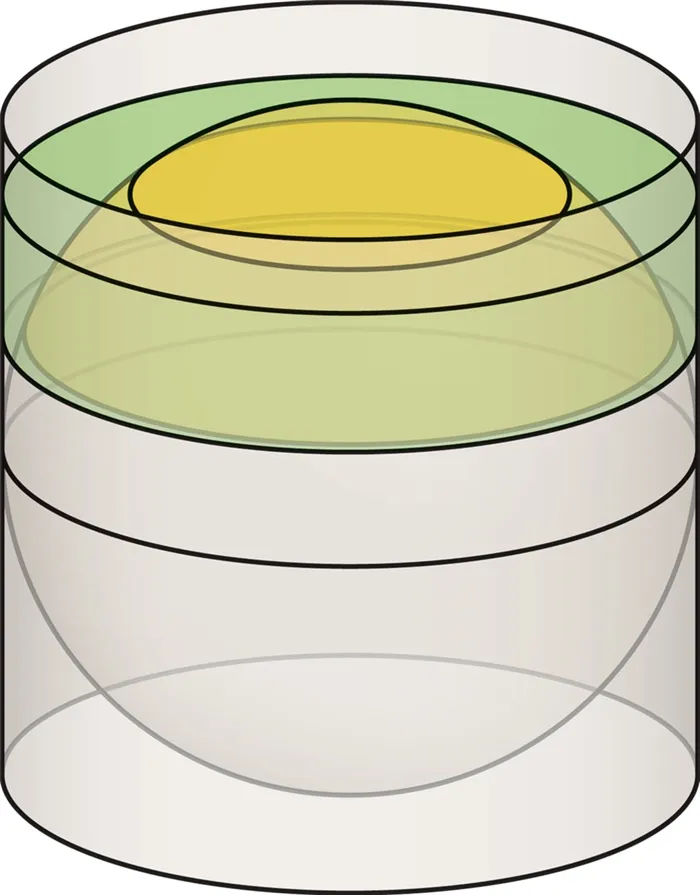
Концепция кривизны встречается в нескольких рассказах книги; геометрическое рассмотрение этой концепции является темой «Искривленных миров».

Слово «карта» лежит в основе термина «картография». Оно происходит из латинского языка (carta) и пришло туда из Греции как термин для обозначения папирусной бумаги. От этого корня происходят географические карты в немецком, русском и французском языках. В английском, испанском и итальянском языках используются слова map, mapa, mappa (также происходит от латинского, где mappa означает ткань или полотенце; слово пришло в латынь из финикийского языка). Разница в названиях связана с материалом, из которого изготавливаются карты в разных странах — бумага или ткань. Как ни странно, игральные карты во всех этих странах были сделаны из бумаги (card, karte, carte, carte, carte и т.д.).

Вы можете ознакомиться с результатами великих математиков в области картографии, просмотрев сборники их работ, изданные на русском языке. Леонард Эйлер «Избранные картографические труды» (М.: Изд-во Геодезической литературы, 1959); Карл Фридрих Гаусс «Избранные геодезические труды» (М.: Изд-во Геодезической литературы, 1957, 1958); Пафнутий Львович Чебышев «Полное собрание сочинений» (Тр. 5: Другие произведения. Биографические материалы. М.: Изд-во АН СССР, 1951); Пафнутий Львович Чебышев «Полное собрание сочинений» (Т. 5: Другие произведения. Биографические материалы. М.: Изд-во АН СССР, 1951).

Классификация

Основная классификация проекций, основанная на типе проекционной поверхности, на которую концептуально проецируется глобус. Проекции описываются контактом гигантской поверхности с землей с помощью неявной операции масштабирования. Эти поверхности могут быть цилиндрическими (например, Меркатора), коническими (например, Альберса) и плоскими (например, стереографическими). Однако многие математические прогнозы не подходят ни под один из трех методов концептуального проектирования. Поэтому в литературе можно найти примеры других равных категорий, таких как псевдоконические, псевдоазимутальные, ретроазимутальные и поликонические.

. Другой способ классификации проекций — по свойствам модели, которую они получают. Вот некоторые из наиболее распространенных категорий:

• Сохранение направления (азимутальное или зенитное), характеристики, возможная только от одной или двух точек до каждой другой точки
• Локальное сохранение (конформная или ортоморфный)
• Сохраняющая площадь (равновеликая, или эквиариальная, или эквивалентная, или аутентичная)
• Сохраняющая дистанция (эквидистантная), признак возможен только между одной или двумя точками и каждой другой точкой
• Сохранение кратчайшего маршрута, черта, сохраняемая только гномонической проекцией

Поскольку формальная проекция сферы не является развивающейся поверхностью, невозможно построить картографическую проекцию, которая была бы одновременно изоаксиальной и конформной.

Проекции по поверхности

Три эволюционирующие поверхности (плоскость, цилиндр, конус) представляют собой полезные модели для понимания, описания и эволюции картографических проекций. Однако эти модели имеют два важных ограничения. Во-первых, большинство используемых глобальных прогнозов не относятся ни к одной из этих категорий. С другой стороны, большинство проекций, относящихся к этим категориям, также не могут быть достигнуты естественным путем с помощью физических проекций. Как отмечает Л.П. Ли,

приведенные выше определения не относятся к цилиндрам, конусам или плоскостям. Проекции называют цилиндрическими или коническими, потому что они могут быть развернуты, образуя цилиндр или конус соответственно, но также лучше избегать изображения цилиндров и конусов, потому что они приводят ко многим недоразумениям. Это особенно верно для конических проекций с двумя стандартными параллелограммами: Их можно увидеть развернутыми в конусы, но это конусы, которые не просто соединены со сферой. Цилиндры и конусы — это удобные описания, но не более того.

Возражение Ли касается того, как абстрагируются термины цилиндрическая, коническая и плоскостная (азимутальная) в области картографических проекций. Если бы карты проецировались как свет, проходящий через земной шар на разворачивающуюся поверхность, то расстояние между параллелями соответствовало бы очень ограниченному числу возможностей. Такой цилиндрической проекцией (например) является:

1. имеет прямоугольную форму;
2. имеет прямые вертикальные меридианы, равномерно распределенные;
3. имеет прямые параллели, симметрично расположенные относительно экватора;
4. Имеет параллели, ограниченные тем местом, где они падают, когда свет падает через земной шар на цилиндр, с источником света где-то вдоль линии, образованной пересечением нулевого меридиана с экватором и центром сферы.

(Если повернуть глобус перед проецированием, параллели и меридианы не обязательно будут прямыми линиями. Вращения обычно не учитываются в классификации).

Место, где источник света светит вдоль линии, описанной в этом последнем условии, отвечает за различия между различными «естественными» цилиндрическими проекциями. Однако термин «цилиндрический», используемый в области картографических проекций, полностью снимает это последнее ограничение. Вместо этого параллели могут быть расположены в соответствии с алгоритмом, определенным разработчиком для нужд карты. Знаменитая проекция Меркатора — это проекция, в которой параллели не выводятся из проекции; вместо этого параллели устанавливаются по мере необходимости, чтобы удовлетворить свойству, согласно которому путь с фиксированной ориентацией всегда выглядит как прямая линия.

Цилиндрический

В проекции Меркатора ромбы выглядят как прямые линии. Румм — неподвижная опора. Пеленг — это направление движения компаса.

Обычная цилиндрическая проекция — это проекция, в которой меридианы нанесены на одни и те же вертикальные линии, а широты (параллели) — на горизонтальные линии.

Меридианы, соответствующие вертикальным линиям, можно представить, построив цилиндр, ось которого совпадает с осью вращения.

Немного экзотики и специальных случаев

Конечно, на этом разнообразие проекций не заканчивается. Было изобретено несколько. Некоторые просто выглядят странно (например, проекция Bonnet, где Земля представлена в виде фигуры, напоминающей нарезанное яблоко или стилизованное сердце), другие предназначены для конкретных ситуаций. Наверняка многие видели изображения карты мира, которая похожа на кожуру мандарина, снятую и сплющенную. Должно быть, это было так«Прерывистая проекция Гуде Гомолосика».Прерывистый просмотр Goode Homolosin WKID:54052 .

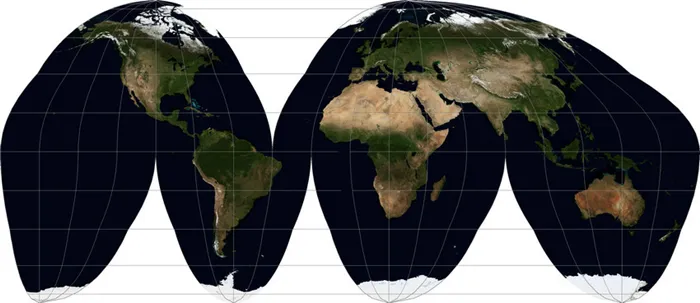
Его внешний вид соответствует своему названию. Его цель — представить размер (и в некоторой степени форму) объектов близко к их естественным пропорциям. Основная проблема, помимо названия и странного внешнего вида, заключается в том, что корректировка центрального меридиана не гарантирует, что большие участки земли не будут отрезаны. Что-то из списка пострадает: Гренландия, Исландия, Чукотка, Аляска. Лично я считаю, что проще наклеить картинки на отдельные страны, чем использовать такую карту, если только вы не хотите стилизовать свою работу под середину двадцатого века.

Есть некоторые проекции, которые по своей природе нельзя отнести к глобальным, но я хочу рассмотреть их здесь, потому что они могут показать земной шар, то есть своеобразный вид планеты из космоса. Один из них.«Вертикальная проекция близкой перспективы».Вертикальная перспектива крупным планом WKID:54049. Его особенностью является перспективный вид поверхности Земли, как она видится с определенной высоты. На этой проекции хорошо видна высота над эллипсоидом (идеализированная форма, моделирующая Землю).

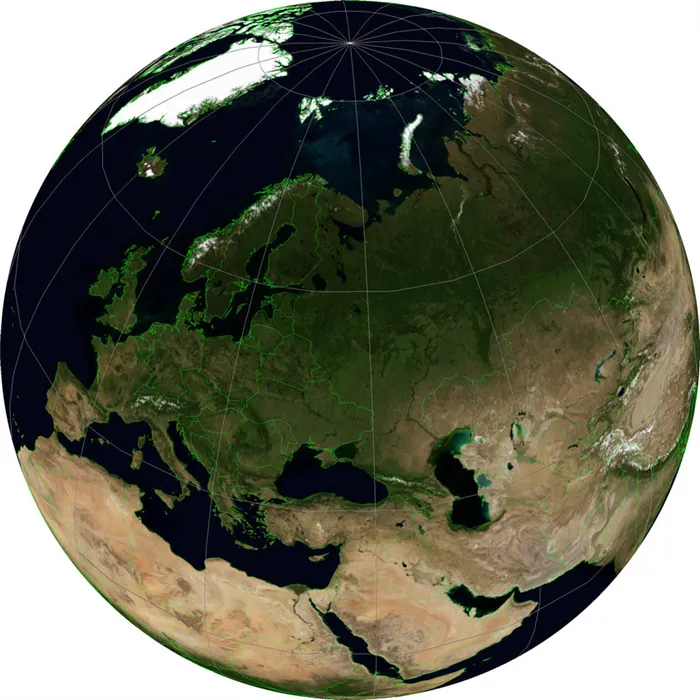
На изображении эта проекция имеет центр широты и долготы, соответствующий широте и долготе Москвы, и высоту 5000000 метров. Чем больше это расстояние, тем больше изображение Земли похоже на изображение в проекции, которую мы рассмотрим в последнюю очередь.

Проекция, которая показывает вид Земли в параллельной перспективе, т.е. как бы с бесконечного расстояния, называется«ортографическая проекция».Ортографическая проекция WKID:43041 PROJ.4:ortho в некотором смысле знакома каждому, кто когда-либо пользовался Google Earth. Я говорю в некотором смысле, потому что «направление взгляда» в этом виде всегда перпендикулярно поверхности Земли, тогда как в Google Earth его можно наклонять по своему усмотрению.

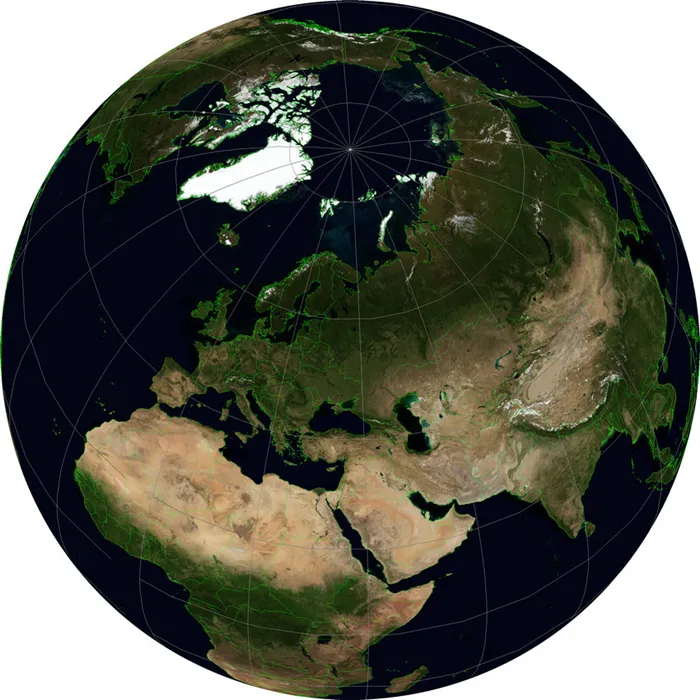
Как и в предыдущем виде, вы можете установить центральную широту и долготу, чтобы выровнять Землю по своему вкусу. Например, можно отобразить полусферу с центром в определенной точке — например, чтобы показать транспортные потоки на континенте, исходящие от одной компании. Создание двух карт с противоположными значениями координат может привести к созданию карты всего мира (хотя искажения по краям будут слишком велики). Создание последовательности карт с плавным изменением центральной точки обеспечивает контекст для движения вращающейся планеты без 3D-графики.

Многие характеристики могут быть измерены независимо от географического положения на поверхности Земли:

Картографические проекции могут быть построены таким образом, что некоторые из этих свойств сохраняются за счет других. Поскольку изогнутая поверхность Земли не является изометричной по отношению к плоскости, сохранение форм неизбежно приводит к изменению масштаба и, следовательно, к непропорциональному представлению поверхностей. И наоборот, проекция, сохраняющая поверхность, может не соответствовать, что приведет к искажению форм и искажению в большинстве мест на карте. Каждая проекция по-разному сохраняет, уравновешивает или приближает основные метрические свойства. Назначение карты определяет, какая проекция положена в основу карты. Поскольку карты служат для различных целей, было разработано множество проекций для этих целей.

Еще одним моментом при настройке проекции является ее совместимость с наборами данных, которые будут использоваться в карте. Наборы данных представляют собой географическую информацию; их охват зависит от выбранного набора данных (модели) Земли. Различные наборы данных дают немного разные координаты в одном и том же месте. Поэтому для крупномасштабных карт, например, карт национальных картографических систем, важно согласовать данные с проекцией. Небольшие различия в отображении координат между разными данными не являются проблемой для карт мира или других крупномасштабных областей, где эти различия ограничены до незаметного уровня.

Искажение

Карл Фридрих Гаусс доказал с помощью теоремы о гравюре, что поверхность сферы не может быть представлена на плоскости без искажений. То же самое относится и к другим опорным поверхностям, используемым в качестве моделей Земли, таким как сплюснутые сфероиды, эллипсоиды и геоиды. Поскольку каждая картографическая проекция является отображением одной из этих поверхностей на плоскости, все картографические проекции деформируются.

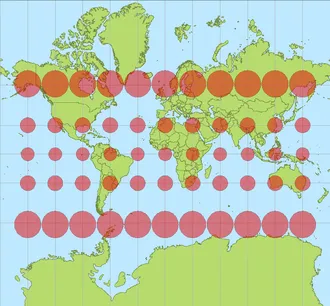
Классическим способом представления деформаций, присущих проекции, является использование таблицы Тиссо. Николя Тиссо описал, как для данной точки, используя масштабный коэффициент k вдоль меридиана, масштабный коэффициент k вдоль параллелей и угол θ ′ между ними, можно построить эллипс, характеризующий величину и ориентацию компонентов деформации. 2 : 147-149 4 Благодаря регулярному расположению эллипсов вдоль долгот и широт, сеть индикаторных линий показывает, как деформация изменяется на карте.

Другие показатели искажения

Описано много других способов определения деформации в проекциях. 5 6 Как и индикаторная матрица Тиссо, индикаторная матрица Гольдберга-Готта основана на бесконечно малых цифрах и показывает изгибные и косые деформации (флексия и косоугольность). 7

Дизайн и конструкция

Создание картографической проекции состоит из двух этапов:

1. Подбор модели по форме Земли или планетного тела (обычно выбирается между сфера или же эллипсоид ). Поскольку фактическая форма Земли неправильная, на этом этапе информация теряется.
2. Преобразование географических координат (долгота и широта ) к Декартово ( Икс, у ) или же полярный плоские координаты. На крупномасштабных картах декартовы координаты обычно имеют простую связь с восток и север определяется как сетка, наложенная на проекцию. На мелкомасштабных картах восточные и северные направления не имеют смысла, и сетки не накладываются друг на друга.

Одними из самых простых картографических проекций являются буквальные проекции, создаваемые путем размещения источника света в определенной точке относительно земного шара и проецирования его деталей на определенную поверхность. Хотя большинство проекций не определяются таким образом, изображение модели сферы источника света может быть полезно для понимания основной концепции картографической проекции.

Выбор проекционной поверхности

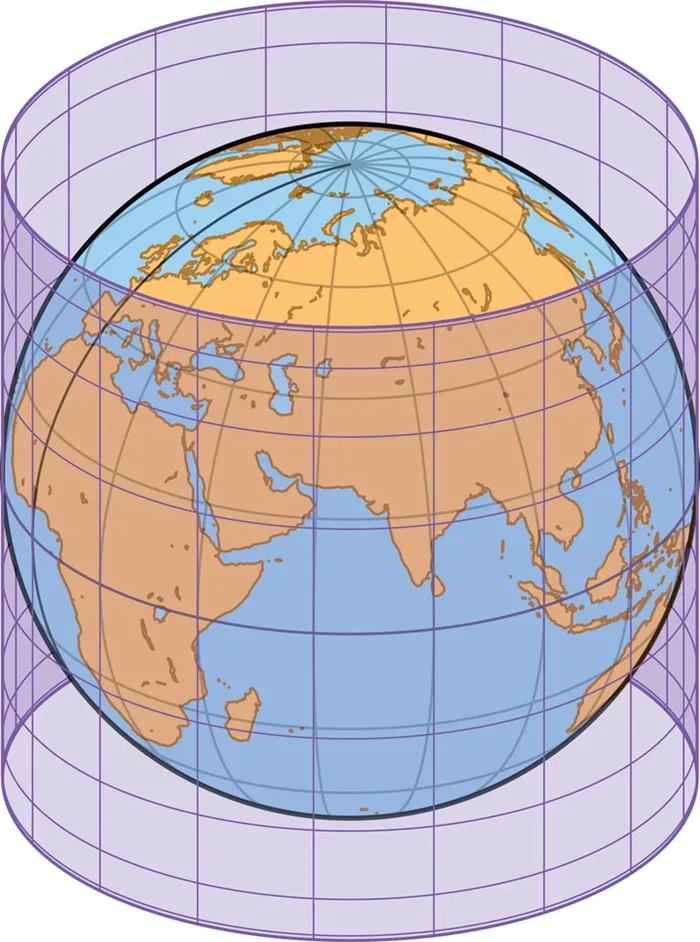
Поверхность, которая может расширяться или разворачиваться в плоскость или лист без растяжения, растрескивания или сжатия, называется разворачивающейся поверхностью. Цилиндр, конус и плоскость являются складчатыми поверхностями. Сфера и эллипсоид не имеют разворачивающихся поверхностей, поэтому любая проекция с них на плоскость должна искажать изображение. (Для сравнения: апельсиновую корку невозможно разгладить без растрескивания и деформации).

Один из способов описать проекцию — это сначала спроецировать с поверхности Земли на развивающуюся поверхность, например, цилиндр или конус, а затем развернуть эту поверхность в плоскость. Хотя первый шаг неизбежно деформирует определенные свойства сферы, развернутая поверхность может быть затем развернута без дальнейшей деформации.

Аспект проекции

Эта поперечная проекция Меркатора математически идентична стандартной проекции Меркатора, но ориентирована вокруг другой оси.

После того как выбор между цилиндрической, конической или плоской проекцией сделан, необходимо определить аспект формы. Аспект описывает, как развернутая поверхность расположена по отношению к глобусу: он может быть нормальным (так, чтобы ось симметрии поверхности совпадала с осью Земли), поперечным (под прямым углом к оси Земли) или косым (под любым углом между ними).

Известные линии

Сравнение тангенциальной и вторичной цилиндрической, конической и азимутальной картографических проекций со стандартными параллелограммами, выделенными красным цветом.

Развернутая поверхность также может быть касательной или вторичной к сфере или эллипсоиду. Тангенциальная означает, что поверхность касается сферы, но не проходит через нее; вторичная означает, что поверхность проходит через сферу. Перемещение разворачивающейся поверхности вне контакта со сферой не сохраняет и не оптимизирует метрические свойства, поэтому эта возможность здесь не рассматривается.

Касательная линия и вторичная линия (стандартные линии) показаны неискаженными. Если эти линии параллельны широте, как в конических проекциях, это называется стандартной параллелью. Центральный меридиан — это меридиан, вокруг которого вращается глобус перед проецированием. Центральный меридиан (обычно λ₀) и параллель начала координат (обычно пишется φ₀) часто используется для определения начальной точки картографической проекции. 16 17

Классификация

Основная классификация проекций основана на типе проекционной поверхности, на которую концептуально проецируется глобус. Проекции описываются гигантской поверхностью, касающейся земли, за которой следует операция неявного масштабирования. Эти поверхности бывают цилиндрическими (например, Меркатора), коническими (например, Альберса) и плоскими (например, стереографическими). Однако многие математические прогнозы не подходят ни под один из этих трех концептуальных методов проектирования. Поэтому в литературе описаны и другие классы сверстников, такие как псевдоконические, псевдоцилиндрические, псевдоасимметричные, ретро-азимутальные и поликонические.

Другой способ классификации проекций основан на свойствах модели, которую они сохраняют. Вот некоторые из наиболее распространенных категорий:

• Сохранение направления ( азимутальный или зенитный ), признак возможен только от одного или двух баллов до любой другой точки. 23
• Сохранение формы локально ( конформный или же ортоморфный )
• Зона сохранения ( равновеликий или же равнозначный или же эквивалент или же аутентичный )
• Сохранение дистанции ( равноудаленный ), признак возможен только между одной или двумя точками и любой другой точкой
• Сохранение кратчайшего пути — черта, сохраняемая только гномоническая проекция

Поскольку сфера не является разворачивающейся поверхностью, невозможно построить одномерную и конформную картографическую проекцию.