Если тело может двигаться в плоскости, например, фигуры на шахматной доске или лодка на озере, то эталонному телу присваивается двумерная система координат.
Слободянюк А.И. Физика 10/2.12
2.12 Относительность движения
Когда мы приводили аргументы в пользу координат, мы подчеркивали, что определение координат имеет смысл только в том случае, если система координат фиксирована, т.е. задана. Поэтому координаты точки являются относительно физическими величинами. Поэтому временные изменения координат также являются относительными, т.е. само механическое движение является относительным 1. Выбор системы координат в принципе произволен и определяется в основном простотой описания или личными предпочтениями исследователя — некоторым людям нравится описывать движение между неподвижными звездами, например. Отсутствие единой, универсальной системы отсчета означает, что все системы отсчета одинаковы; движение в разных системах отсчета должно описываться одинаково. Мы, конечно, не утверждаем, что уравнения движения одинаковы во всех системах отсчета, они будут проще в одних и сложнее в других, но методы описания и результаты должны быть одинаковыми — поэтому если два тела сталкиваются в одной системе отсчета, тот же результат должен существовать в другой системе отсчета. Реально, в природе существуют материальные тела, которые движутся, взаимодействуют и изменяются — и описание движения в определенных системах отсчета является лишь попыткой создать для них более или менее подходящую модель. Корректировка описания движения, переход от одной системы координат к другой, является очень важной физической проблемой, которая выходит далеко за рамки проблем кинематики. В данном разделе мы рассмотрим эту проблему только с точки зрения кинематического описания. Для простоты и облегчения графического представления мы представляем системы координат на плоскости. Обобщение на трехмерное пространство очевидно, и векторная нотация остается той же, более того, мы предполагаем, что соответствующие координатные оси параллельны. Произвольная ориентация координат мало что добавляет к физическому содержанию, а математическое описание становится более громоздким.
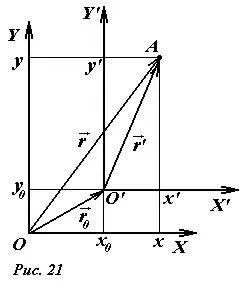
Рассмотрим две системы координат 2: исходную XOY и смещенную X’O’Y’ (рис. 21). Пусть O ‘ обозначает координаты начала смещенной системы координат в исходной системе, а радиус-вектор этой точки \(~\vec r_0\). Связь между координатами материальной точки A в этих системах определяется следующими формулами
\(~Начало x = x_0 + x’ \\\\\ y = y_0 + y’ \end\), (1)
который можно записать в компактной векторной форме
\(~\vec r = \vec r_0 + \vec r\’\). (2)
Эти формулы очевидны для неподвижных систем отсчета и неподвижных тел, теперь нам нужно обобщить их для случая описывающего движения. То есть, нам нужно создать систему отсчета из системы координат, добавив часы в каждую систему координат. У нас по-прежнему нет причин считать, что одни и те же часы идут по-разному в разных системах отсчета. Итак, давайте предположим, что время одинаково в разных системах отсчета и что начало времени также одинаково.
Точка A может двигаться с определенной скоростью \(~\vec \upsilon\ ‘ = \frac\) относительно системы отсчета перемещения. Для определения скорости точки в системе отсчета XOY используется формула (2):
При выводе результатов мы учитывали, что вектор \(~\vec r_0\) постоянна и ее изменение равно нулю. Итак, мы показали, что скорость точки не меняется, когда она переходит из одной фиксированной системы отсчета в другую. Однако этот результат очевиден — ход времени и смещение точек одинаковы в обеих системах отсчета. Если скорости точек не меняются, то не меняются и их ускорения, поэтому они выражаются через изменение скоростей.
Траектория тела различна в разных системах отсчета
Траектория — это относительная характеристика движения. Это связано с тем, что она различна для разных систем отсчета (СО).
Когда самолет летит, точка на конце пропеллера движется по круговой траектории относительно самолета (рис. 1), а относительно неподвижного наблюдателя на земле эта же точка имеет винтообразную траекторию.
Рисунок 1. Траектория движения наконечника винта летящего самолета представляет собой окружность относительно пилота и спиралевидную линию относительно земли.
Например, движение ниппеля велосипеда при езде на велосипеде.
В соответствующей системе отсчета:
- велосипедом, траектория ниппеля – это окружность.
- поверхностью земли, траектория ниппеля – это циклоида.
Что такое циклоида
Циклоида — это плоская изогнутая линия. Точка на окружности движется по такой линии, когда окружность катится по прямой линии без скольжения (рис. 2).
Рисунок 2. Когда окружность катится по прямой линии, точка на окружности описывает окружность
Круговая кривая называется гиперболической кривой.
Линия является трансцендентной, если она не может быть описана алгебраическим уравнением в ортогональных координатах.
Однако мы можем записать x-координату и y-координату отдельно, используя параметр t в этих уравнениях:
\ \big \beginning x = r \cdot t — r \cdot sin(t)\ y = r — r \cdot cos(t)\end \.
Примечания:
- Окружность, которая катится – называется производящей.
- Прямая, по которой катится окружность – направляющая прямая.
- Точки пересечения циклоиды и направляющей прямой – это точки возврата.
- Самые высокие точки на циклоиде, располагающиеся между соседними точками возврата – это вершины циклоиды.
Циклоида была впервые изучена Галилео Галилеем. Этот выдающийся итальянский ученый занимался физикой, математикой, астрономией, техникой и философией.
А английский математик и архитектор Кристофер Рен вычислил длину дуги циклоиды в 1658 году.
Длина циклоиды соответствует четырем диаметрам производственного цикла.
Кристофер Рен спроектировал и руководил строительством купола собора Святого Павла в Лондоне.
С помощью циклоиды братья Бернулли решили проблему быстрого спуска — короткого спуска. Брахистохрон — с греческого означает «короткое время». Они доказали, что шарик катится по трубе в форме перевернутой циклоиды за минимально возможное время.
Скорость тела различна в разных системах отсчета
Рассмотрим движение человека в трамвае, движущемся по прямой линии (рис. 3).
Рисунок 3. Скорость человека по отношению к трамваю составляет 3 километра в час, а по отношению к земле — 63 километра в час.
Скорость трамвая \(\large \vec>>\) 60 километров в час. Предположим, в движущемся вагоне трамвая человек перемещается от задней части трамвая к его передней части, со скоростью \(\large \vec>>\) 3 километра в час.
Тогда скорость человека относительно трамвая составляет 3 километра в час, а относительно земли — 63 километра в час.
Как переходить из одной системы отсчета в другую
Каждое рассматриваемое нами движение, а также его свойства различны в разных системах отсчета.
По отношению к одним телам рассматриваемое тело может находиться в состоянии покоя, а по отношению к другим телам — в движении.
Чтобы осуществить переход между системами отсчета, мы должны применить закон сложения скоростей и перемещений. Скорость и перемещение — это векторы. Поэтому мы будем складывать их геометрически. То есть, когда мы складываем векторы, мы будем учитывать их направления.
Примечание: Ньютон изучал движение тел. Согласно его теории, время движется с одинаковой скоростью во всех системах отсчета. То есть, в ньютоновской механике время является абсолютной величиной.
Представьте себе следующую картину: Девушка сидит на берегу реки и отдыхает (рис. 4). Мимо нее по реке (вниз по течению) проплывает плот. Молодой человек спрыгивает с плота и переплывает на другой берег реки. Затем он садится на берег и отдыхает.
Рисунок 4. Чтобы найти скорость пловца относительно неподвижного наблюдателя, сложите вектор скорости реки и вектор скорости самого пловца.
Перемещение в различных системах отсчета
Давайте сначала запишем перемещение мужчины в системе отсчета, связанной с девушкой, если нам известно его перемещение в системе отсчета, связанной с плотом.
Примечание:
- Относительно девушки – значит, в системе отсчета, связанной с девушкой.
- Относительно плота – значит, в системе отсчета, связанной с плотом.
На рисунке движение плота и движение мальчика относительно плота обозначены длинными черными стрелками. А движение мальчика относительно девочки, сидящей на скамейке, обозначено длинной синей стрелкой.
На рисунке показано, что векторы смещения образуют прямоугольный треугольник.
Сложение вектора смещения и вектора относительного смещения дает вектор абсолютного смещения:
\( \large \overrightarrow>>\) — вектор смещения плота,
\( \large \overrightarrow>>\) — вектор смещения опорной части относительно плота (смещение самой опорной части),
\( \large \overrightarrow>>\) — вектор движения мужчины по отношению к девушке на скамейке,
Длина вектора абсолютного смещения может быть определена по теореме Пифагора:
Скорость в различных системах отсчета
Перепишем формулу для отношения смещения:
Если мы знаем перемещение и время равномерного движения, мы можем найти меру вектора скорости, т.е. длину вектора скорости.
Скорость плавучего плота и скорость человека не меняются. Поэтому, чтобы связать скорость и перемещение, мы можем использовать следующую формулу
\ \ большой S = v \cdot t \
Если мы разделим обе части этого уравнения на время t, то получим выражение для скорости равномерного движения:
Разделите обе части уравнения для перемещения на время t движения.
Полученное выражение можно записать с помощью векторов скорости:
На рисунке 4 красные векторы обозначают скорость реки (плота) и скорость человека.
Опишем обозначения, которые мы использовали в уравнении, связывающем скорости в разных системах отсчета:
\( \large \overrightarrow>>= \overrightarrow>>\) — вектор скорости формулы,
\( \large \overrightarrow>>= \overrightarrow>>\) — вектор скорости плота (речного потока),
\( \large \overrightarrow>>\) — вектор скорости мужчины по отношению к девушке,








