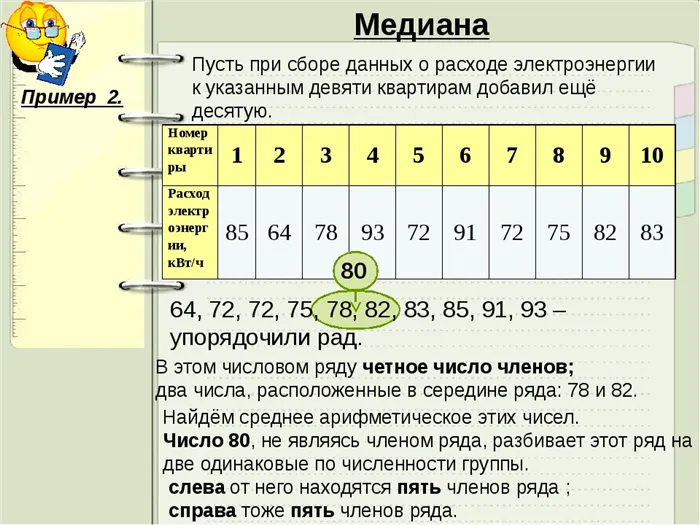
Это первый вариант, если данные имеют центральное значение. Второй вариант — когда данные имеют номер Весов. Это означает, что существует два центральных значения вместо одного. Решение простое: берется среднее арифметическое двух центральных значений.
Математическая статистика — основы
Слово «статистика» происходит от латинского «status», что означает «состояние и положение вещей».
Статистика занимается изучением количественных аспектов большого числа общественных явлений и процессов в арифметической форме, выявляя конкретные критерии.
Сегодня статистика используется практически во всех областях общественной жизни, от моды, кулинарии и садоводства до астрономии, экономики и медицины.
Первое, что нужно знать о статистике, — это найти основные статистические характеристики, используемые для анализа данных.
Математическая статистика — коротко о главном
Определение математической статистики:.
Статистическая выборка — это определенное количество объектов, отобранных по общему количеству исследуемых объектов.
Объем выборки определяется как количество \(_>, _>, \ …, Ј _> \) элементов в выборке.
Вариабельность выборки — это разница между максимальным и минимальным значениями элементов выборки.
Среднее число набора чисел представляет собой отношение этих чисел, деленное на количество (объем выборки).
Среднее арифметическое набора чисел \(_> \ справа)\ — это коэффициент суммы этих чисел (\ слева (_>+_> … +_> \ право).
Метод серии чисел — наиболее часто встречающееся число в этой последовательности.
Медиана ряда упорядоченных чисел с ненулевым числом членов является медианным числом.
Медиана ряда упорядоченных чисел со значительным числом членов — это среднее арифметическое двух чисел, описанных в середине.
Частота — это количество повторений. То есть количество раз, когда за определенный период времени произошло событие, объект или определенное свойство наблюдаемого параметра достигло определенного значения.
Частота — это количество повторений конкретного значения параметра в выборке.
Частота — это отношение частоты к общему количеству данных в серии.
Для наглядности рекомендуется представить данные в виде соответствующей диаграммы/буквы.
Статистические характеристики
Основными статистическими характеристиками выборки данных являются…
Под «выборкой» мы понимаем данные, подлежащие изучению.
Следующий пример поясняет это.
Таким образом, основные статистические характеристики выборки данных включают.
- объем выборки,
- размах выборки,
- среднее арифметическое,
- мода,
- медиана,
- частота,
- относительная частота.
Вау, вау, вау, вау! Это много новых слов! Давайте рассмотрим их по очереди.
Объем и размах выборки
Образцом является соответствующий элемент \(_>, _>, \ …, ˈ _> \). Количество этих элементов ⌘ (⌘ слева (n ⌘ справа) ⌘) называется объемом образца.
Например, в следующей таблице приведены данные о росте игроков национальной футбольной команды.

Этот образец основан на элементах ⌘ (⌘ displaystyle 11 \) ᤩ (⌘ displaystyle \ left (_> = 183; \ _> = 194; \ _> = 187; \ … \ _> = 181 \ справа) представлена. \(_> = 181).
Таким образом, размер выборки ˉ (ˉ displaystyle \ left (n \ right) ˉ) составляет ˉ (ˉ displaystyle 11 \).
Разница между максимальным и минимальным элементами выборки называется дисперсией выборки.
Выборка разброса определяется как ⌘(_)<\max >> -_<\min >> = 194-176 = 18 \) см.
Среднее арифметическое выборки
Среднее арифметическое набора чисел \(__> \ справа)\ — это коэффициент, который делит сумму этих чисел \(__> слева (_>+_> … +_> \ справа). Эти числа (\left (n \ справа).
Непонятно: квантор — это квантор квантора, который делит сумму чисел. Давайте рассмотрим наш пример.
Определите средний рост игрока.
Продолжить; \ (\ displaystyle _> = 183; \ _> = 194; \ _> = 187; \ … ; \ _> = 181 \) \ (⌘ displaystyle n = 11 \).
Все можно отнести к типу: …
Таким образом, средний рост игрока национальной сборной составляет ⌘ (⌘ displaystyle 183,8 \) см.
Или вот такой пример:.
Учащимся 9 класса была дана неделя на то, чтобы решить как можно больше примеров из задачника. Ниже показано количество примеров, решаемых студентами в неделю.
Найдите среднее количество решенных задач.
Таблица содержит данные по студентам в ዄ (ዄ displaystyle 20 \). поэтому \(ᢙ displaystyle n = 20 \). )
Теперь найдите сумму (общее количество) всех задач, решенных первыми 20 студентами.
Теперь можно смело переходить к вычислению среднего арифметического решенных задач.
Таким образом, в среднем учащиеся 9-го класса решали задачи с ⌘ (displaystyle 78 \).
Другой пример:.
На рынке помидоры продаются продавцом \(displaystyle 7 \) и цены распределяются следующим образом\(displaystyle 1 \) Цена за килограмм (рубль): {\(displaystyle 60, \ text< >55, {text< >54, {text< >70, {text< >65, {text< >67, {text< >(63 {text).
Какова средняя цена килограмма помидоров на рынке?
Частота — это количество повторений. То есть количество раз, когда за определенный период времени произошло событие, объект или определенное свойство наблюдаемого параметра достигло определенного значения.
Постановка задачи
Входом в алгоритм является поток целых чисел. Это означает, что количество чисел может быть неизвестно, но предполагает, что таблица заранее определена и ее длина очень велика. Необходимо разработать алгоритм для определения медианного значения текущей таблицы, т.е. того, что было прочитано в исходной таблице в данный момент времени. Сложность такого алгоритма составляет
Давайте начнем с некоторых основных понятий. Медиана — это число, находящееся в середине последовательности чисел. Например, в ряду: 1, 2, 3, 7, 9, 3 является медианой. Если количество чисел представляет собой шкалу, медиана — это среднее значение двух медианных чисел.
В качестве альтернативы, если пронумерованный элемент является ярмом, можно выбрать один корпус.
Наивный подход
Давайте обсудим основные решения, которые могут привести к медиане.
Введем каждое новое число в таблицу из Flow так, чтобы таблица оставалась отсортированной. Затем выберите элемент с пояса и добавьте его в список носителей.
Как упоминалось выше, этот алгоритм имеет квадратичную сложность. Это происходит потому, что для каждого элемента в потоке он выполняет линейную задачу нахождения позиции и импорта элемента в таблице.
Для улучшения этого эффекта можно использовать структуру данных — кучу.
Куча. Min-heap, max-heap
В качестве примера рассмотрим пакет, использующий Minheap. Мини-куча — это двоичное дерево со следующими двумя свойствами: минимальная емкость двоичного дерева определяется как количество байтов в двоичном дереве.
- ключи любого узла этого дерева всегда меньше, чем ключи его двух дочерних узлов,
- такое дерево является полным, т.е. у него должны быть заполнены все уровни, за исключением последнего.
Максимальная мощность определяется аналогичным образом и должна быть заменена первым свойством «меньше» и «больше». При решении задачи мы хотим использовать возможность работать быстрее линейного времени, создавая кучи.
Первая из этих операций: взятие минимума (максимума) и удаление
Используя сваю, функция минимального приема может выполняться в фиксированное время. Минимумы всегда хранятся в корне дерева, что облегчает поиск цен. Если вы хотите удалить минимум и сразу же заменить его более высоким элементом, вам нужно вызвать метод извлечения, временная сложность которого также не равна линейной.
Метод экстракции запускает следующие шаги изнутри. Сначала элементы размещаются с самого последнего уровня корня дерева, затем метод bubble_down начинается с корня дерева и идет от уровня к уровню (и в полном дереве). Новый корень узла опускается. Смотрите код реализации на языке Python ниже.
Вторая операция: добавление элемента
Чтобы добавить любой элемент в кучу, новый элемент должен быть помещен в правильное положение без потери двух свойств кучи. Для этого новый элемент добавляется к последнему уровню, а затем используется метод bubble_up для подъема по маршруту, пока элемент над ним не станет меньше или маршрут не будет завершен. Существует также сложность этой функции
Код для определения функциональности, необходимой для определения MIN и MAX HEAP:.
Вернитесь к примеру с игроком. Была рассчитана частота каждого значения. Мы также знаем общее количество данных в строке (⌘Left (n = 11 \Right)⌘).
Медиана набора чисел это — что такое медиана набора чисел? и как найти медиану 13, 19, 24, 17, 15, 11. — 22 ответа
Медиана чисел как найти
Как найти медиану набора чисел и медиану 13, 19, 24, 17, 15 и 11 для удаленной работы. Автор дал лучший ответ: медиана набора чисел — это число, которое делит целое на две равные части. Вместо «медиана» мы можем сказать. 1. числа должны быть записаны в порядке возрастания (образуют порядок ранжирования) 11,13,15,17,19,24 2. одновременно удаляйте «наибольшее» и «наименьшее» число конкретного числа, пока не останется одно или два числа. 3. если остается число, то это медианное число. 4. если остаются два числа, медиана — это среднее арифметическое двух оставшихся чисел. Я = 15+17/2 = 16
Ответ ведущего эксперта по ответу 22.
Здравствуйте! Здесь собраны темы с ответами на ваш вопрос: что такое медиана набора чисел? Как найти медиану из 13, 19, 24, 17, 15 и 11.
В ответах Pososhok Active они расположены в порядке возрастания. Тот, который находится посередине, является медианой. (Если их много (как в вашем случае), медиана будет средним числом двух средних чисел. 11, 13, 15, 17, 19, 24 (15+17)/2 = 16.
Ответы пользователя будут удалены Специалисты помещают число в ряд, а в середине ряда будет «медиана». Обычно дает один номер…
Ответ 2 от первого пользователя ответа
Здравствуйте! Следующий вопрос, касающийся правильного ответа, звучит следующим образом.
Подмножество проблем в Википедии, см. статью Википедии о подмножестве проблем в суммах
Медиана статистики Википедии, см. медиана статистики Википедии
Медь в Википедии
Ответить на вопрос:
Подскажите пожалуйста. А как находят медиану? ( по алгебре)
Описывает числовую последовательность цифр, удаляя цифры с краев, пока не останется только одна. Если это медиана и осталось два числовых значения, найдите среднее число. 2,2,3,5,6,7,10,12 2,2,3,5,6,7,10,10,10 2,3,5,6,7,10 2,3,5,6,7,10 3.5,6,7 5.6 У нас осталось два числа, находим числовое среднее (5+6)/2 = 5.5 — должна быть пирамида.

AO — это медиана, противоположная середине.
Если вам нужна геометрическая медиана, то первый ответ — первый, но если вам нужна алгебраическая медиана, то среднее число — это медиана, в порядке возрастания: 4 3 8 6 5, в порядке возрастания 345 6 8 Медиана равна 5. Если чисел четное количество, медиана — это среднее арифметическое среднего числа: 4 3 8 5. Здесь, в порядке возрастания 3 4 5 8, мы получаем два числа в середине и ищем среднее арифметическое. (4 + 5) / 2 = 4,5, а медиана равна 4,5.
Статистика занимается изучением количественных аспектов большого числа общественных явлений и процессов в арифметической форме, выявляя конкретные критерии.
Квартили, децили, перцентили
Аналогично можно найти значение точки в любой отсортированной единице ранжированного ряда, найдя его из ряда вариаций распределения. Например, вы можете найти значение атрибута в единицах, которые делят последовательность на четыре равные части, десять частей или 100 частей. Эти значения называются «квадратами», «децималами» или «сотыми». Квадранты — это характерные значения, которые делят классифицированную совокупность на четыре равные части. Нижний квадрант (Q1) — это четверть населения с наименьшим значением характеристики, а верхний квадрант (Q3) Это пересекается с 1/4 отрезка с наибольшим значением характеристики. Это означает, что 25% единиц населения будут иметь более низкое значение Q125% единиц будут находиться между Q1 и Q2; 25% будет находиться между Q2 и Q3Остальные 25% будут выше Q3Q ; 25% единиц будут находиться между Q и Q ; 25% будут находиться между Q и Q Средний квадрант Q2 Медиана. Формула используется для вычисления квадранта ряда пространственных вариаций Где xQ1 — нижняя граница интервала, содержащегося в нижнем квадранте (интервал определяется кумулятивной частотой, впервые превышающей 25%) — xQ3 — является нижней границей интервала, включенного в верхний квадрант (интервал определяется по первой суммарной частоте, превышающей 75%) — i — значение диапазона — SQ1-1 -Суммарная частота интервала, предшествующего интервалу, содержащему нижний квадрант-SQ3-1 -Суммарная частота интервала, предшествующего интервалу, содержащему верхний квадрант — fQ1 Частота интервала, содержащего нижний квадрант — fQ3 Частота интервала, содержащего верхний квадрант. Используя данные таблицы 10, рассмотрим расчеты для нижнего и верхнего квадрантов. Нижний квадрант лежит в диапазоне 60-80 и имеет кумулятивную частоту 33,5%. Верхний квадрант лежит в диапазоне 160-180 и имеет кумулятивную частоту 75,8%. Исходя из этого, делается следующее
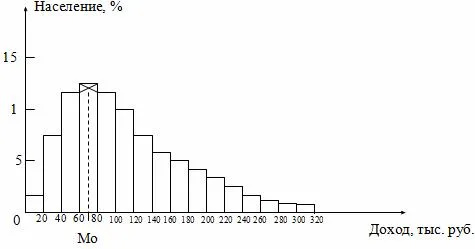
В дополнение к квадрантам, десятичные числа (варианты, которые делят упорядоченный ряд изменений на 10 равных частей) могут быть определены в последовательности переменных. Первая десятичная дробь (d1) делит население на отношение 1/10 к 9/10 с точностью до второго десятичного знака (d1) — в соотношении 2/10 к 8/10 и т.д. Рассчитывается по следующей формуле:,. Значение признака, которое делит ряд на 100 частей, называется процентилем. Медиана, квадратичное, десятичное и перцентильное соотношения показаны на рисунке 5.5.
В данной статье рассматриваемый пример был использован для иллюстрации преимуществ свай по сравнению со списками. Мы узнали о временной сложности операций в этой структуре данных. Мы реализовали код, необходимый для эффективного выполнения задач промежуточного поиска в потоке чисел.
Медиана ряда чисел, 7 класс
Федеральный закон N273-ФЗ «Об образовании в Российской Федерации» обращает внимание на то, что в организациях, осуществляющих образовательную деятельность, воспитание и обучение обучающихся с ограниченными возможностями здоровья организуется совместно с другими обучающимися. В отдельных классах или группах.


Курсы повышения квалификации.

Основные статистические характеристики 21.10.2019 Муниципальное общеобразовательное учреждение Гимназия № 15 г. Ореховожево Московской области МОУ Гимназия учителей математики № 15СаухинаЕвгения Олеговна

Основные статистические свойстваЦель: ввести понятие медианы как статистического свойства упорядоченного ряда — разработать функцию нахождения медианы четного и нечетного упорядоченного ряда.

Статистические характеристики: среднее арифметическое, диапазон, мода, медиана. 2 1 4 3

Среднее арифметическое набора повторяющихся чисел — это коэффициент суммы этих чисел, деленный на количество их слагаемых. Диапазон чисел — это разница между самым большим и самым маленьким числом. Метод числовой последовательности — это число, которое чаще всего встречается в последовательности.

Устная работа Дан упорядоченный ряд: 1; 1; 4; 5; 6; 7. Найдите: a) среднее арифметическое ряда — b) дисперсию ряда — c) моду ряда.

Вербальный рабочий порядок: 1; 1; 4; 5; 6; 7. Найдите: a) среднее арифметическое ряда — b) ширину ряда — c) коэффициент ряда. Ответ: a) 4; b) 6; c) 1.

Как и среднее арифметическое, оно показывает, где каждый набор чисел находится на числовой прямой и где их центр. Другим показателем является медиана. Медиан происходит от латинского mediana, что означает «средний». Вместо «посередине» мы можем сказать «в середине». Медиана набора чисел — это число, которое делит набор на две равные части. Описание нового материала
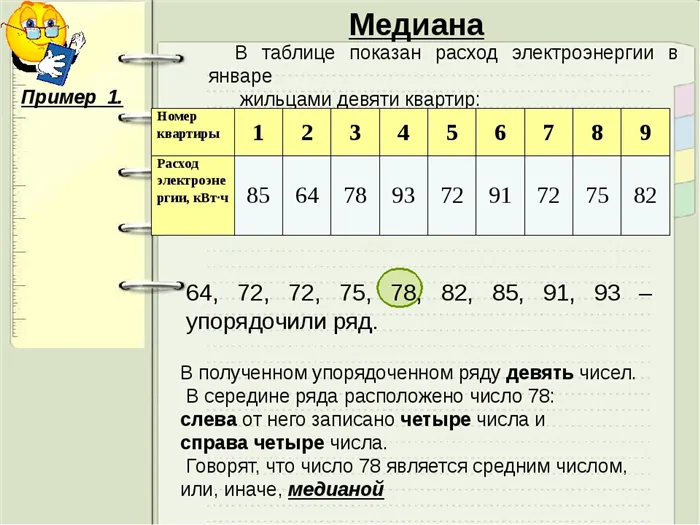
В средней таблице показано потребление электроэнергии в январе жильцами девяти квартир — 64, 72, 72, 75, 78, 82, 85, 91 и 93. В полученной последовательности девять чисел. В середине ряда находится число 78. На левой стороне — четыре числа, на правой — четыре числа. Число 78 называют медианой или медианным значением. Номер квартиры 123 4 5 6 7 8 9 Потребление электроэнергии, кВт/ч 85 64 78 93 72 91 72 75 82